ความถนัดแพทย์ MEDDENT
เข้าสู่ระบบ
ปรึกษาแอดมิน
จำนวนเชิงซ้อน

จำนวนเชิงซ้อน

ตุลาคม 11, 2025

เลือกดูตามหัวข้อได้ครับ
จำนวนเชิงซ้อน
การดำเนินการของจำนวนเชิงซ้อน
กราฟของจำนวนเชิงซ้อน
จำนวนเชิงซ้อนในรูปเชิงขั้ว

สวัสดีค้าบบ ในตอนนี้พี่แม็คจะให้น้อง ๆ มาทำความรู้จักกับจำนวนชนิดใหม่ นั่นคือ จำนวนเชิงซ้อนนะครับ ซึ่งพี่แม็คจะมาสรุปเนื้อหาสาระสำคัญที่เกี่ยวข้องกับจำนวนเชิงซ้อนให้น้องฟังกันคร่าว ๆ ดังนี้ค้าบบ ^^

จำนวนเชิงซ้อน

ก่อนอื่นพี่แม็คจะให้พิจารณาสมการ x2+1=0x^2 + 1 = 0 ซึ่งจะเห็นว่า คำตอบของสมการจะไม่สามารถหาได้ เพราะว่าไม่มีจำนวนจริงใด ๆ ที่ยกกำลัง 2 แล้วมีค่าเท่ากับ −1-1 โดยการหาคำตอบจะนิยามจำนวนชนิดใหม่ คือ จำนวนเชิงซ้อน และกำหนดให้ i2=−1i^2 = -1 โดย ii เป็นหน่วยจินตภาพ จากสมการ x2+1=0x^2 + 1 = 0 จะได้สมการ x2−(−1)=0x^2 - (-1) = 0
นั่นคือ x2−i2=0x^2 - i^2 = 0 ทำให้ (x−i)(x+i)=0(x-i)(x+i) = 0 ดังนั้น คำตอบของสมการคือ x=ix=i และ x=−ix=-i

จำนวนเชิงซ้อน (complex number) คือ จำนวนที่เขียนอยู่ในรูปของ a+bia+bi หรือ (a,b)(a,b) เมื่อ a,ba,b เป็นจำนวนจริง
โดยทั่วไปแล้วจำนวนเชิงซ้อนมักจะเขียนแทนด้วย z,wz,w

ในที่นี้จำนวนเชิงซ้อน z=a+biz=a+bi หรือ z=(a,b)z=(a,b) จะประกอบไปด้วย 2 ส่วนที่สำคัญ นั่นคือ
1. ส่วนจริง (real part) ของ zz คือ จำนวนจริง aa จะเขียนแทนด้วย Re(z)=a\mathrm{Re}(z) = a
2. ส่วนจินตภาพ (imaginary part) ของ zz คือ จำนวนจริง bb จะเขียนแทนด้วย Im(z)=b\mathrm{Im}(z) = b

การดำเนินการของจำนวนเชิงซ้อน

ให้ z=a+biz=a+bi และ w=c+diw=c+di เป็นจำนวนเชิงซ้อน
การบวก: z+w=(a+bi)+(c+di)=(a+c)+(b+d)iz+w=(a+bi)+(c+di) = (a+c) + (b+d)i
TIPS: ให้น้องนำส่วนจริงมาบวกกัน และส่วนจินตภาพบวกกัน

การคูณ: zw=(a+bi)(c+di)=ac+adi+bci+bdi2=(ac−bd)+(ad+bc)izw=(a+bi)(c+di) = ac + adi + bci + bdi^2 = (ac-bd) + (ad + bc)i
TIPS: ให้น้อง ๆ ทำแบบคูณกระจาย แต่อาจจะต้องระวังเครื่องหมายด้วยนะครับ เพราะในเทอมสุดท้ายจะมี i2i^2 ซึ่งจะมีค่าเท่ากับ −1-1 ทำให้เครื่องหมายเปลี่ยนครับ และเป็นจุดที่น้องๆ สามารถพลาดได้ง่ายครับ

Ex. กำหนดให้ z=1+2iz=1+2i และ w=3−4iw=3-4i จงหาค่าของ z+wz+w และ zwzw
วิธีทำ

z+w=(1+2i)+(3−4i)=(1+3)+(2−4)i=4−2i \begin{align*} z+w &= (1+2i)+(3-4i) \\ &= (1+3) + (2-4)i \\ &= 4-2i \end{align*}

และ

zw=(1+2i)(3−4i)=3−4i+6i−8i2=3−4i+6i−8(−1)=(3+8)+(−4+6)i=11+2i \begin{align*} zw &= (1+2i)(3-4i) \\ &= 3-4i+6i-8i^2 \\ &= 3-4i+6i-8(-1) \\ &= (3+8)+(-4+6)i \\ &= 11+2i \end{align*}

Post

ให้ z=a+biz=a+bi และ w=c+diw=c+di เป็นจำนวนเชิงซ้อน
ตัวผกผันภายใต้การบวกของจำนวนเชิงซ้อน z=a+biz=a+bi เขียนแทนด้วย −z-z คือ −z=−a−bi-z=-a-bi
การลบ: z−w=z+(−w)=(a+bi)+(−c−di)=(a−c)+(b−d)iz-w = z+(-w)=(a+bi)+(-c-di) = (a-c) + (b-d)i
TIPS: ให้น้องนำส่วนจริงมาลบกัน และส่วนจินตภาพลบกัน

Ex. กำหนดให้ z=1+2iz=1+2i และ w=3−4iw=3-4i จงหาค่าของ z−wz-w
วิธีทำ

z−w=(1+2i)−(3−4i)=(1−3)+(2+4)i=−2+6i \begin{align*} z-w &= (1+2i)-(3-4i) \\ &= (1-3) + (2+4)i \\ &= -2+6i \end{align*}

ตัวผกผันภายใต้การคูณของจำนวนเชิงซ้อน z=a+biz=a+bi เมื่อ z≠0z \neq 0
เขียนแทนด้วย z−1z^{-1} คือ z−1=aa2+b2−ba2+b2iz^{-1}=\displaystyle \frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i

การหาร: z÷w=zw−1z \div w = zw^{-1} และเขียนแทน z÷wz \div w ด้วย zw\displaystyle\frac{z}{w}
TIPS: การหารของจำนวนเชิงซ้อน น้อง ๆ สามารถทำได้ 2 วิธีดังนี้
วิธีที่ 1 ใช้ตัวผกผันการคูณ
จาก zw−1=(a+bi)(cc2+d2−dc2+d2i)=ac+bdc2+d2+(bc−adc2+d2i)zw^{-1} = (a+bi)\left(\displaystyle \frac{c}{c^2+d^2}-\frac{d}{c^2+d^2}i\right) = \displaystyle\frac{ac+bd}{c^2+d^2}+\left(\displaystyle\frac{bc-ad}{c^2+d^2}i\right)

Ex. กำหนดให้ z=1+2iz=1+2i และ w=3−4iw=3-4i จงหาค่าของ zw\displaystyle\frac{z}{w}
วิธีทำ

zw=(1+2i)(332+(−4)2−(−4)32+(−4)2i)=(1+2i)(325+425i)=325+425i+625i+825i2=(325−825)+(425+625)i=−525+1025i=−15+25i \begin{align*} \displaystyle\frac{z}{w} &= (1+2i)\left(\displaystyle\frac{3}{3^2+(-4)^2}-\frac{(-4)}{3^2+(-4)^2}i\right) \\ &= (1+2i)\left(\displaystyle\frac{3}{25}+\frac{4}{25}i\right) \\ &= \displaystyle\frac{3}{25}+\frac{4}{25}i + \displaystyle\frac{6}{25}i+\frac{8}{25}i^2 \\ &= \left(\displaystyle\frac{3}{25} -\frac{8}{25}\right) +\left(\frac{4}{25} + \displaystyle\frac{6}{25}\right)i\\ &= -\displaystyle\frac{5}{25} +\frac{10}{25}i \\ &= -\displaystyle\frac{1}{5} +\frac{2}{5}i \end{align*}

วิธีที่ 2 ใช้สังยุคของตัวหาร
สังยุค (conjugate) ของจำนวนเชิงซ้อน z=a+biz=a+bi เขียนแทนด้วย zˉ\bar{z} คือ zˉ=a−bi\bar{z} = a-bi

Ex. กำหนดให้ z=1+2iz=1+2i และ w=3−4iw=3-4i จงหาค่าของ zw\displaystyle\frac{z}{w} โดยใช้สังยุคของตัวหาร
วิธีทำ เนื่องจาก w=3−4iw=3-4i จะได้ว่า wˉ=3+4i\bar{w}=3+4i ทำให้

zw=(1+2i3−4i)(3+4i3+4i)=3+4i+6i+8i232+12i−12i−16i2=(3−8)+(4+6)i9+16=−5+10i25=−525+1025i=−15+25i \begin{align*} \displaystyle\frac{z}{w} &= \left(\displaystyle\frac{1+2i}{3-4i}\right)\left(\displaystyle\frac{3+4i}{3+4i}\right) \\ &= \displaystyle\frac{3+4i+6i+8i^2}{3^2+12i-12i-16i^2} \\ &= \displaystyle\frac{(3-8)+(4+6)i}{9+16} \\ &= \displaystyle\frac{-5+10i}{25}\\ &= -\displaystyle\frac{5}{25} +\frac{10}{25}i \\ &= -\displaystyle\frac{1}{5} +\frac{2}{5}i \end{align*}

ค่าสัมบูรณ์ (absolute value, modulus) ของจำนวนเชิงซ้อน z=a+biz=a+bi เขียนแทนด้วย ∣z∣=a2+b2\left|z\right| = \sqrt{a^2+b^2}

Ex. กำหนดให้ z=1+2iz=1+2i และ w=3−4iw=3-4i
จงหา ∣z∣\left|z\right| และ ∣w∣\left|w\right|
วิธีทำ
เนื่องจาก z=1+2iz=1+2i จะได้ว่า ∣z∣=12+22=1+4=5\left|z\right| = \sqrt{1^2+2^2}=\sqrt{1+4} =\sqrt{5}
และจาก w=3−4iw=3-4i จะได้ว่า ∣w∣=32+(−4)2=9+16=25=5\left|w\right| = \sqrt{3^2+(-4)^2}=\sqrt{9+16} =\sqrt{25}=5

กราฟของจำนวนเชิงซ้อน

ก่อนอื่นพี่แม็คจะให้น้อง ๆ ทำความรู้จักกับกราฟของจำนวนเชิงซ้อน ดังนี้

Post

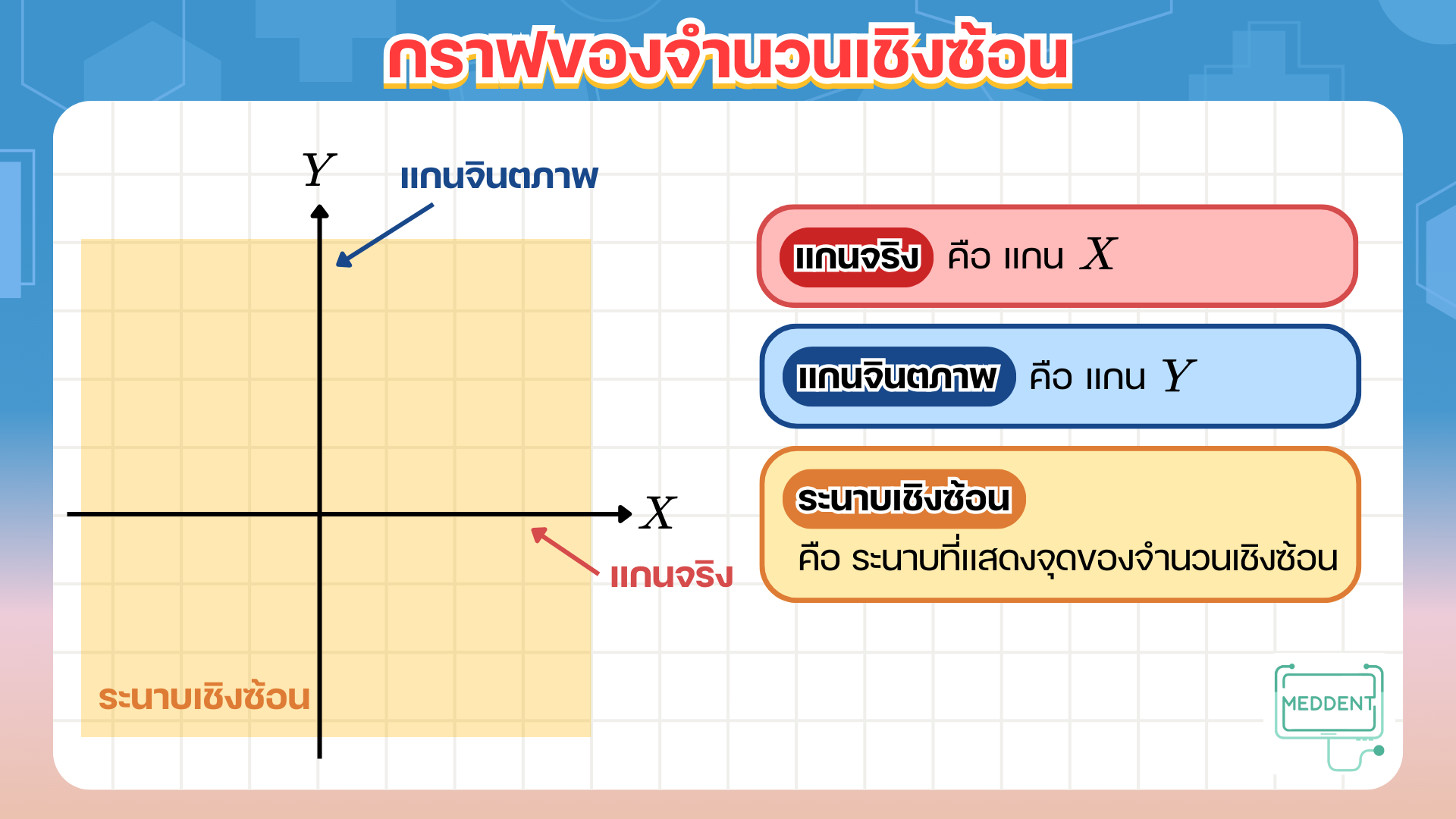
เนื่องจากจำนวนเชิงซ้อนอย่างที่พี่แม็คพูดถึงในตอนแรกจะสามารถเขียนได้ 2 แบบ นั่นคือ a+bia+bi หรือคู่อันดับ (a,b)(a,b) โดยที่ aa และ bb เป็นจำนวนจริง ซึ่งจำนวนเชิงซ้อนสามารถแสดงได้บนระนาบเชิงซ้อน ดังนี้ค้าบบ

Post

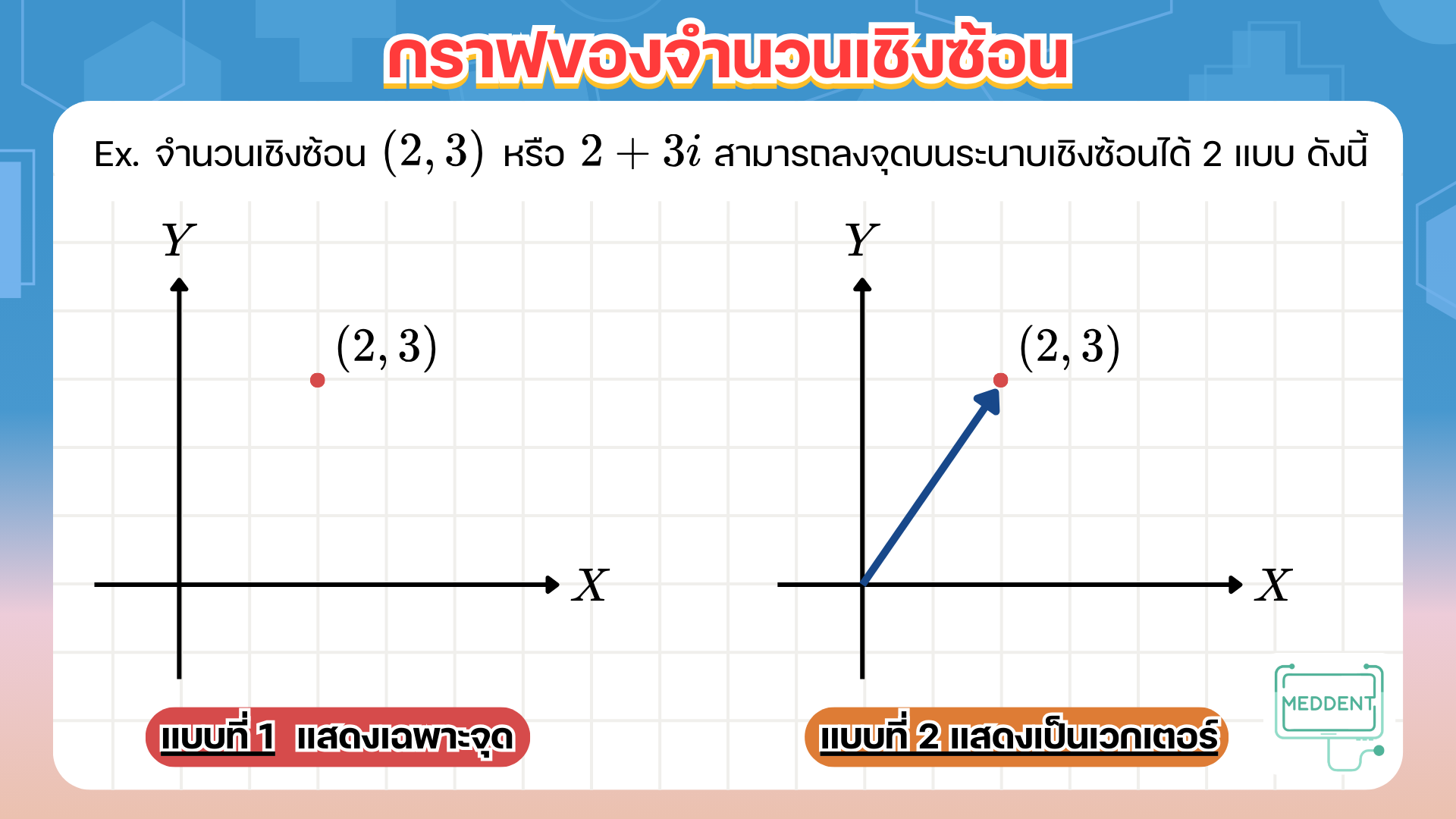
จำนวนเชิงซ้อน 2+3i2+3i สามารถเขียนแทนแสดงได้ 2 แบบคือ
แบบที่ 1 แสดงเฉพาะจุด นั่นคือ จุด (2,3)(2,3) บนระนาบเชิงซ้อน
แบบที่ 2 แสดงเป็นเวกเตอร์ นั่นคือ เวกเตอร์ที่มีจุดเริ่มต้นอยู่ที่จุด (0,0)(0,0) และจุดสิ้นสุดอยู่ที่จุด (2,3)(2,3)

ก่อนอื่นพี่แม็คจะทบทวนการหาระหว่างจุดสองจุด ดังนี้
ถ้าเกิดว่าน้อง ๆ ต้องการหาระยะห่างระหว่างจุด P(a,b)P(a,b) และ Q(c,d)Q(c,d) จะได้ว่าระยะห่างระหว่างจุด PP และ QQ เท่ากับ ∣PQ‾∣=(a−c)2+(b−d)2\left|\overline{PQ}\right| = \sqrt{(a-c)^2+(b-d)^2} หน่วย
Ex. กำหนดให้ P(1,2)P(1,2) และ Q(3,−4)Q(3,-4)
จะได้ว่า ∣PQ‾∣=(1−3)2+(2−(−4))2=(−2)2+(6)2=4+36=40\left|\overline{PQ}\right| = \sqrt{(1-3)^2+\big(2-(-4)\big)^2} = \sqrt{(-2)^2+(6)^2} = \sqrt{4+36} = \sqrt{40} หน่วย

กำหนดให้ z1=a+biz_1 = a+bi และ z2=c+diz_2 =c+di
จะได้ว่า ∣z1−z2∣=(a−c)2+(b−d)2\left| z_1 - z_2 \right| = \sqrt{(a-c)^2+(b-d)^2} จะเป็นระยะห่างระหว่างจุดสองจุด z1z_1 และ z2z_2

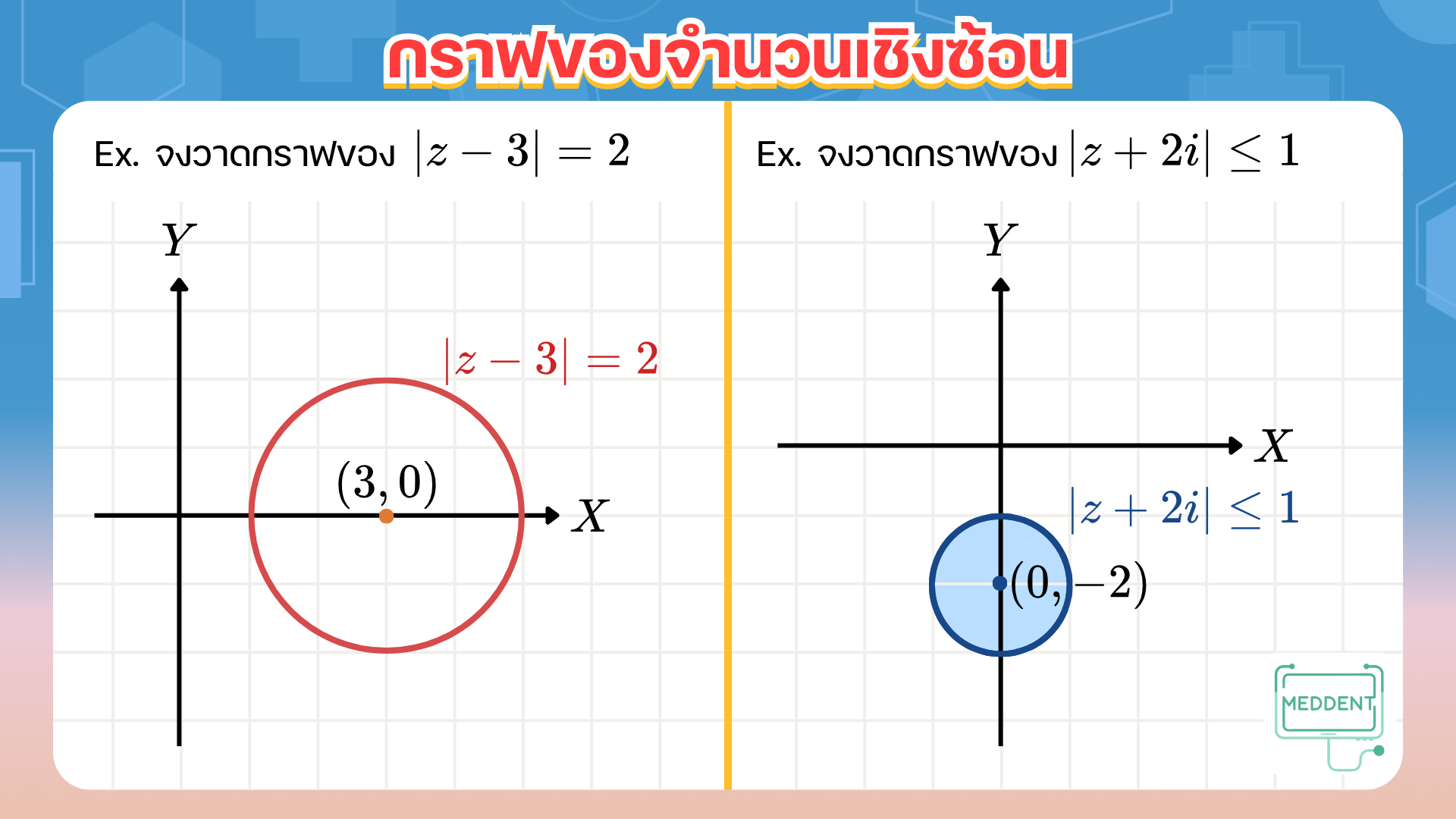
ถ้า z0=h+kiz_0 = h+ki เป็นจำนวนเชิงซ้อน และ rr เป็นจำนวนจริงบวก จะได้ว่า ∣z−z0∣=r\left| z - z_0 \right| = r จะเป็นวงกลมที่มีจุดศูนย์กลางอยู่ที่จุด (h,k)(h,k) รัศมี rr หน่วย ซึ่งจะเป็นจุดทั้งหมดที่มีระยะห่างจาก z0z_0 เท่ากับ rr หน่วย

Post

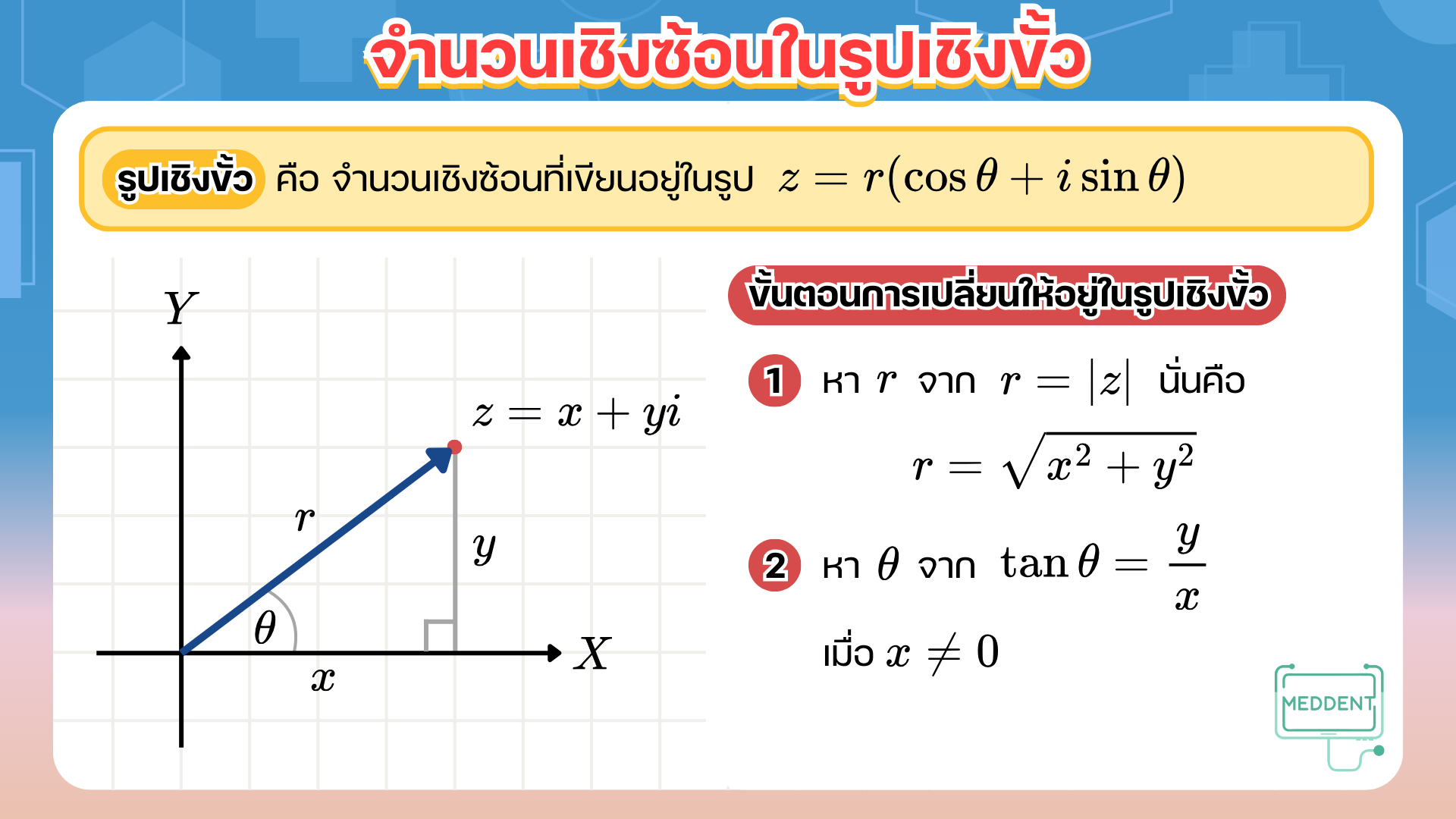
จำนวนเชิงซ้อนในรูปเชิงขั้ว

การแปลงจำนวนเชิงซ้อนในรูปแบบปกติให้อยู่ในรูปเชิงขั้ว

Post

ในเรื่องนี้ได้ใช้เรื่องฟังก์ชันตรีโกณมิติ น้องๆ สามารถทบทวนความรู้เรื่องฟังก์ชันตรีโกณมิติ ซึ่งกดได้ที่นี่เลยค้าบบ

Ex. จงเขียนให้อยู่ในรูปเชิงขั้วของจำนวนเชิงซ้อน 1+3i1+\sqrt{3}i
วิธีทำ
เนื่องจาก 1+3i1+\sqrt{3}i จะได้ว่า ∣1+3i∣=12+(3)2=1+3=4=2\left|1+\sqrt{3}i\right| = \sqrt{1^2+(\sqrt{3})^2}=\sqrt{1+3} =\sqrt{4} = 2
และได้ว่า tan⁡θ=31=3\tan\theta = \displaystyle\frac{\sqrt{3}}{1} = \sqrt{3} และจำนวนเชิงซ้อน 1+3i1+\sqrt{3}i อยู่ในคอวดรันต์ที่ 1
ทำให้ได้ว่า θ=60∘\theta = 60^\circ หรือ θ=π3\theta = \displaystyle\frac{\pi}{3}
ดังนั้น รูปเชิงขั้วของจำนวนเชิงซ้อน 1+3i1+\sqrt{3}i คือ 2(cos⁡(π3)+isin⁡(π3))2 \left(\cos\left(\displaystyle\frac{\pi}{3}\right)+i\sin\left(\displaystyle\frac{\pi}{3}\right)\right)

Ex. จงเขียนให้อยู่ในรูปเชิงขั้วของจำนวนเชิงซ้อน −4+4i-4+4i
วิธีทำ
เนื่องจาก −4+4i-4+4i จะได้ว่า ∣−4+4i∣=(−4)2+42=16+16=32=42\left|-4+4i\right| = \sqrt{(-4)^2+4^2}=\sqrt{16+16} =\sqrt{32} = 4 \sqrt{2}
และได้ว่า tan⁡θ=4−4=−1\tan\theta = \displaystyle\frac{4}{-4} = -1 และจำนวนเชิงซ้อน −4+4i-4+4i อยู่ในคอวดรันต์ที่ 2
ทำให้ได้ว่า θ=135∘\theta = 135^\circ หรือ θ=3π4\theta = \displaystyle\frac{3\pi}{4}
ดังนั้น รูปเชิงขั้วของจำนวนเชิงซ้อน −4+4i-4+4i คือ 42(cos⁡(3π4)+isin⁡(3π4))4 \sqrt{2}\left(\cos\left(\displaystyle\frac{3\pi}{4}\right)+i\sin\left(\displaystyle\frac{3\pi}{4}\right)\right)

การแปลงจำนวนเชิงซ้อนในรูปเชิงขั้วให้อยู่ในรูปแบบปกติ
Ex. จงเขียนจำนวนเชิงซ้อนที่อยู่ในรูปเชิงขั้วต่อไปนี้ให้อยู่ในรูป a+bia+bi เมื่อ aa และ bb เป็นจำนวนจริง
(1) z1=4(cos⁡(π4)+isin⁡(π4))z_1 = 4 \left( \cos\left(\displaystyle\frac{\pi}{4}\right) + i \sin\left(\displaystyle\frac{\pi}{4}\right) \right)
วิธีทำ เนื่องจาก cos⁡(π4)=22\cos\left(\displaystyle\frac{\pi}{4}\right) = \displaystyle\frac{\sqrt{2}}{2} และ sin⁡(π4)=22\sin\left(\displaystyle\frac{\pi}{4}\right) = \displaystyle\frac{\sqrt{2}}{2} จะได้ว่า

z1=4(22+22i)=422+422i=22+22i \begin{align*} z_1 &= 4 \left( \displaystyle\frac{\sqrt{2}}{2} + \displaystyle\frac{\sqrt{2}}{2}i \right) \\ &= \displaystyle\frac{4\sqrt{2}}{2} + \displaystyle\frac{4\sqrt{2}}{2}i \\ &= 2\sqrt{2} + 2\sqrt{2}i \end{align*}

(2) z2=10(cos⁡(π3)+isin⁡(π3))z_2=10 \left( \displaystyle\cos\left(\frac{\pi}{3}\right) + i \displaystyle\sin\left(\frac{\pi}{3}\right) \right)
วิธีทำ เนื่องจาก cos⁡(π3)=12\cos\left(\displaystyle\frac{\pi}{3}\right) = \displaystyle\frac{1}{2} และ sin⁡(π3)=32\sin\left(\displaystyle\frac{\pi}{3}\right) = \displaystyle\frac{\sqrt{3}}{2} จะได้ว่า

z2=10(12+32i)=102+1032i=5+53i \begin{align*} z_2 &= 10 \left( \displaystyle\frac{1}{2} + \displaystyle\frac{\sqrt{3}}{2} i \right) \\ &= \displaystyle\frac{10}{2} + \displaystyle\frac{10\sqrt{3}}{2}i \\ &= 5 + 5\sqrt{3}i \end{align*}

(3) z3=3(cos⁡(π2)+isin⁡(π2))z_3 = 3 \left( \cos\left(\displaystyle\frac{\pi}{2}\right) + i \sin\left(\displaystyle\frac{\pi}{2}\right) \right)
วิธีทำ เนื่องจาก cos⁡(π2)=0\cos\left(\displaystyle\frac{\pi}{2}\right) = 0 และ sin⁡(π2)=1\sin\left(\displaystyle\frac{\pi}{2}\right) = 1 จะได้ว่า

z3=3(0+i(1))=3i \begin{align*} z_3 = 3 (0 + i(1)) = 3i \end{align*}

สมบัติของการดำเนินการของจำนวนเชิงซ้อนที่เขียนอยู่ในรูปเชิงขั้ว
ให้ z1=r1(cos⁡θ1+isin⁡θ1)z_1 = r_1(\cos\theta_1+i\sin\theta_1) และ z2=r2(cos⁡θ2+isin⁡θ2)z_2 = r_2(\cos\theta_2+i\sin\theta_2) โดยที่ z1≠0z_1 \neq 0 และ z2≠0z_2 \neq 0

  1. z1z2=r1r2(cos⁡(θ1+θ2)+isin⁡(θ1+θ2))z_1 z_2 = r_1 r_2 (\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2))
  2. 1z2=1r2(cos⁡(θ2)−isin⁡(θ2))\displaystyle\frac{1}{z_2} = \displaystyle\frac{1}{r_2} (\cos(\theta_2) - i \sin(\theta_2))
  3. z1z2=r1r2(cos⁡(θ1−θ2)+isin⁡(θ1−θ2))\displaystyle\frac{z_1}{z_2} = \displaystyle\frac{r_1}{r_2} (\cos(\theta_1 - \theta_2) + i \sin(\theta_1 - \theta_2))
  4. z1‾=r1(cos⁡(−θ1)+isin⁡(−θ1))\overline{z_1} = r_1 (\cos(-\theta_1) + i \sin(-\theta_1))

Ex. กำหนดให้ z1=6(cos⁡(π3)+isin⁡(π3))z_1 = 6 \left( \cos\left(\displaystyle\frac{\pi}{3}\right) + i \sin\left(\displaystyle\frac{\pi}{3}\right) \right) และ z2=2(cos⁡(π6)+isin⁡(π6))z_2 = 2 \left( \cos\left(\displaystyle\frac{\pi}{6}\right) + i \sin\left(\displaystyle\frac{\pi}{6}\right) \right)
จงหาค่าของ z1z2, z1z2z_1z_2,\ \displaystyle\frac{z_1}{z_2} และ z1‾\overline{z_1} ในรูปของ a+bia+bi เมื่อ aa และ bb เป็นจำนวนจริง

วิธีทำ ต่อไปจะหาค่าของ z1z2z_1z_2 จากสมบัติข้อที่ 1. ดังนี้

z1z2=r1r2(cos⁡(θ1+θ2)+isin⁡(θ1+θ2))=(6)(2)(cos⁡(π3+π6)+isin⁡(π3+π6))=12(cos⁡(2π6+π6)+isin⁡(2π6+π6))=12(cos⁡(3π6)+isin⁡(3π6))=12(cos⁡(π2)+isin⁡(π2))=12(0+i(1))=12i \begin{align*} z_1 z_2 &= r_1 r_2 (\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)) \\ &= (6)(2) \left( \cos\left(\displaystyle\frac{\pi}{3} + \displaystyle\frac{\pi}{6}\right) + i \sin\left(\displaystyle\frac{\pi}{3} + \displaystyle\frac{\pi}{6}\right) \right) \\ &= 12 \left( \cos\left(\displaystyle\frac{2\pi}{6} + \displaystyle\frac{\pi}{6}\right) + i \sin\left(\displaystyle\frac{2\pi}{6} + \displaystyle\frac{\pi}{6}\right) \right) \\ &= 12 \left( \cos\left(\displaystyle\frac{3\pi}{6}\right) + i \sin\left(\displaystyle\frac{3\pi}{6}\right) \right) \\ &= 12 \left( \cos\left(\displaystyle\frac{\pi}{2}\right) + i \sin\left(\displaystyle\frac{\pi}{2}\right) \right) \\ &= 12 \left( 0 + i(1) \right) \\ &= 12i \end{align*}

หาค่าของ z1z2\displaystyle\frac{z_1}{z_2} จากสมบัติข้อที่ 3. ดังนี้

z1z2=r1r2(cos⁡(θ1−θ2)+isin⁡(θ1−θ2))=62(cos⁡(π3−π6)+isin⁡(π3−π6))=3(cos⁡(π6)+isin⁡(π6))=3(32+12i)=332+32i \begin{align*} \displaystyle\frac{z_1}{z_2} &= \frac{r_1}{r_2} (\cos(\theta_1 - \theta_2) + i \sin(\theta_1 - \theta_2)) \\ &= \frac{6}{2} \left( \cos\left(\displaystyle\frac{\pi}{3} - \displaystyle\frac{\pi}{6}\right) + i \sin\left(\displaystyle\frac{\pi}{3} - \displaystyle\frac{\pi}{6}\right) \right) \\ &= 3 \left( \cos\left(\displaystyle\frac{\pi}{6}\right) + i \sin\left(\displaystyle\frac{\pi}{6}\right) \right) \\ &= 3 \left( \displaystyle\frac{\sqrt{3}}{2} + \displaystyle\frac{1}{2}i \right) \\ &= \displaystyle\frac{3\sqrt{3}}{2} + \displaystyle\frac{3}{2}i \end{align*}

หาค่าของ z1‾\overline{z_1} จากสมบัติข้อที่ 4. ดังนี้

z1‾=r1(cos⁡(−θ1)+isin⁡(−θ1))=6(cos⁡(−π3)+isin⁡(−π3))=6(12−32i)=3−33i \begin{align*} \overline{z_1} &= r_1 (\cos(-\theta_1) + i \sin(-\theta_1)) \\ &= 6 \left( \cos\left(-\displaystyle\frac{\pi}{3}\right) + i \sin\left(-\displaystyle\frac{\pi}{3}\right) \right) \\ &= 6 \left( \displaystyle\frac{1}{2} -\displaystyle\frac{\sqrt{3}}{2}i \right) \\ &= 3 - 3\sqrt{3}i \end{align*}

ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1
เรื่องจำนวนเชิงซ้อน (ปี 66)

ให้ AA แทนเซตของจำนวนเชิงซ้อน zz ทั้งหมดในระนาบเชิงซ้อน ซึ่งสอดคล้องกับอสมการ

∣z−i∣2+∣z+i∣2<4 \begin{align*} |z - i|^2 + \left|z + i\right|^2 < 4 \end{align*}

พิจารณาข้อความต่อไปนี้

ก) ถ้า w∈Aw \in A แล้ว Re⁡(w)∈A\operatorname{Re}(w) \in A
ข) ถ้า w∈Aw \in A แล้ว w‾∈A\overline{w} \in A
ค) ถ้า w∈Aw \in A แล้ว w2∈Aw^2 \in A

จากข้อความ ก) ข) และ ค) ข้างต้น ข้อใดถูกต้อง

  1. ข้อความ ก) ถูกต้องเพียงข้อเดียวเท่านั้น
  2. ข้อความ ข) ถูกต้องเพียงข้อเดียวเท่านั้น
  3. ข้อความ ก) และ ข) ถูกต้องเท่านั้น
  4. ข้อความ ข) และ ค) ถูกต้องเท่านั้น
  5. ข้อความ ก) ข) และ ค) ถูกต้อง

วิธีทำให้ z=x+yiz=x+yi เป็นจำนวนเชิงซ้อน จะได้ว่า

∣z−i∣2+∣z+i∣2<4∣(x+yi)−i∣2+∣(x+yi)+i∣2<4∣x+(y−1)i∣2+∣x+(y+1)i∣2<4(x2+(y−1)2)2+(x2+(y+1)2)2<4x2+(y−1)2+x2+(y+1)2<4x2+(y2−2y+1)+x2+(y2+2y+1)<42x2+2y2+2<4x2+y2+1<2x2+y2<1 \begin{align*} \left|z - i\right|^2 + \left|z + i\right|^2 &< 4 \\ \left|(x+yi) - i\right|^2 + \left|(x+yi) + i\right|^2 &< 4 \\ \left|x+(y-1)i\right|^2 + \left|x + (y+1)i\right|^2 &< 4 \\ \left(\sqrt{x^2+(y-1)^2} \right)^2 + \left(\sqrt{x^2+(y+1)^2} \right)^2 &< 4 \\ x^2+(y-1)^2 + x^2+(y+1)^2 &< 4 \\ x^2+(y^2-2y+1) + x^2 +(y^2+2y+1) &< 4 \\ 2x^2+2y^2+2 &< 4 \\ x^2+y^2+1 &< 2 \\ x^2+y^2 &< 1 \\ \end{align*}

เนื่องจาก z=x+yiz=x+yi จะได้ว่า ∣z∣=x2+y2\left|z\right| = \sqrt{x^2+y^2} ทำให้ได้ว่า ∣z∣<1\left|z\right| < 1
ดังนั้น AA เป็นเซตของจุดภายในทั้งหมดของวงกลมที่มีจุดศูนย์กลางอยู่ที่ (0,0)(0,0) รัศมียาว 1 หน่วยซึ่งไม่รวมจุดขอบ นั่นคือ A={z∈C | ∣z∣<1}A = \left\{ z \in \mathbb{C} \,\middle|\, |z| < 1 \right\} หรือ A={x+yi∈C | x2+y2<1}A = \left\{ x + yi \in \mathbb{C} \,\middle|\, x^2 + y^2 < 1 \right\}

ต่อไปจะพิจารณาข้อความแต่ละข้อดังนี้
ก) ถ้า w∈Aw \in A แล้ว Re⁡(w)∈A\operatorname{Re}(w) \in A
ให้ w=a+biw = a+bi เป็นจำนวนเชิงซ้อนในเซต AA จะได้ว่า −1<a<1-1 < a < 1
พิจารณา Re⁡(w)=a=a+0i\operatorname{Re}(w) = a = a + 0i ซึ่ง −1<a<1-1 < a < 1
ดังนั้น Re⁡(w)∈A\operatorname{Re}(w) \in A

ข) ถ้า w∈Aw \in A แล้ว w‾∈A\overline{w} \in A
ให้ w=a+biw = a+bi เป็นจำนวนเชิงซ้อนในเซต AA จะได้ว่า ∣w∣<1\left|w\right| < 1
เนื่องจาก ∣w‾∣=a2+(−b)2=a2+b2=∣w∣\left|\overline{w}\right| = \sqrt{a^2+(-b)^2} = \sqrt{a^2+b^2} = \left|w\right| นั่นคือ ∣w‾∣=∣w∣\left|\overline{w}\right| = \left|w\right|
ทำให้ได้ว่า ∣w‾∣<1\left|\overline{w}\right| < 1
ดังนั้น w‾∈A\overline{w} \in A

ค) ถ้า w∈Aw \in A แล้ว w2∈Aw^2 \in A
ให้ w=a+biw = a+bi เป็นจำนวนเชิงซ้อนในเซต AA จะได้ว่า ∣w∣<1\left|w\right| < 1
พิจารณา ∣w∣2=(a2+b2)2=a2+b2\left|w\right|^2 = \left(\sqrt{a^2+b^2}\right)^2 = a^2+b^2
และ w2=(a+bi)(a+bi)=a2+2abi+(bi)2=a2+2abi−b2=(a2−b2)+2abiw^2 = (a+bi)(a+bi) = a^2 +2abi + (bi)^2 = a^2 +2abi - b^2 = (a^2-b^2)+2abi
จะได้ว่า

∣w2∣=(a2−b2)2+(2ab)2=a4−2a2b2+b4+4a2b2=a4+2a2b2+b4=(a2+b2)2=a2+b2 \begin{align*} \left|w^2\right| &= \sqrt{(a^2-b^2)^2+(2ab)^2} \\ &=\sqrt{a^4 - 2a^2b^2+b^4 +4a^2b^2} \\ &=\sqrt{a^4 + 2a^2b^2+b^4} \\ &= \sqrt{(a^2+b^2)^2} \\ &= a^2+b^2 \end{align*}

จะเห็นว่า ∣w2∣=∣w∣\left|w^2\right| = \left|w\right|
ดังนั้น ∣w2∣<1\left|w^2\right| < 1
เพราะฉะนั้น w‾∈A\overline{w} \in A

ตอบ ข้อ 5. ข้อความ ก) ข) และ ค) ถูกต้อง