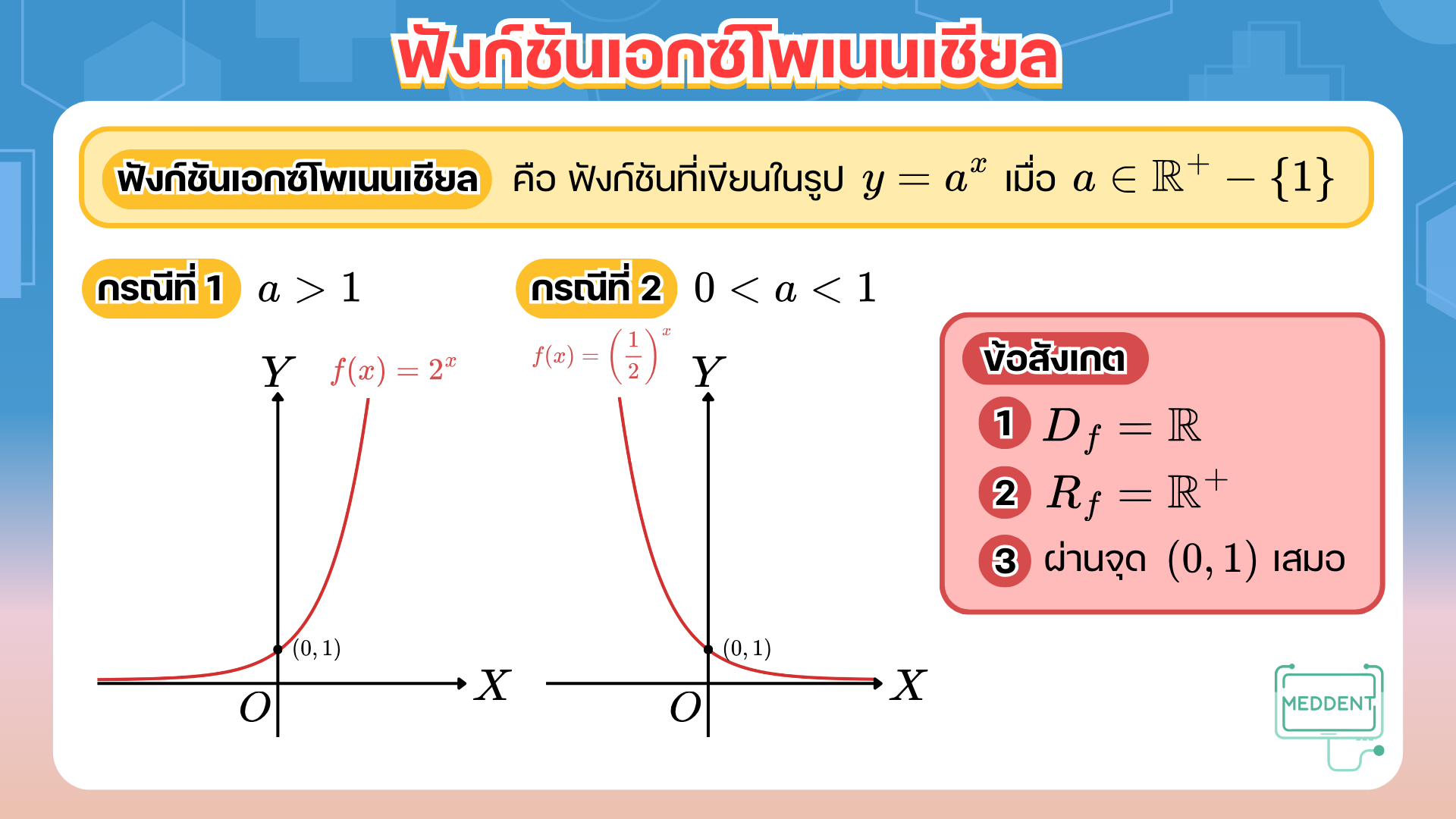
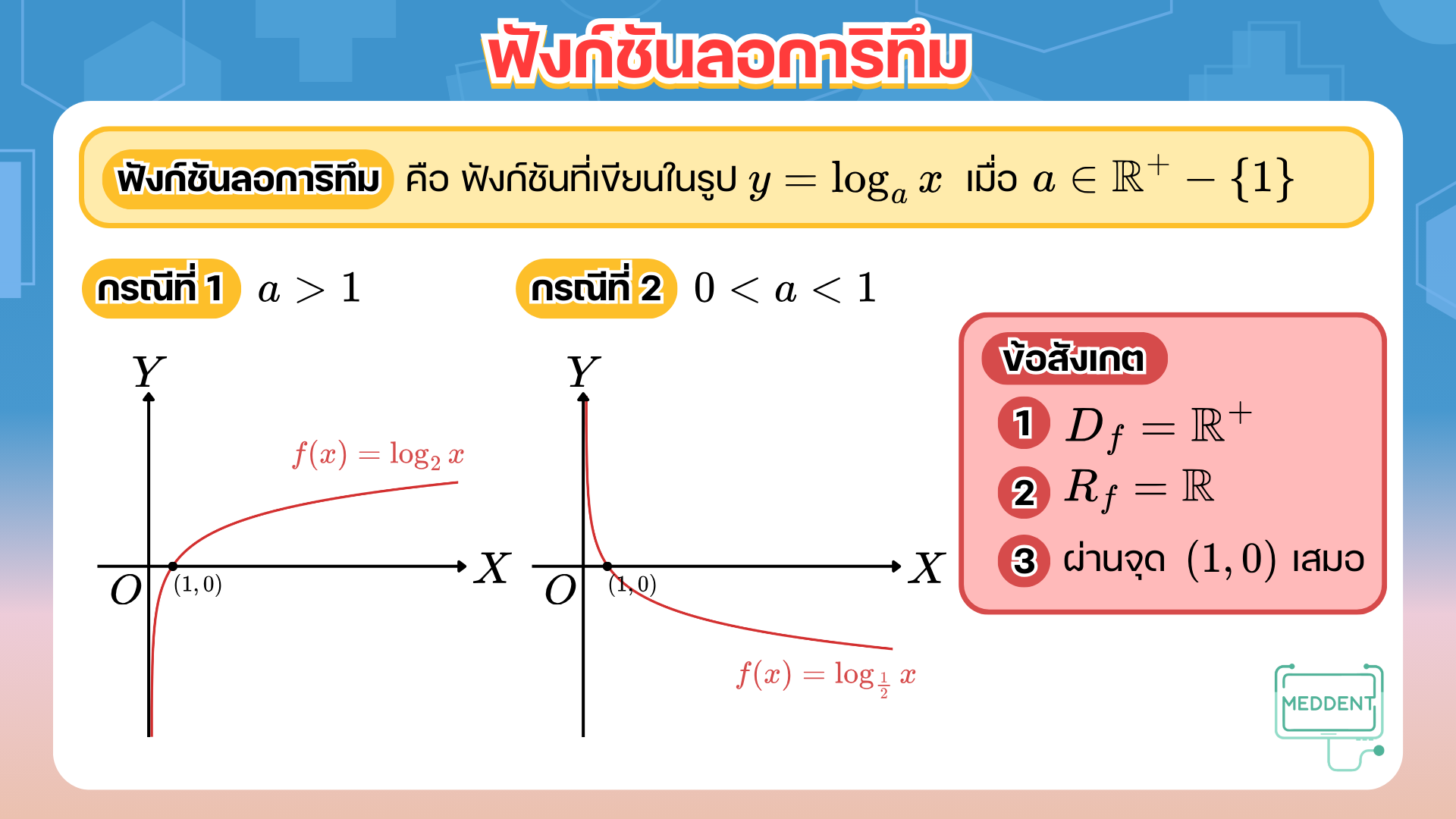
สวัสดีคร้าบบบ^^ วันนี้พี่หมอแม็คจะพาน้อง ๆ มาทำความรู้จักกับ ฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม บทนี้เป็นพื้นฐานสำคัญมากสำหรับการเรียนต่อทั้งเรื่องสมการ ฟังก์ชัน และการประยุกต์ต่าง ๆ ใน ม.ปลายเลยน้า~
ถ้าน้อง ๆ ยังงงว่าเอกซ์โพเนนเชียลคืออะไร ลอการิทึมใช้งานยังไง ไม่ต้องห่วงนะคั้บ! เพราะในโพสต์นี้พี่ได้ สรุปเนื้อหาแบบเข้าใจง่าย พร้อมตัวอย่างโจทย์ และมีเทคนิคเล็ก ๆ น้อย ๆ ในการทำข้อสอบมาฝากกันด้วย พร้อมแล้ว... ไปลุยกันเล้ยยย!
Ex.1 จงเขียนจำนวนต่อไปนี้ในรูปของเลขยกกำลังอย่างง่าย
243 = 3 × 3 × 3 × 3 × 3 = 3 5 243 = 3 \times 3 \times 3 \times 3 \times 3 = 3^5 243 = 3 × 3 × 3 × 3 × 3 = 3 5 64 3 = 2 × 2 × 2 × 2 × 2 × 2 3 = 2 × 2 = 2 2 \sqrt[3]{64} = \sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times 2} = 2 \times 2 = 2^2 3 64 = 3 2 × 2 × 2 × 2 × 2 × 2 = 2 × 2 = 2 2 12 − 4 = 1 12 4 = 1 2 8 ⋅ 3 4 12^{-4} = \displaystyle\frac{1}{12^4} = \displaystyle\frac{1}{2^8 \cdot 3^4} 1 2 − 4 = 1 2 4 1 = 2 8 ⋅ 3 4 1 7 0 = 1 7^0 = 1 7 0 = 1 Ex.2 จงเขียนจำนวนต่อไปนี้ในรูปอย่างง่าย
2 5 ⋅ 2 2 2 4 = 2 5 + 2 − 4 = 2 3 \displaystyle \frac{2^5 \cdot 2^2}{2^4} = 2^{5+2-4} = 2^3 2 4 2 5 ⋅ 2 2 = 2 5 + 2 − 4 = 2 3 ( 3 3 ⋅ 4 2 12 ) 2 = ( 3 3 ⋅ 4 2 3 ⋅ 4 ) 2 = ( 3 3 − 1 ⋅ 4 2 − 1 ) 2 = ( 3 2 ⋅ 4 1 ) 2 = ( 3 2 ⋅ 2 2 ) 2 = 3 4 ⋅ 2 4 \left(\frac{3^3 \cdot 4^2}{12}\right)^2 = \left(\displaystyle\frac{3^3 \cdot 4^2}{3 \cdot 4}\right)^2 = (3^{3-1} \cdot 4^{2-1})^2 = (3^{2} \cdot 4^{1})^2 = (3^{2} \cdot 2^{2})^2 = 3^{4} \cdot 2^{4} ( 12 3 3 ⋅ 4 2 ) 2 = ( 3 ⋅ 4 3 3 ⋅ 4 2 ) 2 = ( 3 3 − 1 ⋅ 4 2 − 1 ) 2 = ( 3 2 ⋅ 4 1 ) 2 = ( 3 2 ⋅ 2 2 ) 2 = 3 4 ⋅ 2 4 ( x 4 y 3 ) 2 x 5 y = x 8 y 6 x 5 y = x 8 − 5 y 6 − 1 = x 3 y 5 \displaystyle\frac{(x^4 y^3)^2}{x^5 y} = \frac{x^8 y^6}{x^5 y} = x^{8-5} y^{6-1} = x^3 y^5 x 5 y ( x 4 y 3 ) 2 = x 5 y x 8 y 6 = x 8 − 5 y 6 − 1 = x 3 y 5 ( 5 3 ⋅ 2 4 ) 2 10 6 ⋅ 2 = 5 6 ⋅ 2 8 5 6 ⋅ 2 7 = 5 6 − 6 ⋅ 2 8 − 7 = 5 0 ⋅ 2 1 = 2 \displaystyle\frac{(5^3 \cdot 2^4)^2}{10^6 \cdot 2} = \displaystyle\frac{5^6 \cdot 2^8}{5^6 \cdot 2^7} = 5^{6-6} \cdot 2^{8-7} = 5^0 \cdot 2^1 = 2 1 0 6 ⋅ 2 ( 5 3 ⋅ 2 4 ) 2 = 5 6 ⋅ 2 7 5 6 ⋅ 2 8 = 5 6 − 6 ⋅ 2 8 − 7 = 5 0 ⋅ 2 1 = 2 3 6 ⋅ 7 4 = 3 6 ⋅ 7 4 = 3 3 ⋅ 7 2 \sqrt{3^6 \cdot 7^4} = \sqrt{3^6} \cdot \sqrt{7^4} = 3^3 \cdot 7^2 3 6 ⋅ 7 4 = 3 6 ⋅ 7 4 = 3 3 ⋅ 7 2 x 6 y 4 z 3 x 3 z 2 3 = ( x 6 y 4 z 3 x 3 z 2 ) 1 3 = ( x 6 − 3 ⋅ y 4 ⋅ z 3 − 2 ) 1 3 = ( x 3 y 4 z ) 1 3 = x y 4 3 z 1 3 \sqrt[3]{\displaystyle\frac{x^6 y^4 z^3}{x^3 z^2}} = \left(\displaystyle\frac{x^6 y^4 z^3}{x^3 z^2}\right)^{\frac{1}{3}} = \left({x^{6-3} \cdot y^4 \cdot z^{3-2}}\right)^{\frac{1}{3}} = \left(x^3 y^4 z\right)^{\frac{1}{3}} = x y^{\frac{4}{3}} z^{\frac{1}{3}} 3 x 3 z 2 x 6 y 4 z 3 = ( x 3 z 2 x 6 y 4 z 3 ) 3 1 = ( x 6 − 3 ⋅ y 4 ⋅ z 3 − 2 ) 3 1 = ( x 3 y 4 z ) 3 1 = x y 3 4 z 3 1 Ex.3 จงหาคำตอบของสมการ x + x − 3 = 3 \sqrt{x+\sqrt{x-3}} = 3 x + x − 3 = 3 วิธีทำ เนื่องจาก x + x − 3 = 3 \sqrt{x+\sqrt{x-3}} = 3 x + x − 3 = 3
( x + x − 3 ) 2 = 3 2 x + x − 3 = 9 x − 3 = 9 − x \begin{align*} \left(\sqrt{x+\sqrt{x-3}}\right)^2\ &=\ 3^2 \\ x+\sqrt{x-3}\ &=\ 9 \\ \sqrt{x-3}\ &=\ 9-x \\ \end{align*} ( x + x − 3 ) 2 x + x − 3 x − 3 = 3 2 = 9 = 9 − x
( x − 3 ) 2 = ( 9 − x ) 2 x − 3 = 81 − 18 x + x 2 x 2 − 19 x + 84 = 0 ( x − 7 ) ( x − 12 ) = 0 x = 7 , 12 \begin{align*} \left(\sqrt{x-3}\right)^2\ &=\ (9-x)^2 \\ x-3\ &=\ 81 - 18x + x^2 \\ x^2 - 19x + 84\ &=\ 0 \\ (x-7)(x-12)\ &=\ 0 \\ x\ &=\ 7, 12 \end{align*} ( x − 3 ) 2 x − 3 x 2 − 19 x + 84 ( x − 7 ) ( x − 12 ) x = ( 9 − x ) 2 = 81 − 18 x + x 2 = 0 = 0 = 7 , 12
ตรวจคำตอบ ถ้า x = 7 x = 7 x = 7 7 + 7 − 3 = 7 + 4 = 7 + 2 = 9 = 3 \sqrt{7+\sqrt{7-3}} = \sqrt{7+\sqrt{4}} = \sqrt{7+2} = \sqrt{9} = 3 7 + 7 − 3 = 7 + 4 = 7 + 2 = 9 = 3 ถ้า x = 12 x = 12 x = 12 12 + 12 − 3 = 12 + 9 = 12 + 3 = 15 ≠ 3 \sqrt{12+\sqrt{12-3}} = \sqrt{12+\sqrt{9}} = \sqrt{12+3} = \sqrt{15} \neq 3 12 + 12 − 3 = 12 + 9 = 12 + 3 = 15 = 3
ดังนั้น คำตอบของสมการ x + x − 3 = 3 \sqrt{x+\sqrt{x-3}} = 3 x + x − 3 = 3 7 7 7
ในการแก้สมการที่มีราก น้อง ๆ ต้องระวังให้ดีนะครับ เพราะบางครั้งคำตอบที่เราหามาอาจไม่ใช่คำตอบของสมการก็ได้! อย่าลืม ตรวจคำตอบทุกครั้ง โดยการแทนค่ากลับเข้าไปในสมการเดิม เพื่อเช็คให้ชัวร์ว่าเป็นคำตอบที่ถูกต้องจริง ๆ นะคร้าบบ
Ex.4 จงหาคำตอบของสมการ ( 1 4 ) x 3 − x 2 + 2 = 16 x − ( x 3 + 1 ) \displaystyle \left( \frac{1}{4} \right)^{x^3 - x^2 + 2} = 16^{x - (x^3+1)} ( 4 1 ) x 3 − x 2 + 2 = 1 6 x − ( x 3 + 1 ) วิธีทำ
( 1 4 ) x 3 − x 2 + 2 = 16 x − ( x 3 + 1 ) ( 4 − 1 ) x 3 − x 2 + 2 = ( 4 2 ) x − ( x 3 + 1 ) 4 − x 3 + x 2 − 2 = 4 2 x − 2 x 3 − 2 \begin{align*} \left( \frac{1}{4} \right)^{x^3 - x^2 + 2}\ &=\ 16^{x - (x^3+1)} \\ (4^{-1})^{x^3 - x^2 + 2}\ &=\ (4^2)^{x - (x^3+1)} \\ 4^{-x^3 + x^2 - 2}\ &=\ 4^{2x - 2x^3 - 2} \end{align*} ( 4 1 ) x 3 − x 2 + 2 ( 4 − 1 ) x 3 − x 2 + 2 4 − x 3 + x 2 − 2 = 1 6 x − ( x 3 + 1 ) = ( 4 2 ) x − ( x 3 + 1 ) = 4 2 x − 2 x 3 − 2
เนื่องจาก f ( x ) = 4 x f(x) = 4^x f ( x ) = 4 x
− x 3 + x 2 − 2 = 2 x − 2 x 3 − 2 x 3 + x 2 − 2 x = 0 x ( x 2 + x − 2 ) = 0 x ( x − 1 ) ( x + 2 ) = 0 x = 0 , 1 , − 2 \begin{align*} -x^3 + x^2 - 2 \ &=\ 2x - 2x^3 - 2 \\ x^3 + x^2 - 2x\ &=\ 0 \\ x(x^2+x-2)\ &=\ 0 \\ x(x-1)(x+2)\ &=\ 0 \\ x\ &=\ 0, 1, -2 \end{align*} − x 3 + x 2 − 2 x 3 + x 2 − 2 x x ( x 2 + x − 2 ) x ( x − 1 ) ( x + 2 ) x = 2 x − 2 x 3 − 2 = 0 = 0 = 0 = 0 , 1 , − 2
ดังนั้น คำตอบของสมการ ( 1 4 ) x 3 − x 2 + 2 = 16 x − ( x 3 + 1 ) \displaystyle \left( \frac{1}{4} \right)^{x^3 - x^2 + 2} = 16^{x - (x^3+1)} ( 4 1 ) x 3 − x 2 + 2 = 1 6 x − ( x 3 + 1 ) 0 , 1 , − 2 0, 1, -2 0 , 1 , − 2
ฟังก์ชันลอการิทึมเป็นฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล เพราะค่าของฟังก์ชันลอการิทึมเป็นค่าที่ "ย้อนกลับ" จากฟังก์ชันเอกซ์โพเนนเชียลให้กลับมาเป็นค่าเดิมได้นั่นเองคั้บ!
สำหรับฟังก์ชันเอกซ์โพเนนเชียลเขียนอยู่รูป y = a x y = a^x y = a x x = log a y x = \log_a y x = log a y x x x y = a x y = a^x y = a x y y y y y y x = log a y x = \log_a y x = log a y x x x
Ex.5 กำหนดให้ a = 2 a = 2 a = 2
สำหรับฟังก์ชันเอกซ์โพเนนเชียล f ( x ) = 2 x f(x) = 2^x f ( x ) = 2 x ถ้า x = 4 x = 4 x = 4 y = f ( 4 ) = 2 4 = 16 y = f(4) = 2^4 = 16 y = f ( 4 ) = 2 4 = 16 สำหรับฟังก์ชันลอการิทึม g ( y ) = log 2 y g(y) = \log_2 y g ( y ) = log 2 y ถ้า y = 16 y = 16 y = 16 x = g ( 16 ) = log 2 16 = log 2 2 4 = 4 ⋅ log 2 2 = 4 ⋅ 1 = 4 x = g(16) = \log_2 16 = \log_2 2^4 = 4 \cdot \log_2 2 = 4 \cdot 1 = 4 x = g ( 16 ) = log 2 16 = log 2 2 4 = 4 ⋅ log 2 2 = 4 ⋅ 1 = 4 Ex.6 จงหาเซตคำตอบของสมการ log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) \log_3(x^2 - 4x + 3) = \log_3(x - 3) + \log_3(x - 1) log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) วิธีทำ เนื่องจาก log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) \log_3(x^2 - 4x + 3) = \log_3(x - 3) + \log_3(x - 1) log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) จะได้ว่า log 3 ( x 2 − 4 x + 3 ) = log 3 ( ( x − 3 ) ( x − 1 ) ) \log_3(x^2 - 4x + 3) = \log_3 \left((x - 3)(x - 1)\right) log 3 ( x 2 − 4 x + 3 ) = log 3 ( ( x − 3 ) ( x − 1 ) ) นั่นคือ log 3 ( x 2 − 4 x + 3 ) = log 3 ( x 2 − 4 x + 3 ) \log_3(x^2 - 4x + 3) = \log_3 \left(x^2 - 4x + 3\right) log 3 ( x 2 − 4 x + 3 ) = log 3 ( x 2 − 4 x + 3 )
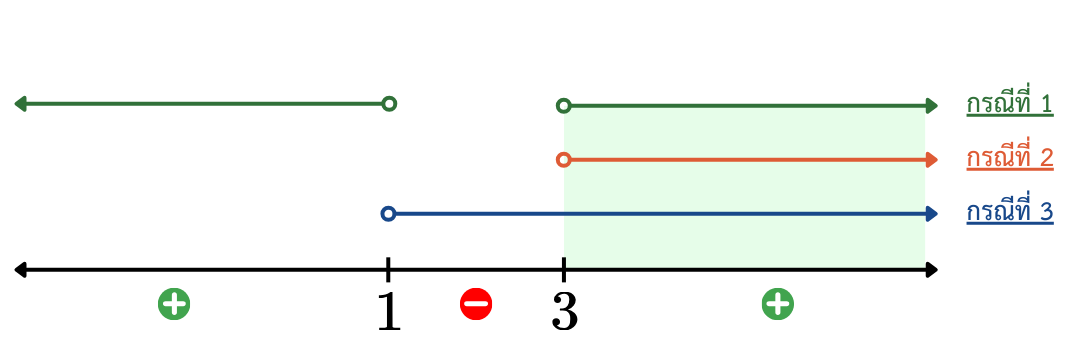
เนื่องจากฟังก์ชันลอการิทึม y = log 3 x y = \log_3 x y = log 3 x R + \mathbb{R}^+ R + x > 0 x>0 x > 0 กรณีที่ 1 x 2 − 4 x + 3 > 0 x^2 - 4x + 3 > 0 x 2 − 4 x + 3 > 0 ( x − 3 ) ( x − 1 ) > 0 (x - 3)(x - 1) > 0 ( x − 3 ) ( x − 1 ) > 0 กรณีที่ 2 x − 3 > 0 x - 3 > 0 x − 3 > 0 x > 3 x > 3 x > 3 กรณีที่ 3 x − 1 > 0 x - 1 > 0 x − 1 > 0 x > 1 x > 1 x > 1
ดังนั้น เซตคำตอบของสมการ log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) \log_3(x^2 - 4x + 3) = \log_3(x - 3) + \log_3(x - 1) log 3 ( x 2 − 4 x + 3 ) = log 3 ( x − 3 ) + log 3 ( x − 1 ) ( 3 , ∞ ) (3, \infty) ( 3 , ∞ )
กำหนดให้ p ( t ) p(t) p ( t ) 0 0 0 t t t
p ( t ) = 100 ( 1 − 2 − t 20 ) \begin{align*} p(t) = 100 \left(1-2^{-\frac{t}{20}}\right) \end{align*} p ( t ) = 100 ( 1 − 2 − 20 t )
ถ้าครั้งที่ 1 ธิดาชาร์จตัวเก็บประจุตัวนี้ที่มีปริมาณประจุไฟฟ้าเริ่มต้น 0 0 0 50 50 50 และครั้งที่ 2 ธิดาชาร์จตัวเก็บประจุตัวนี้ที่มีปริมาณประจุไฟฟ้าเริ่มต้น 0 0 0 87.5 87.5 87.5
วิธีทำ เนื่องจากธิดาชาร์จตัวเก็บประจุครั้งที่ 1 จนได้ปริมาณ 50 50 50 p ( t ) = 50 p(t) = 50 p ( t ) = 50
50 = 100 ( 1 − 2 − t 20 ) 1 − 2 − t 20 = 1 2 − 2 − t 20 = 1 2 − 1 − 2 − t 20 = − 1 2 2 − t 20 = 2 − 1 \begin{align*} 50\ &=\ 100 \left(1-2^{-\frac{t}{20}}\right) \\ 1-2^{-\frac{t}{20}}\ &=\ \displaystyle\frac{1}{2} \\ -2^{-\frac{t}{20}}\ &=\ \displaystyle\frac{1}{2} - 1 \\ -2^{-\frac{t}{20}}\ &=\ -\displaystyle\frac{1}{2} \\ 2^{-\frac{t}{20}}\ &=\ 2^{-1} \\ \end{align*} 50 1 − 2 − 20 t − 2 − 20 t − 2 − 20 t 2 − 20 t = 100 ( 1 − 2 − 20 t ) = 2 1 = 2 1 − 1 = − 2 1 = 2 − 1
เนื่องจากฟังก์ชันเอกซ์โพเนนเชียลเป็นฟังก์ชันหนึ่งต่อหนึ่ง จะได้ว่า
− t 20 = − 1 t = 20 \begin{align*} -\displaystyle\frac{t}{20}\ &=\ -1\\ t \ &=\ 20 \end{align*} − 20 t t = − 1 = 20
ดังนั้น ธิดาชาร์จตัวเก็บประจุครั้งที่ 1 เป็นระยะเวลา 20 20 20
เนื่องจากธิดาชาร์จตัวเก็บประจุครั้งที่ 2 จนได้ปริมาณ 87.5 87.5 87.5 p ( t ) = 87.5 p(t) = 87.5 p ( t ) = 87.5
87.5 = 100 ( 1 − 2 − t 20 ) 1 − 2 − t 20 = 87.5 100 − 2 − t 20 = 875 1000 − 1 − 2 − t 20 = − 125 1000 − 2 − t 20 = − 5 3 10 3 − 2 − t 20 = − 1 2 3 2 − t 20 = 2 − 3 \begin{align*} 87.5\ &=\ 100 \left(1-2^{-\frac{t}{20}}\right) \\ 1-2^{-\frac{t}{20}}\ &=\ \displaystyle\frac{87.5}{100} \\ -2^{-\frac{t}{20}}\ &=\ \displaystyle\frac{875}{1000} - 1 \\ -2^{-\frac{t}{20}}\ &=\ -\displaystyle\frac{125}{1000} \\ -2^{-\frac{t}{20}}\ &=\ -\displaystyle\frac{5^3}{10^3} \\ -2^{-\frac{t}{20}}\ &=\ -\displaystyle\frac{1}{2^3} \\ 2^{-\frac{t}{20}}\ &=\ 2^{-3} \\ \end{align*} 87.5 1 − 2 − 20 t − 2 − 20 t − 2 − 20 t − 2 − 20 t − 2 − 20 t 2 − 20 t = 100 ( 1 − 2 − 20 t ) = 100 87.5 = 1000 875 − 1 = − 1000 125 = − 1 0 3 5 3 = − 2 3 1 = 2 − 3
เนื่องจากฟังก์ชันเอกซ์โพเนนเชียลเป็นฟังก์ชันหนึ่งต่อหนึ่ง จะได้ว่า
− t 20 = − 3 t = 20 ⋅ 3 = 60 \begin{align*} -\displaystyle\frac{t}{20}\ &=\ -3\\ t \ &=\ 20 \cdot 3 = 60 \end{align*} − 20 t t = − 3 = 20 ⋅ 3 = 60
ดังนั้น ธิดาชาร์จตัวเก็บประจุครั้งที่ 2 เป็นระยะเวลา 60 60 60
เพราะฉะนั้น ธิดาชาร์จตัวเก็บประจุครั้งที่ 2 มากกว่าครั้งที่ 1 เป็นระยะเวลา 60 − 20 = 40 60-20 = 40 60 − 20 = 40
ตอบ 40 40 40