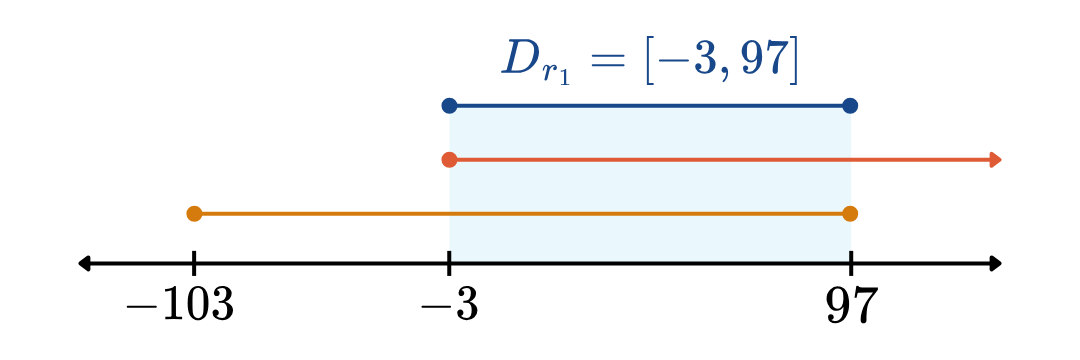สวัสดีคร้าบบบ^^ วันนี้พี่หมอแม็คจะพาน้อง ๆ มาเริ่มบท ความสัมพันธ์และฟังก์ชัน บทนี้ถือเป็นพื้นฐานสำคัญของ ม.ปลาย ที่ต้องใช้ต่อในหลายเรื่องเลยน้า~ ใครที่ยังงง ๆ ว่า ความสัมพันธ์คืออะไร ฟังก์ชันดูยังไง ไม่ต้องห่วงนะคับ! พี่สรุปเนื้อหาพร้อมตัวอย่างที่เข้าใจง่ายไว้ให้แล้ว แถมมีเทคนิคทำข้อสอบเล็ก ๆ มาฝากด้วยครับ ถ้าพร้อมแล้วไปลุยกันเล้ยยย!
คู่อันดับ (order pair) เป็นการจับคู่ของสิ่งของสองสิ่งที่มีความสัมพันธ์กัน เขียนแทนด้วย ( a , b ) (a, b) ( a , b ) การเท่ากันของคู่อันดับ ถ้าน้องมีคู่อันดับ 2 คู่ ให้น้องพิจารณาที่สมาชิกตัวหน้าและตัวหลังของคู่อันดับทั้งสองต้องมีค่าเท่ากันครับ ถึงจะสรุปได้ว่า คู่อันดับทั้งสองนั้นมีค่าเท่ากัน
Ex.1 จงหาว่าคู่อันดับ 2 คู่ที่กำหนดให้ในแต่ละข้อต่อไปนี้เท่ากันหรือไม่ เพราะเหตุใด
( 2 , − 3 ) (2, -3) ( 2 , − 3 ) ( 4 , 3 ) (4, 3) ( 4 , 3 ) ตอบ เนื่องจาก 2 ≠ 4 2 \neq 4 2 = 4 − 3 ≠ 3 -3 \neq 3 − 3 = 3 ดังนั้น ( 2 , − 3 ) ≠ ( 4 , 3 ) (2, -3) \neq (4, 3) ( 2 , − 3 ) = ( 4 , 3 ) ( 3 , 6 ) (3, 6) ( 3 , 6 ) ( 3 , 2 ⋅ 4 ) (3, 2 \cdot 4) ( 3 , 2 ⋅ 4 ) ตอบ เนื่องจาก 6 ≠ 2 ⋅ 4 = 8 6 \neq 2 \cdot 4 = 8 6 = 2 ⋅ 4 = 8 ดังนั้น ( 3 , 6 ) ≠ ( 3 , 2 ⋅ 4 ) (3, 6) \neq (3, 2 \cdot 4) ( 3 , 6 ) = ( 3 , 2 ⋅ 4 ) ( 4 , 16 ) (4, 16) ( 4 , 16 ) ( 2 2 , 4 2 ) (2^2, 4^2) ( 2 2 , 4 2 ) ตอบ เนื่องจาก 4 = 2 2 4 = 2^2 4 = 2 2 16 = 4 2 16 = 4^2 16 = 4 2 ดังนั้น ( 4 , 6 ) = ( 2 2 , 4 2 ) (4, 6) = (2^2, 4^2) ( 4 , 6 ) = ( 2 2 , 4 2 ) ผลคูณคาร์ทีเชียน ของ A A A B B B ( a , b ) (a, b) ( a , b ) a ∈ A a \in A a ∈ A b ∈ B b \in B b ∈ B A A A B B B A × B A \times B A × B
Ex.2 กำหนดให้ A = { 1 , 2 } A = \left\{1, 2\right\} A = { 1 , 2 } B = { a , b , c } B = \left\{a, b, c\right\} B = { a , b , c } A × B A \times B A × B B × A B \times A B × A
วิธีทำ
A × B = { ( 1 , a ) , ( 1 , b ) , ( 1 , c ) , ( 2 , a ) , ( 2 , b ) , ( 2 , c ) } A \times B = \left\{ (1, a),\ (1, b),\ (1, c),\ (2, a),\ (2, b),\ (2, c) \right\} A × B = { ( 1 , a ) , ( 1 , b ) , ( 1 , c ) , ( 2 , a ) , ( 2 , b ) , ( 2 , c ) } และ B × A = { ( a , 1 ) , ( a , 2 ) , ( b , 1 ) , ( b , 2 ) , ( c , 1 ) , ( c , 2 ) } B \times A = \left\{ (a, 1),\ (a, 2),\ (b, 1),\ (b, 2),\ (c, 1),\ (c, 2) \right\} B × A = { ( a , 1 ) , ( a , 2 ) , ( b , 1 ) , ( b , 2 ) , ( c , 1 ) , ( c , 2 ) }
น้อง ๆ จะเห็นว่า คู่อันดับทุกคู่ใน A × B A \times B A × B B × A B \times A B × A B × A B \times A B × A A × B A \times B A × B A × B ≠ B × A A \times B \neq B \times A A × B = B × A
เซต r r r ความสัมพันธ์ (relation) จาก A A A B B B r r r A × B A \times B A × B และเซต r r r A A A r r r A × A A \times A A × A
Ex.3 กำหนดให้ A = { 1 , 2 } A = \left\{1, 2\right\} A = { 1 , 2 } B = { a , b , c } B = \left\{a, b, c\right\} B = { a , b , c } ให้ r 1 = { ( 1 , a ) , ( 1 , b ) , ( 1 , c ) } r_1 = \left\{ (1, a),\ (1, b),\ (1, c) \right\} r 1 = { ( 1 , a ) , ( 1 , b ) , ( 1 , c ) } r 2 = { ( 1 , a ) , ( 2 , a ) , ( 3 , a ) } r_2 = \left\{ (1, a),\ (2, a),\ (3, a) \right\} r 2 = { ( 1 , a ) , ( 2 , a ) , ( 3 , a ) } จงหาว่า r 1 r_1 r 1 r 2 r_2 r 2 A A A B B B
วิธีทำ
เนื่องจาก r 1 ⊂ A × B r_1 \subset A \times B r 1 ⊂ A × B r 1 r_1 r 1 A A A B B B และจาก ( 3 , a ) ∉ A × B (3, a) \not\in A \times B ( 3 , a ) ∈ A × B r 2 ⊄ A × B r_2 \not\subset A \times B r 2 ⊂ A × B r 2 r_2 r 2 A A A B B B
กราฟ (graph) เป็นการแสดงให้เห็นลักษณะของความสัมพันธ์ของสิ่งของสองสิ่งให้เข้าใจได้ง่ายมากขึ้น โดยทั่วไปจะเป็นการแสดงบริเวณของ R × R \mathbb{R} \times \mathbb{R} R × R ระบบพิกัดฉาก (rectangular coordinate system) ซึ่งค่าบนแกน X X X Y Y Y
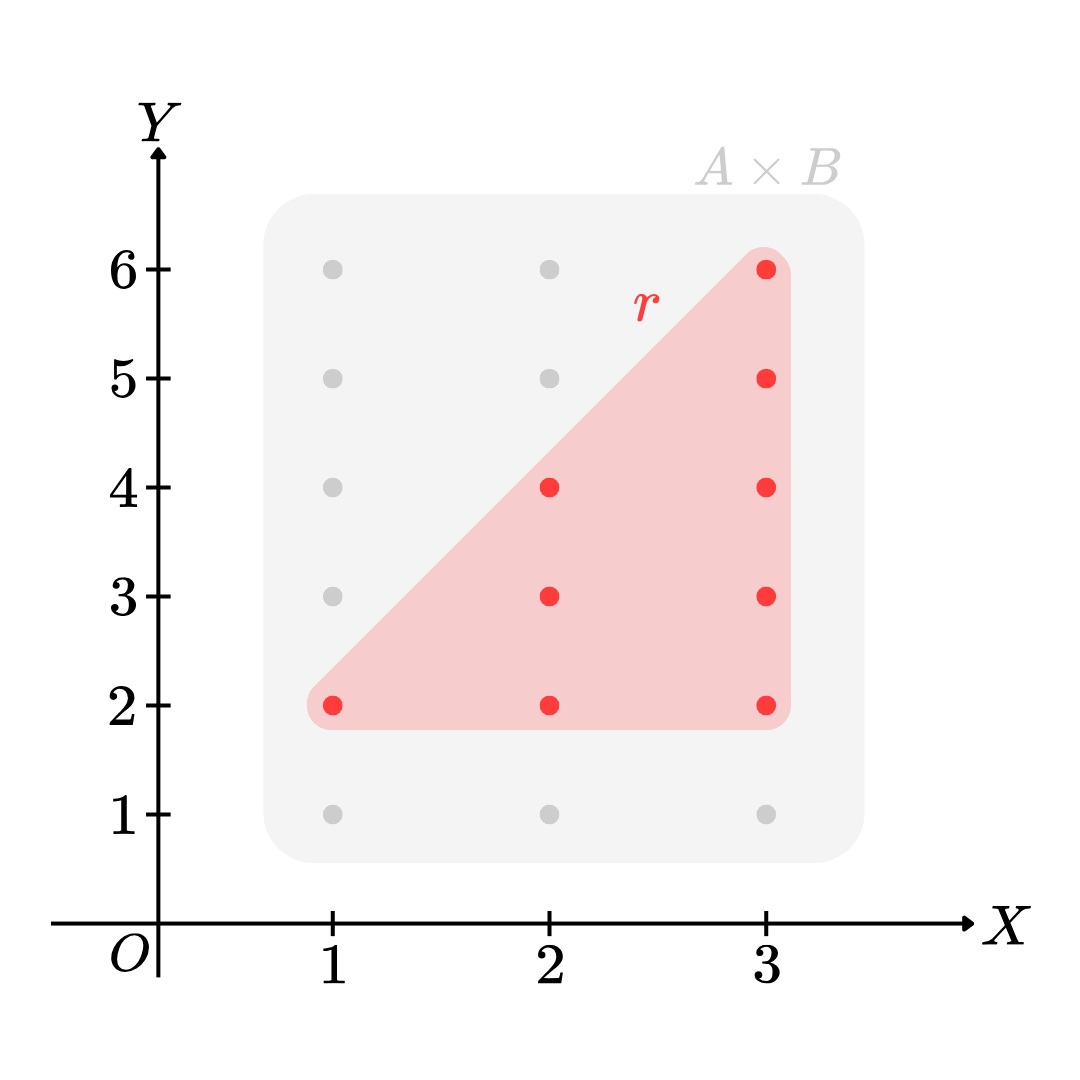
Ex.4 กำหนดให้ A = { 1 , 2 , 3 } A = \left\{1, 2, 3 \right\} A = { 1 , 2 , 3 } B = { 1 , 2 , 3 , 4 , 5 , 6 } B = \left\{1, 2, 3, 4, 5, 6\right\} B = { 1 , 2 , 3 , 4 , 5 , 6 } ถ้า r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) ( 3 , 6 ) } r = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5)\ (3, 6)\right\} r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) ( 3 , 6 ) } จงพิจารณาว่า r r r A A A B B B
วิธีทำ
เนื่องจาก r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } r = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5),\ (3, 6)\right\} r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } ซึ่งสมาชิกทุกตัวใน r r r A × B A \times B A × B r r r A A A B B B
Ex.5 กำหนดให้ A = { 1 , 2 , 3 } A = \left\{1, 2, 3 \right\} A = { 1 , 2 , 3 } r = { ( a , b ) ∣ a ∈ A และ b = a + 1 } r = \left\{ (a, b)\ |\ a \in A \text{ และ } b = a+1 \right\} r = { ( a , b ) ∣ a ∈ A และ b = a + 1 } จงพิจารณาว่า r r r A A A
วิธีทำ
เนื่องจาก r = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) } r = \left\{ (1, 2),\ (2, 3),\ (3, 4)\right\} r = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) } ( 3 , 4 ) ∉ A × A (3, 4) \not\in A \times A ( 3 , 4 ) ∈ A × A r ⊄ A × A r \not\subset A \times A r ⊂ A × A ดังนั้น r r r A A A
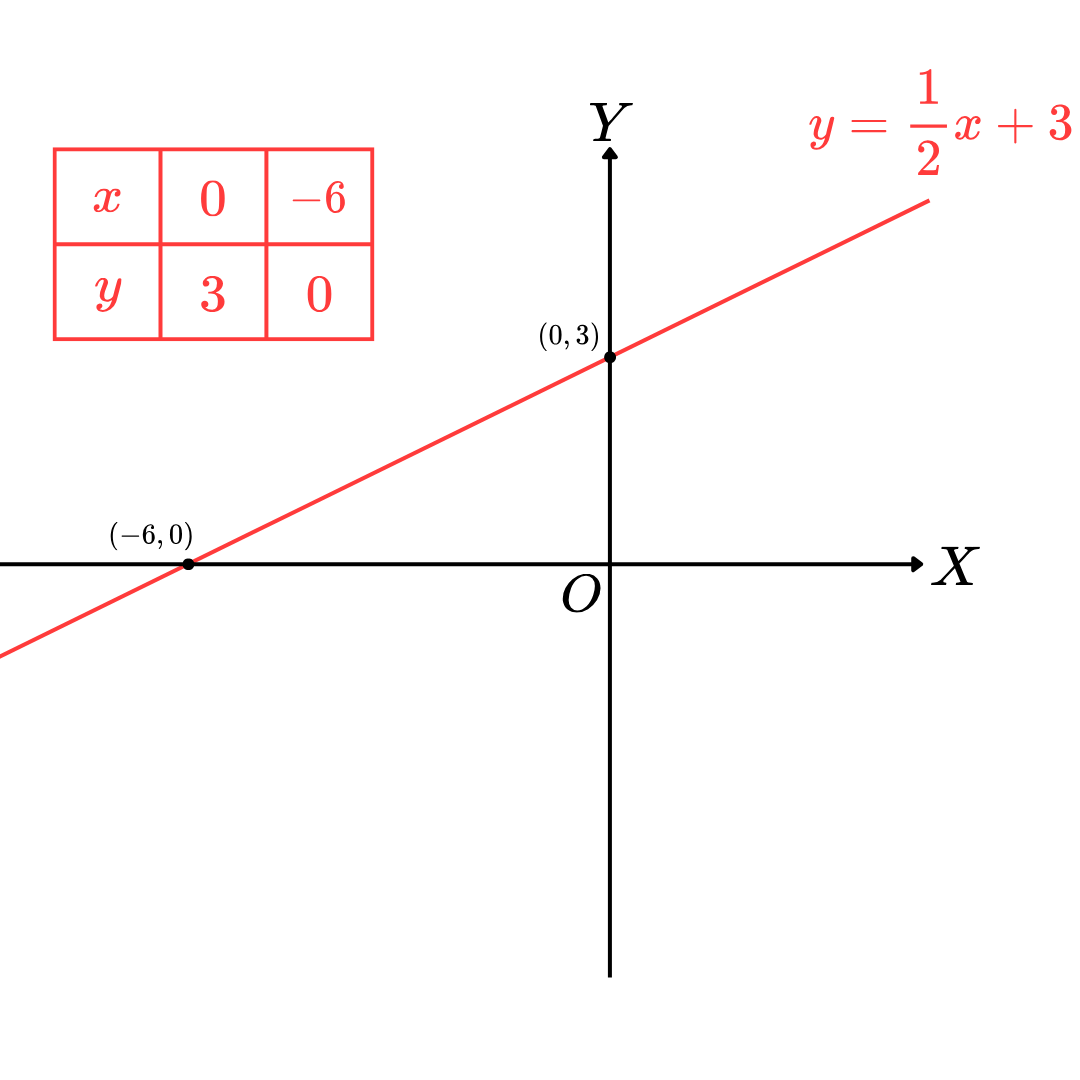
Ex.6 กำหนดให้ r = { ( x , y ) ∈ R × R | y = 1 2 x + 3 } r = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} r = { ( x , y ) ∈ R × R y = 2 1 x + 3 } จงวาดกราฟของความสัมพันธ์ r r r
วิธีทำ
เนื่องจาก y = x 2 + 3 \displaystyle y = \frac{x}{2}+3 y = 2 x + 3 r r r
โดเมน (Domain) ของ r r r D r D_r D r เรนจ์ (Range) ของ r r r R r R_r R r
Ex.7 จงหาโดเมนและเรนจ์ของความสัมพันธ์ต่อไปนี้
r 1 = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } r_1 = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5),\ (3, 6)\right\} r 1 = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } ตอบ D r = { 1 , 2 , 3 } D_r = \left\{ 1, 2, 3\right\} D r = { 1 , 2 , 3 } R r = { 2 , 3 , 4 , 5 , 6 } R_r = \left\{ 2, 3, 4, 5, 6 \right\} R r = { 2 , 3 , 4 , 5 , 6 } r 2 = { ( x , y ) ∈ R × R | y = 1 2 x + 3 } r_2 = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} r 2 = { ( x , y ) ∈ R × R y = 2 1 x + 3 } ตอบ D r = R D_r = \mathbb{R} D r = R R r = R R_r = \mathbb{R} R r = R r 3 = { ( x , y ) ∈ R × R | x 2 + y 2 = 4 } r_3 = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle x^2 + y^2 = 4 \right\} r 3 = { ( x , y ) ∈ R × R x 2 + y 2 = 4 } วิธีทำ (1) พิจารณาหาโดเมน D r D_r D r x x x เนื่องจาก x 2 + y 2 = 4 x^2 + y^2 = 4 x 2 + y 2 = 4 y 2 = 4 − x 2 y^2 = 4 - x^2 y 2 = 4 − x 2 y = ± 4 − x 2 y = \pm\sqrt{4 - x^2} y = ± 4 − x 2 พิจารณา 4 − x 2 ≥ 0 4 - x^2 \geq 0 4 − x 2 ≥ 0 x 2 − 4 ≤ 0 x^2 - 4 \leq 0 x 2 − 4 ≤ 0 ( x − 2 ) ( x + 2 ) ≤ 0 (x-2)(x+2) \leq 0 ( x − 2 ) ( x + 2 ) ≤ 0 x ∈ [ 0 , 2 ] x \in \left[0,2\right] x ∈ [ 0 , 2 ] เนื่องจาก y = ± 4 − x 2 y = \pm\sqrt{4 - x^2} y = ± 4 − x 2 x ∈ [ − 2 , 2 ] x \in \left[-2,2\right] x ∈ [ − 2 , 2 ] D r = [ − 2 , 2 ] D_r = \left[-2,2\right] D r = [ − 2 , 2 ] (2) พิจารณาหาเรนจ์ R r R_r R r y y y เนื่องจาก x 2 + y 2 = 4 x^2 + y^2 = 4 x 2 + y 2 = 4 x 2 = 4 − y 2 x^2 = 4 - y^2 x 2 = 4 − y 2 x = ± 4 − y 2 x = \pm\sqrt{4 - y^2} x = ± 4 − y 2 พิจารณา 4 − y 2 ≥ 0 4 - y^2 \geq 0 4 − y 2 ≥ 0 y 2 − 4 ≤ 0 y^2 - 4 \leq 0 y 2 − 4 ≤ 0 ( y − 2 ) ( y + 2 ) ≤ 0 (y-2)(y+2) \leq 0 ( y − 2 ) ( y + 2 ) ≤ 0 y ∈ [ 0 , 2 ] y \in \left[0,2\right] y ∈ [ 0 , 2 ] เนื่องจาก y = ± 4 − y 2 y = \pm\sqrt{4 - y^2} y = ± 4 − y 2 y ∈ [ − 2 , 2 ] y \in \left[-2,2\right] y ∈ [ − 2 , 2 ] R r = [ − 2 , 2 ] R_r = \left[-2,2\right] R r = [ − 2 , 2 ] ความสัมพันธ์ผกผัน ของ r r r r − 1 r^{-1} r − 1 TIPS D r − 1 = R r D_{r^{-1}} = R_r D r − 1 = R r R r − 1 = D r R_{r^{-1}} = D_r R r − 1 = D r
Ex.8 กำหนดให้ A = { 1 , 2 , 3 } A = \left\{1, 2, 3 \right\} A = { 1 , 2 , 3 } B = { 1 , 2 , 3 , 4 , 5 , 6 } B = \left\{1, 2, 3, 4, 5, 6\right\} B = { 1 , 2 , 3 , 4 , 5 , 6 } ถ้า r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } r = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5),\ (3, 6)\right\} r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } จงหา r − 1 , D r − 1 r^{-1}, D_{r^{-1}} r − 1 , D r − 1 R r − 1 R_{r^{-1}} R r − 1
วิธีทำ
จาก r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } r = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5),\ (3, 6)\right\} r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 ) } จะได้ว่า r − 1 = { ( 2 , 1 ) , ( 2 , 2 ) , ( 3 , 2 ) , ( 4 , 2 ) , ( 2 , 3 ) , ( 3 , 3 ) , ( 4 , 3 ) , ( 5 , 3 ) , ( 6 , 3 ) } r^{-1} = \left\{ (2, 1),\ (2, 2),\ (3, 2),\ (4, 2),\ (2, 3),\ (3, 3),\ (4, 3),\ (5, 3),\ (6, 3)\right\} r − 1 = { ( 2 , 1 ) , ( 2 , 2 ) , ( 3 , 2 ) , ( 4 , 2 ) , ( 2 , 3 ) , ( 3 , 3 ) , ( 4 , 3 ) , ( 5 , 3 ) , ( 6 , 3 ) } ทำให้ได้ว่า D r − 1 = { 2 , 3 , 4 , 5 , 6 } D_{r^{-1}} = \left\{ 2, 3, 4, 5, 6 \right\} D r − 1 = { 2 , 3 , 4 , 5 , 6 } R r − 1 = { 1 , 2 , 3 } R_{r^{-1}} = \left\{ 1, 2, 3\right\} R r − 1 = { 1 , 2 , 3 }
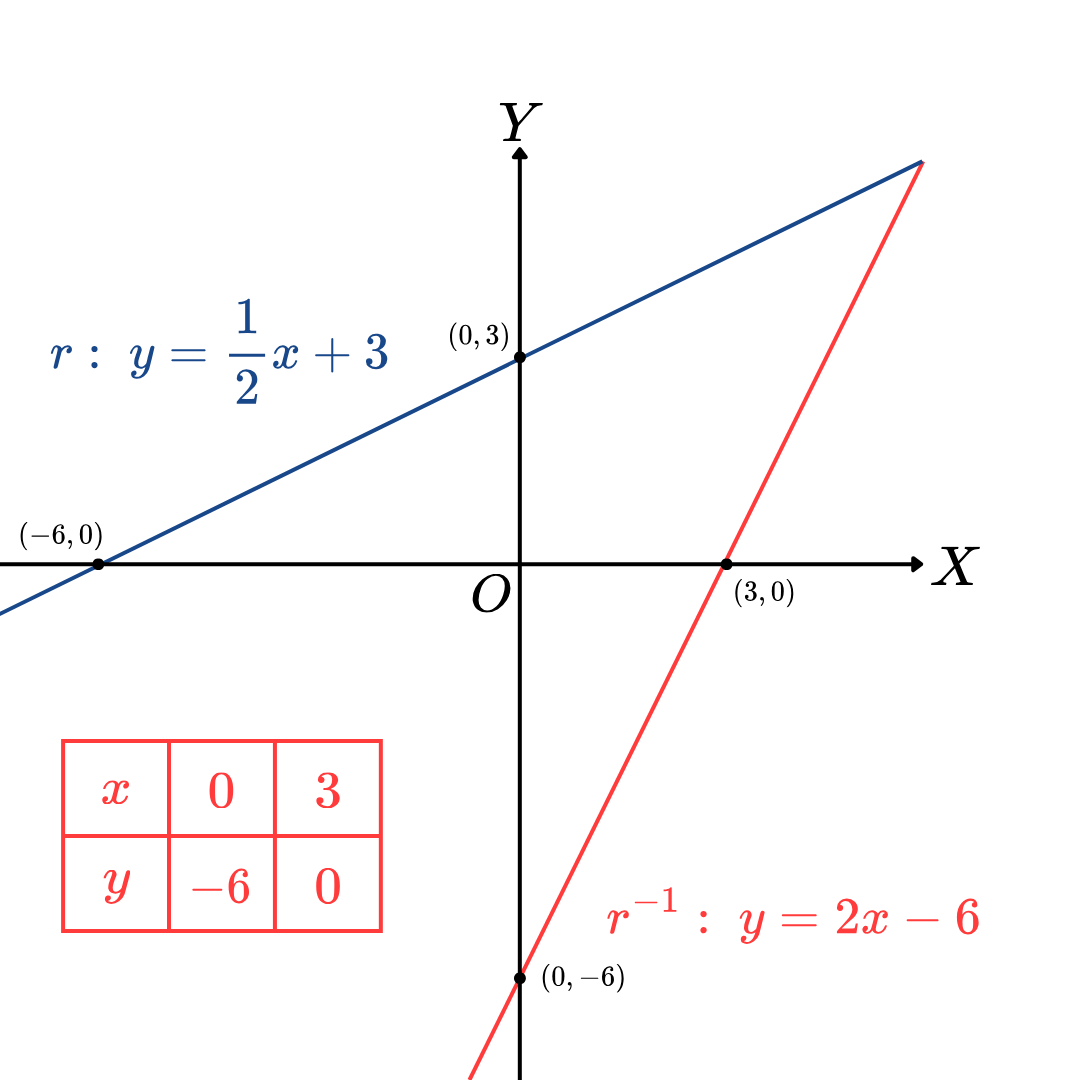
Ex.9 กำหนดให้ r = { ( x , y ) ∈ R × R | y = 1 2 x + 3 } r = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} r = { ( x , y ) ∈ R × R y = 2 1 x + 3 } จงหา r − 1 r^{-1} r − 1 r − 1 r^{-1} r − 1
วิธีทำ
จากความสัมพันธ์ r = { ( x , y ) ∈ R × R | y = 1 2 x + 3 } r = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} r = { ( x , y ) ∈ R × R y = 2 1 x + 3 }
r − 1 = { ( y , x ) ∈ R × R | y = 1 2 x + 3 } \begin{align*} r^{-1} = \left\{ (y, x)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} \end{align*} r − 1 = { ( y , x ) ∈ R × R y = 2 1 x + 3 }
หรือ
r − 1 = { ( x , y ) ∈ R × R | x = 1 2 y + 3 } = { ( x , y ) ∈ R × R | y = 2 x − 6 } \begin{align*} r^{-1} &= \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle x = \frac{1}{2}y+3 \right\} \\ &= \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = 2x - 6 \right\} \end{align*} r − 1 = { ( x , y ) ∈ R × R x = 2 1 y + 3 } = { ( x , y ) ∈ R × R ∣ y = 2 x − 6 }
ฟังก์ชัน (function) เป็นความสัมพันธ์ชนิดหนึ่งที่กำหนดให้สมาชิกตัวหน้าแต่ละตัวจับคู่กับสมาชิกตัวหลังเพียงตัวเดียวเท่านั้น
Ex.10 กำหนดให้ r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) ( 3 , 6 ) } r = \left\{ (1, 2),\ (2, 2), \ (2, 3),\ (2, 4),\ (3, 2), \ (3, 3),\ (3, 4),\ (3, 5)\ (3, 6)\right\} r = { ( 1 , 2 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) ( 3 , 6 ) } จงพิจารณาว่าความสัมพันธ์ r r r
วิธีทำ
เนื่องจาก ( 2 , 2 ) (2, 2) ( 2 , 2 ) ( 2 , 3 ) , (2, 3), ( 2 , 3 ) , r r r 1 1 1 ดังนั้น ความสัมพันธ์ r r r
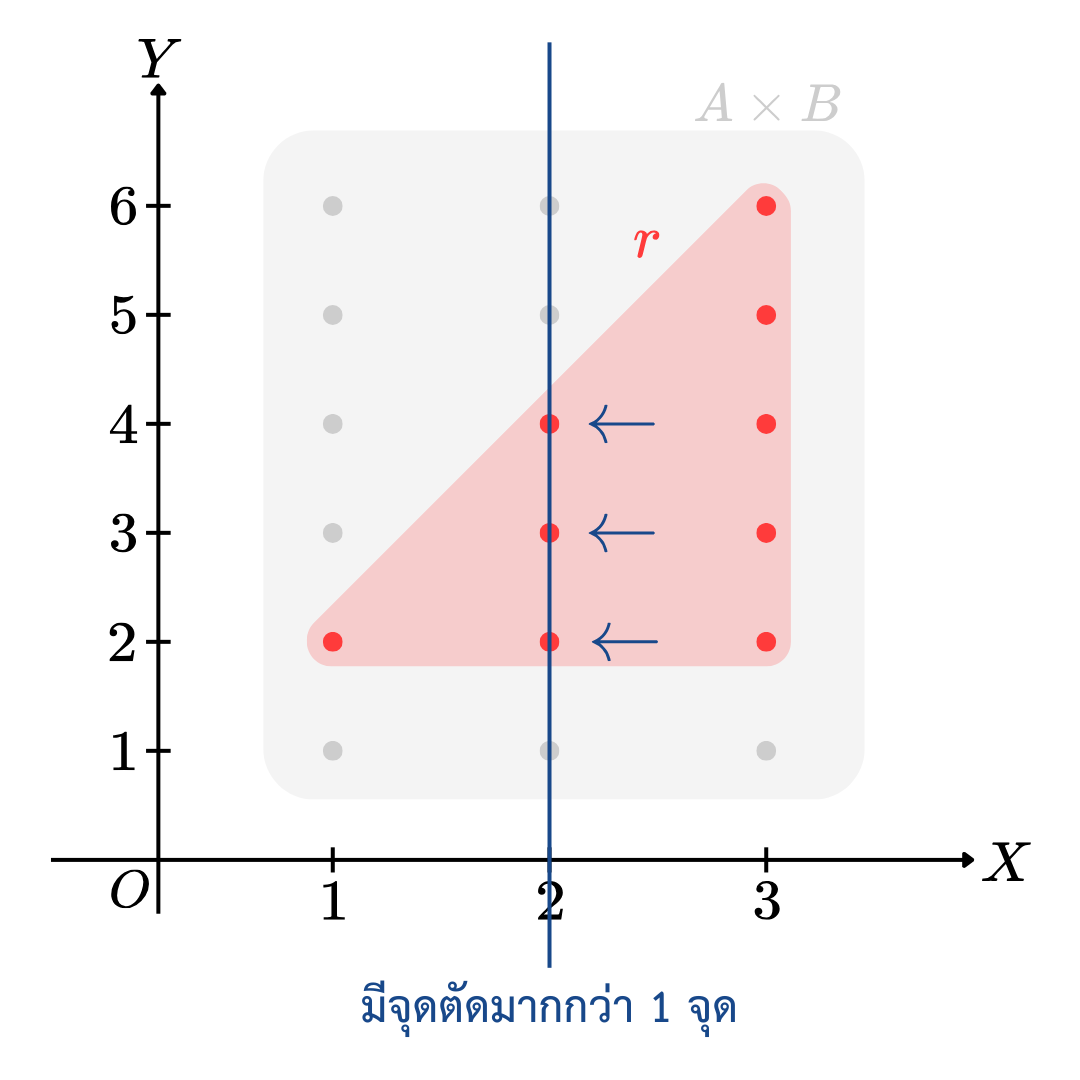
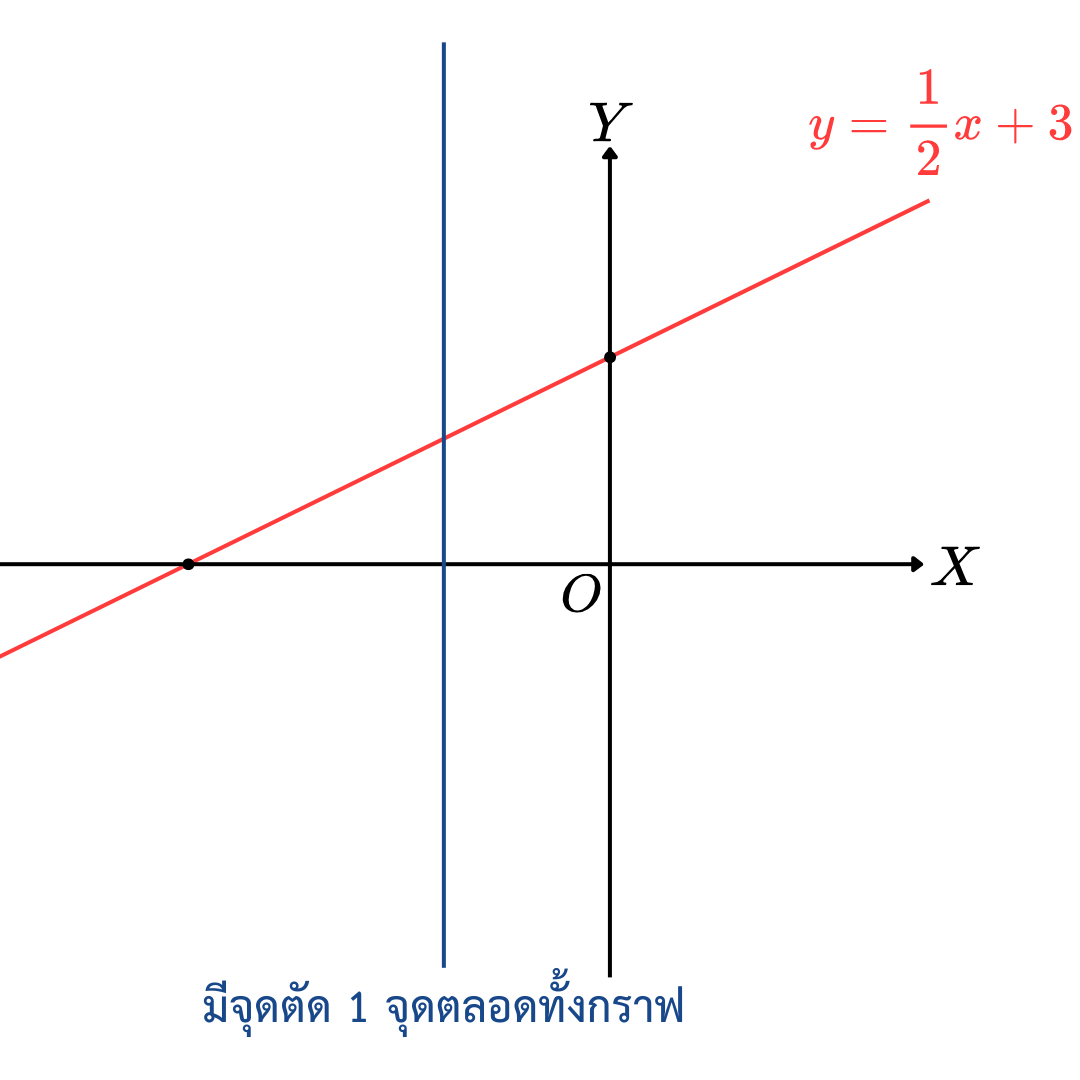
ในการตรวจสอบว่าความสัมพันธ์ใดเป็นฟังก์ชัน น้อง ๆ สามารถดูจากกราฟของความสัมพันธ์ได้ ถ้าเราลากเส้นตรงขนานกับแกน Y Y Y 1 1 1 r r r Y Y Y x = 2 x=2 x = 2 3 3 3 r r r
แต่ถ้ามีจุดตัดเพียงจุดเดียวตลอดทั้งกราฟ น้องๆ สามารถสรุปได้เลยครับว่า ความสัมพันธ์นั้นเป็นฟังก์ชัน
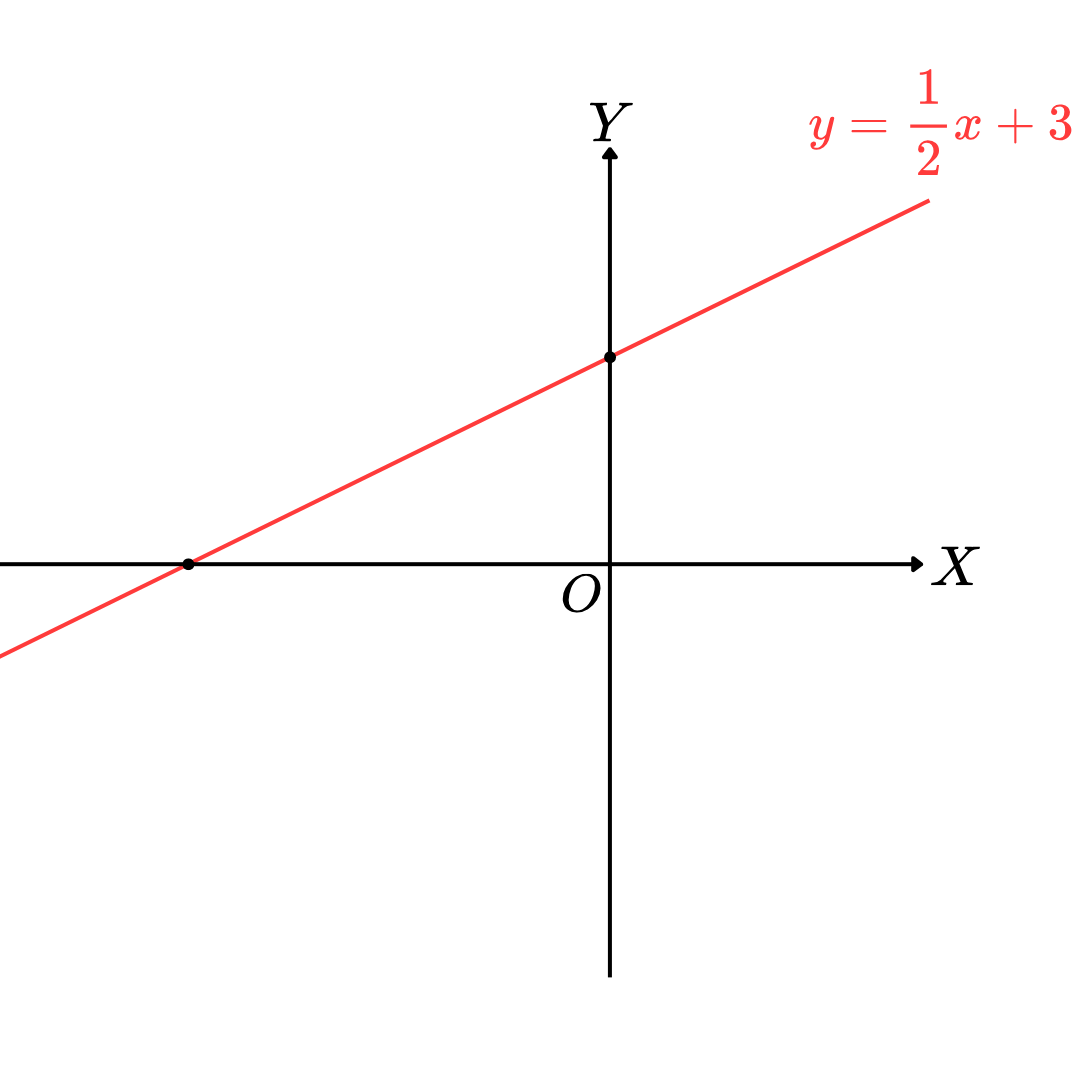
Ex.11 กำหนดให้ r = { ( x , y ) ∈ R × R | y = 1 2 x + 3 } r = \left\{ (x, y)\in \mathbb{R}\times\mathbb{R}\ \middle| \ \displaystyle y = \frac{1}{2}x+3 \right\} r = { ( x , y ) ∈ R × R y = 2 1 x + 3 } จงพิจารณาว่าความสัมพันธ์ r r r
วิธีทำ
พิจารณากราฟของความสัมพันธ์ r r r
เมื่อลากเส้นตรงขนานกับแกน Y Y Y r r r ดังนั้น ความสัมพันธ์ r r r
ให้ f f f g g g x x x การบวก f + g f+g f + g ( f + g ) ( x ) = f ( x ) + g ( x ) (f+g)(x) = f(x) + g(x) ( f + g ) ( x ) = f ( x ) + g ( x ) การลบ f − g f-g f − g ( f − g ) ( x ) = f ( x ) − g ( x ) (f-g)(x) = f(x) - g(x) ( f − g ) ( x ) = f ( x ) − g ( x ) การคูณ f g fg f g ( f g ) ( x ) = f ( x ) ⋅ g ( x ) (fg)(x) = f(x) \cdot g(x) ( f g ) ( x ) = f ( x ) ⋅ g ( x ) การหาร f g \displaystyle\frac{f}{g} g f ( f g ) ( x ) = f ( x ) g ( x ) \displaystyle\left(\frac{f}{g}\right)(x) = \displaystyle\frac{f(x)}{g(x)} ( g f ) ( x ) = g ( x ) f ( x ) g ( x ) ≠ 0 g(x) \neq 0 g ( x ) = 0
โดยที่โดเมน D f + g D_{f+g} D f + g D f − g D_{f-g} D f − g D f g D_{fg} D f g D f ∩ D g D_f \cap D_g D f ∩ D g และโดเมน D f g \displaystyle D_{\frac{f}{g}} D g f D f ∩ D g − { x ∈ D g | g ( x ) = 0 } D_f \cap D_g - \left\{ x \in D_g \middle| \ g(x) = 0 \right\} D f ∩ D g − { x ∈ D g ∣ g ( x ) = 0 }
Ex.12 กำหนดให้ f = { ( 1 , 2 ) , ( 2 , − 3 ) , ( 3 , 6 ) , ( 4 , 0 ) } f = \left\{ (1, 2),\ (2, -3), \ (3, 6), \ (4, 0) \right\} f = { ( 1 , 2 ) , ( 2 , − 3 ) , ( 3 , 6 ) , ( 4 , 0 ) } g = { ( 0 , − 2 ) , ( 1 , 4 ) , ( 2 , − 1 ) , ( 3 , 0 ) } g = \left\{ (0, -2),\ (1, 4), \ (2, -1), \ (3, 0) \right\} g = { ( 0 , − 2 ) , ( 1 , 4 ) , ( 2 , − 1 ) , ( 3 , 0 ) } จงหา f + g , f − g , f g f+g, f-g, fg f + g , f − g , f g f g \displaystyle\frac{f}{g} g f
วิธีทำ
พิจารณาหาการบวก f + g f+g f + g f − g f-g f − g f g fg f g f g \displaystyle\frac{f}{g} g f (1) f + g = { ( 1 , 6 ) , ( 2 , − 4 ) , ( 3 , 6 ) } f+g = \left\{ (1, 6),\ (2, -4), \ (3, 6) \right\} f + g = { ( 1 , 6 ) , ( 2 , − 4 ) , ( 3 , 6 ) } (2) f − g = { ( 1 , − 2 ) , ( 2 , − 2 ) , ( 3 , 6 ) } f-g = \left\{ (1, -2),\ (2, -2), \ (3, 6) \right\} f − g = { ( 1 , − 2 ) , ( 2 , − 2 ) , ( 3 , 6 ) } (3) f g = { ( 1 , 8 ) , ( 2 , 3 ) , ( 3 , 0 ) } fg = \left\{ (1, 8),\ (2, 3), \ (3, 0) \right\} f g = { ( 1 , 8 ) , ( 2 , 3 ) , ( 3 , 0 ) } (4) f g = { ( 1 , 1 2 ) , ( 2 , 3 ) } \displaystyle\frac{f}{g} = \left\{ \left(1, \displaystyle\frac{1}{2}\right),\ (2, 3) \right\} g f = { ( 1 , 2 1 ) , ( 2 , 3 ) } D f g = { 1 , 2 } \displaystyle D_{\frac{f}{g}} = \left\{ 1, 2 \right\} D g f = { 1 , 2 }
ต่อไปจะหาโดเมนของฟังก์ชันดังกล่าว พบว่าโดเมน D f + g D_{f+g} D f + g D f − g D_{f-g} D f − g D f g D_{fg} D f g D f ∩ D g = { 1 , 2 , 3 } D_f \cap D_g =\left\{ 1, 2, 3 \right\} D f ∩ D g = { 1 , 2 , 3 } และโดเมน D f g \displaystyle D_{\frac{f}{g}} D g f D f ∩ D g − { x ∈ D g | g ( x ) = 0 } = { 1 , 2 } D_f \cap D_g - \left\{ x \in D_g \middle| \ g(x) = 0 \right\} = \left\{ 1, 2 \right\} D f ∩ D g − { x ∈ D g ∣ g ( x ) = 0 } = { 1 , 2 }
Ex.13 กำหนดให้ f ( x ) = 1 x − 3 f(x) = \displaystyle\frac{1}{x-3} f ( x ) = x − 3 1 g ( x ) = x 2 − 1 g(x) = \sqrt{x^2-1} g ( x ) = x 2 − 1 จงหา f + g , f − g , f g f+g, f-g, fg f + g , f − g , f g f g \displaystyle\frac{f}{g} g f
วิธีทำ
พิจารณาหาการบวก f + g f+g f + g f − g f-g f − g f g fg f g f g \displaystyle\frac{f}{g} g f (1) ( f + g ) ( x ) = 1 x − 3 + x 2 − 1 (f+g)(x) = \displaystyle\frac{1}{x-3} + \sqrt{x^2-1} ( f + g ) ( x ) = x − 3 1 + x 2 − 1 (2) ( f − g ) ( x ) = 1 x − 3 − x 2 − 1 (f-g)(x) = \displaystyle\frac{1}{x-3} - \sqrt{x^2-1} ( f − g ) ( x ) = x − 3 1 − x 2 − 1 (3) ( f g ) ( x ) = x 2 − 1 x − 3 (fg)(x) = \displaystyle\frac{\sqrt{x^2-1}}{x-3} ( f g ) ( x ) = x − 3 x 2 − 1 (4) ( f g ) ( x ) = 1 x − 3 x 2 − 1 = 1 ( x − 3 ) x 2 − 1 \displaystyle\left(\frac{f}{g}\right)(x) = \displaystyle\frac{\displaystyle\frac{1}{x-3}}{\sqrt{x^2-1}} = \displaystyle\frac{1}{(x-3)\sqrt{x^2-1}} ( g f ) ( x ) = x 2 − 1 x − 3 1 = ( x − 3 ) x 2 − 1 1
ต่อไปจะหาโดเมนของฟังก์ชันดังกล่าว พบว่าพิจารณาหาโดเมน D f D_f D f x − 3 ≠ 0 x-3 \neq 0 x − 3 = 0 x ≠ 3 x \neq 3 x = 3 D f = R − { 3 } D_f = \mathbb{R} - \left\{ 3 \right\} D f = R − { 3 } และ D g D_g D g x 2 − 1 ≥ 0 x^2-1 \geq 0 x 2 − 1 ≥ 0 ( x − 1 ) ( x + 1 ) ≥ 0 (x-1)(x+1) \geq 0 ( x − 1 ) ( x + 1 ) ≥ 0 D g = ( − ∞ , − 1 ] ∪ [ 1 , ∞ ) D_g = (-\infty, -1] \cup [1, \infty) D g = ( − ∞ , − 1 ] ∪ [ 1 , ∞ ) เพราะฉะนั้น โดเมน D f + g D_{f+g} D f + g D f − g D_{f-g} D f − g D f g D_{fg} D f g D f ∩ D g = ( − ∞ , − 1 ] ∪ [ 1 , 3 ) ∪ ( 3 , ∞ ) D_f \cap D_g = (-\infty, -1] \cup [1, 3) \cup (3, \infty) D f ∩ D g = ( − ∞ , − 1 ] ∪ [ 1 , 3 ) ∪ ( 3 , ∞ )
เนื่องจาก x 2 − 1 = 0 \sqrt{x^2-1} = 0 x 2 − 1 = 0 x 2 − 1 = 0 x^2-1 = 0 x 2 − 1 = 0 ( x − 1 ) ( x + 1 ) = 0 (x-1)(x+1) = 0 ( x − 1 ) ( x + 1 ) = 0 ดังนั้น x = 1 , − 1 x = 1, -1 x = 1 , − 1 x x x g ( x ) = 0 g(x) = 0 g ( x ) = 0 1 1 1 − 1 -1 − 1 เพราะฉะนั้น โดเมน D f g \displaystyle D_{\frac{f}{g}} D g f D f ∩ D g − { x ∈ D g | g ( x ) = 0 } = ( − ∞ , − 1 ) ∪ ( 1 , 3 ) ∪ ( 3 , ∞ ) D_f \cap D_g - \left\{ x \in D_g \middle| \ g(x) = 0 \right\} = (-\infty, -1) \cup(1, 3) \cup (3, \infty) D f ∩ D g − { x ∈ D g ∣ g ( x ) = 0 } = ( − ∞ , − 1 ) ∪ ( 1 , 3 ) ∪ ( 3 , ∞ )
ฟังก์ชันประกอบ (composite function) เขียนแทนด้วย g ∘ f g \circ f g ∘ f ( g ∘ f ) ( x ) = g ( f ( x ) ) (g \circ f)(x) = g(f(x)) ( g ∘ f ) ( x ) = g ( f ( x )) โดยที่โดเมน D g ∘ f D_{g \circ f} D g ∘ f { x ∈ D f | f ( x ) ∈ D g } \left\{ x \in D_f \middle| \ f(x) \in D_g \right\} { x ∈ D f ∣ f ( x ) ∈ D g } TIPS ถ้า R f ∩ D g = ∅ R_f \cap D_g = \varnothing R f ∩ D g = ∅ g ∘ f g \circ f g ∘ f
Ex.14 กำหนดให้ f ( x ) = 1 − x 2 f(x) = \sqrt{1 - x^2} f ( x ) = 1 − x 2 g ( x ) = x 2 + 2 g(x) = x^2+2 g ( x ) = x 2 + 2 จงหา g ∘ f g \circ f g ∘ f f ∘ g f \circ g f ∘ g
วิธีทำ
(1) พิจารณาหาเรนจ์ R f R_f R f D g D_g D g ให้ y = 1 − x 2 y = \sqrt{1 - x^2} y = 1 − x 2 y 2 = 1 − x 2 y^2 = 1 - x^2 y 2 = 1 − x 2 y ≥ 0 y \geq 0 y ≥ 0 x 2 + y 2 = 1 x^2 + y^2 = 1 x 2 + y 2 = 1 ( 0 , 0 ) (0,0) ( 0 , 0 ) 1 1 1 R f = [ 0 , 1 ] R_f = [0, 1] R f = [ 0 , 1 ] และเนื่องจากสามารถหาค่า g ( x ) = x 2 + 2 g(x) = x^2+2 g ( x ) = x 2 + 2 x x x D g = R D_g = \mathbb{R} D g = R พบว่า R f ∩ D g = [ 0 , 1 ] ∩ R = [ 0 , 1 ] R_f \cap D_g = [0, 1] \cap \mathbb{R} = [0, 1] R f ∩ D g = [ 0 , 1 ] ∩ R = [ 0 , 1 ] ดังนั้น ( g ∘ f ) ( x ) = g ( f ( x ) ) = g ( 1 − x 2 ) = ( 1 − x 2 ) 2 + 2 = ∣ 1 − x 2 ∣ + 2 (g \circ f)(x) = g(f(x)) = g\left( \sqrt{1 - x^2} \right) = \left( \sqrt{1 - x^2} \right)^2+2 = \left| 1 - x^2 \right| +2 ( g ∘ f ) ( x ) = g ( f ( x )) = g ( 1 − x 2 ) = ( 1 − x 2 ) 2 + 2 = 1 − x 2 + 2
(2) พิจารณาหาเรนจ์ R g R_g R g D f D_f D f เนื่องจาก y = x 2 + 2 y = x^2+2 y = x 2 + 2 ( 0 , 2 ) (0,2) ( 0 , 2 ) R f = [ 2 , ∞ ) R_f = [2, \infty) R f = [ 2 , ∞ ) และโดเมน D f D_f D f 1 − x 2 ≥ 0 1 - x^2 \geq 0 1 − x 2 ≥ 0 x 2 − 1 ≤ 0 x^2 - 1 \leq 0 x 2 − 1 ≤ 0 ( x − 1 ) ( x + 1 ) ≤ 0 (x-1)(x+1) \leq 0 ( x − 1 ) ( x + 1 ) ≤ 0 D f = [ − 1 , 1 ] D_f = [-1, 1] D f = [ − 1 , 1 ] พบว่า R g ∩ D f = [ 2 , ∞ ) ∩ [ − 1 , 1 ] = ∅ R_g \cap D_f = [2, \infty) \cap [-1, 1] = \varnothing R g ∩ D f = [ 2 , ∞ ) ∩ [ − 1 , 1 ] = ∅ ดังนั้น f ∘ g f \circ g f ∘ g
ฟังก์ชันเพิ่ม (increasing function) คือ ฟังก์ชันเมื่อ x x x y y y ฟังก์ชันลด (decreasing function) คือ ฟังก์ชันเมื่อ x x x y y y
Ex.15 จงหาช่วงที่ทำให้ฟังก์ชัน f f f f f f
1. f ( x ) = 1 2 x + 3 f(x) = \displaystyle\frac{1}{2}x+3 f ( x ) = 2 1 x + 3
เห็นว่าเมื่อ x x x y y y x x x ดังนั้น f f f R \mathbb{R} R
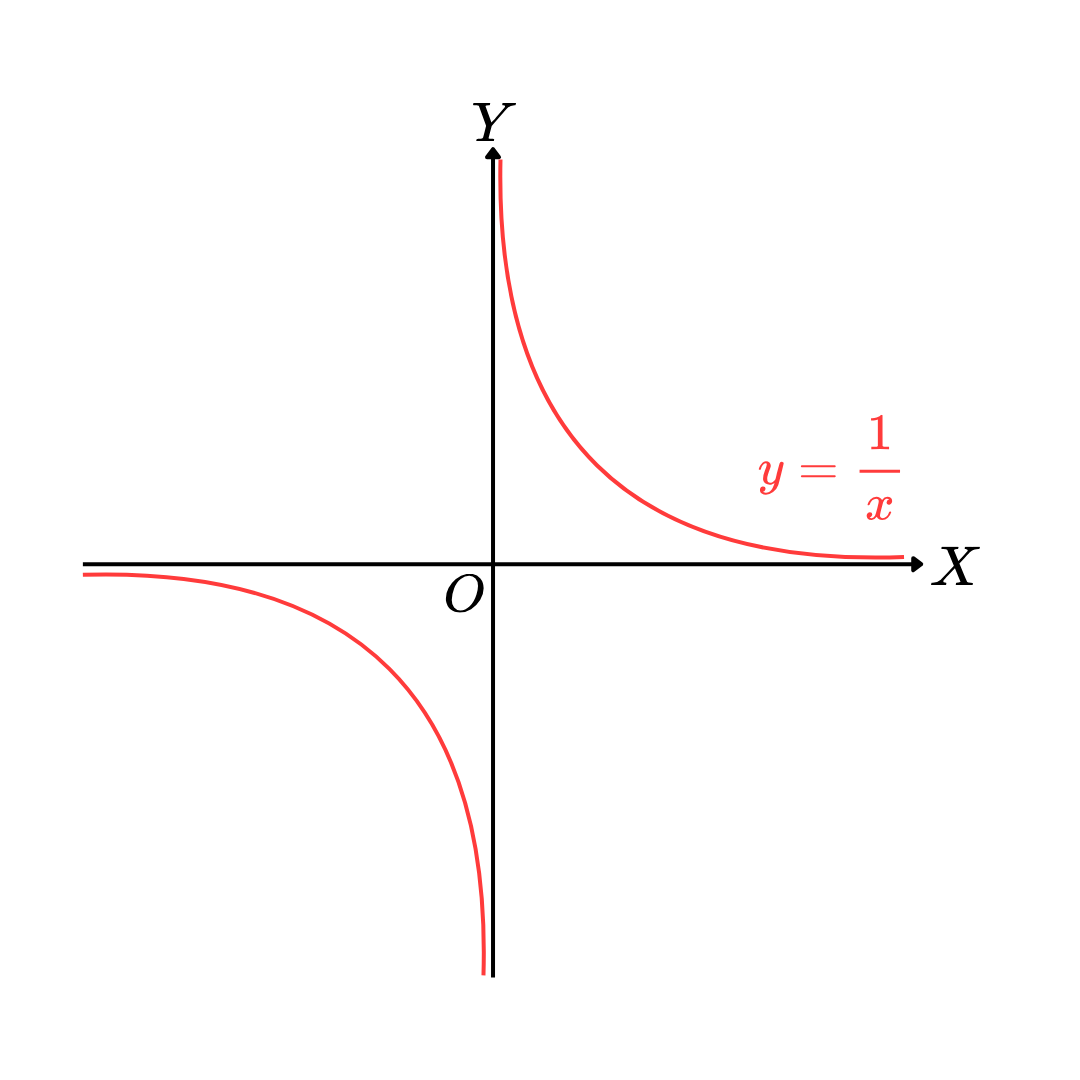
2. g ( x ) = 1 x g(x) = \displaystyle\frac{1}{x} g ( x ) = x 1
เห็นว่าเมื่อ x x x y y y x x x 0 0 0 ดังนั้น g g g R − { 0 } \mathbb{R} - \left\{ 0 \right\} R − { 0 }
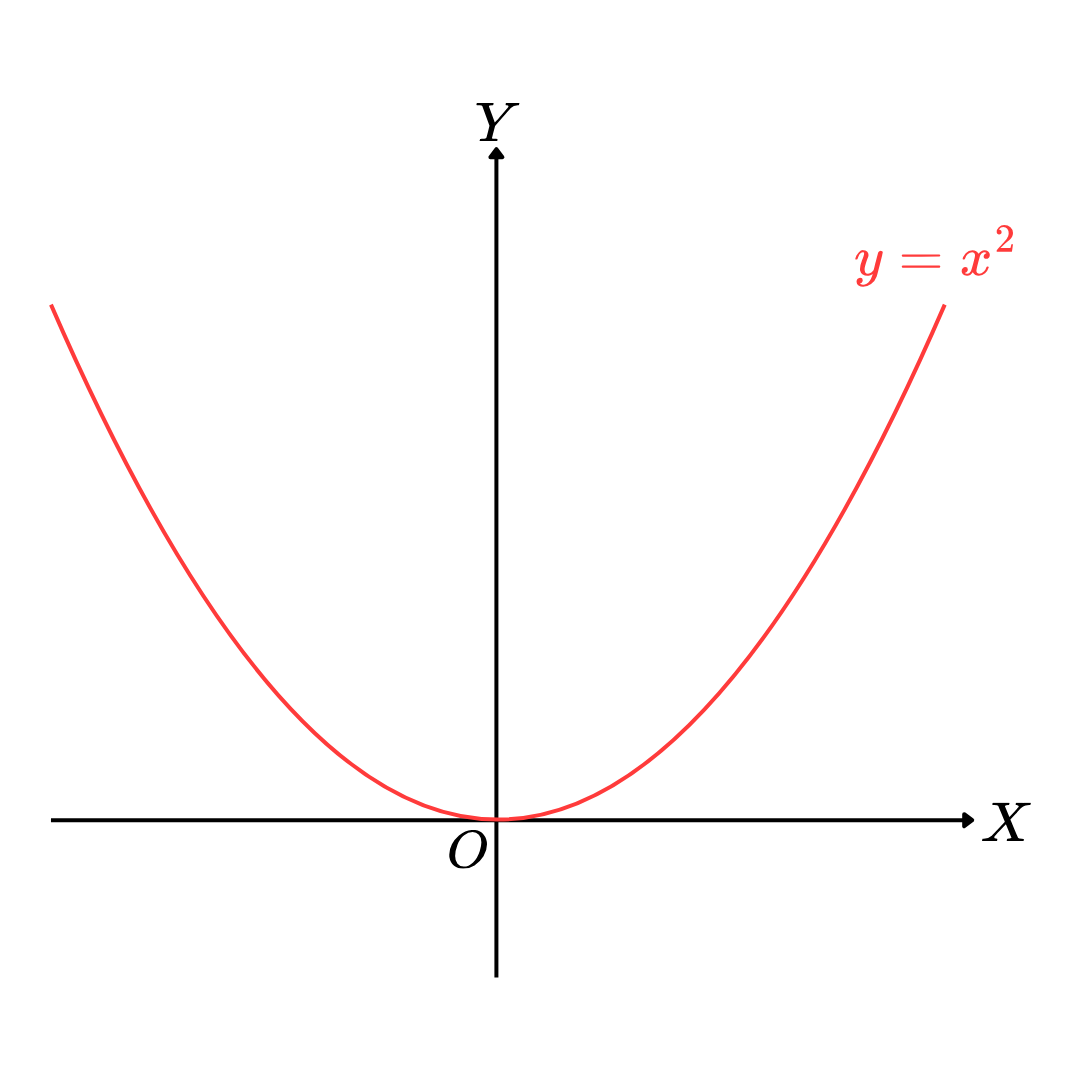
3. h ( x ) = x 2 h(x) = x^2 h ( x ) = x 2
เห็นว่าเมื่อ x x x y y y x x x 0 0 0 ดังนั้น h h h ( − ∞ , 0 ) (-\infty, 0) ( − ∞ , 0 ) เห็นว่าเมื่อ x x x y y y x x x 0 0 0 ดังนั้น h h h ( 0 , ∞ ) (0, \infty) ( 0 , ∞ )
ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1ถ้า r 1 = { ( x , y ) ∈ R × R | y = 10 − x + 3 } r_1 = \left\{(x,y) \in \mathbb{R} \times\mathbb{R} \middle| \ y= \sqrt{10 - \sqrt{x+3}} \right\} r 1 = { ( x , y ) ∈ R × R y = 10 − x + 3 } r 2 = { ( x , y ) ∈ R × R | y = 9 x 2 − 3 x − 4 } \displaystyle r_2 = \left\{(x,y) \in \mathbb{R} \times\mathbb{R} \middle| \ y= \frac{9}{\sqrt{x^2-3x-4}} \right\} r 2 = { ( x , y ) ∈ R × R y = x 2 − 3 x − 4 9 } แล้ว D r 1 ∩ D r 2 D_{r_1} \cap D_{r_2} D r 1 ∩ D r 2
[ − 3 , − 1 ) ∪ ( 4 , 97 ] [-3, -1) \cup (4, 97] [ − 3 , − 1 ) ∪ ( 4 , 97 ] [ − 3 , − 1 ) ∪ ( 3 , 97 ] [-3, -1) \cup (3, 97] [ − 3 , − 1 ) ∪ ( 3 , 97 ] [ − 3 , − 1 ) [-3, -1) [ − 3 , − 1 ) ( 3 , 97 ] (3, 97] ( 3 , 97 ] ( 4 , 97 ] (4, 97] ( 4 , 97 ] วิธีทำ
(1) พิจารณาโดเมนของ r 1 r_1 r 1 เนื่องจาก 10 − x + 3 ≥ 0 10 - \sqrt{x+3} \geq 0 10 − x + 3 ≥ 0 10 ≥ x + 3 10 \geq \sqrt{x+3} 10 ≥ x + 3 100 ≥ ∣ x + 3 ∣ 100 \geq \left| x+3 \right| 100 ≥ ∣ x + 3 ∣ เพราะฉะนั้น ∣ x + 3 ∣ ≤ 100 \left| x+3 \right| \leq 100 ∣ x + 3 ∣ ≤ 100 − 100 ≤ x + 3 ≤ 100 -100 \leq x+3 \leq 100 − 100 ≤ x + 3 ≤ 100 − 103 ≤ x ≤ 97 -103 \leq x \leq 97 − 103 ≤ x ≤ 97 แต่เนื่องจาก x + 3 ≥ 0 x+3 \geq 0 x + 3 ≥ 0 x ≥ − 3 x \geq -3 x ≥ − 3 ดังนั้น D r 1 = [ − 3 , 97 ] D_{r_1} = [-3, 97] D r 1 = [ − 3 , 97 ]
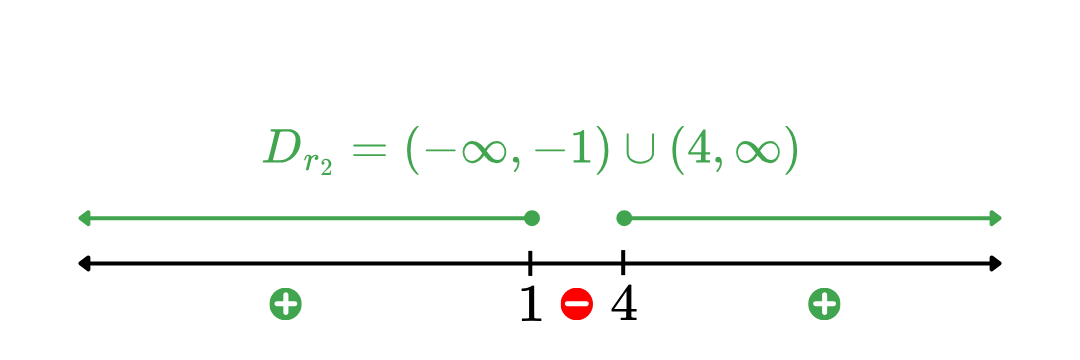
(2) พิจารณาโดเมนของ r 2 r_2 r 2 เนื่องจาก x 2 − 3 x − 4 ≠ 0 \sqrt{x^2-3x-4} \neq 0 x 2 − 3 x − 4 = 0 x 2 − 3 x − 4 ≠ 0 x^2-3x-4 \neq 0 x 2 − 3 x − 4 = 0 ทำให้ได้ว่า ( x − 4 ) ( x + 1 ) ≠ 0 (x-4)(x+1) \neq 0 ( x − 4 ) ( x + 1 ) = 0 x ≠ 4 , − 1 x \neq 4, -1 x = 4 , − 1 แต่เนื่องจาก x 2 − 3 x − 4 ≥ 0 x^2-3x-4 \geq 0 x 2 − 3 x − 4 ≥ 0 ( x − 4 ) ( x + 1 ) ≥ 0 (x-4)(x+1) \geq 0 ( x − 4 ) ( x + 1 ) ≥ 0 ดังนั้น D r 2 = ( − ∞ , − 1 ) ∪ ( 4 , ∞ ) D_{r_2} = (-\infty, -1) \cup (4, \infty) D r 2 = ( − ∞ , − 1 ) ∪ ( 4 , ∞ )
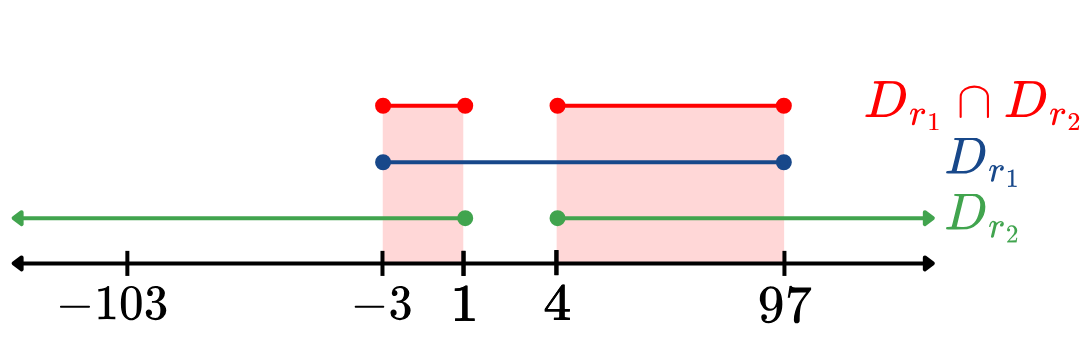
(3) หา D r 1 ∩ D r 2 D_{r_1} \cap D_{r_2} D r 1 ∩ D r 2
เพราะฉะนั้น D r 1 ∩ D r 2 = [ − 3 , − 1 ) ∪ ( 4 , 97 ] D_{r_1} \cap D_{r_2} = [-3, -1) \cup (4, 97] D r 1 ∩ D r 2 = [ − 3 , − 1 ) ∪ ( 4 , 97 ]
ตอบ ข้อ 1. [ − 3 , − 1 ) ∪ ( 4 , 97 ] [-3, -1) \cup (4, 97] [ − 3 , − 1 ) ∪ ( 4 , 97 ]