สวัสดีค้าบบ^^ วันนี้พี่หมอแม็คจะมาสปอยหนังเดอะ เมทริกซ์ กันนะครับ แฮร่ๆ ไม่ใช่แล้วๆ 55555 เดี๋ยววันนี้พี่แม็คจะสรุปเนื้อหาความรู้ สาระสำคัญในบทเมทริกซ์ให้เข้าใจสั้น ๆ และง่าย ๆ ดังนี้ค้าบบ
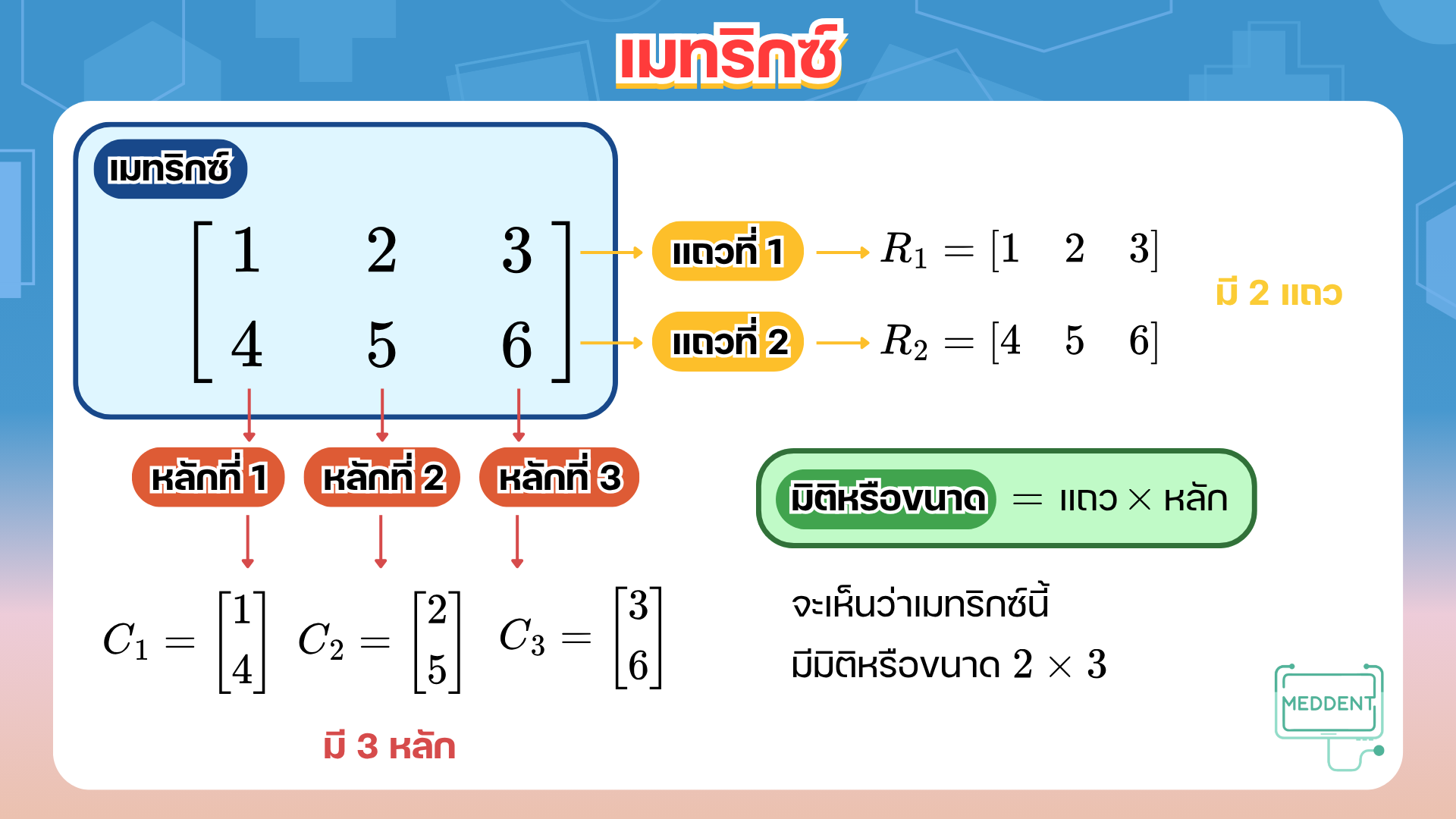
เมทริกซ์ เป็นการเขียนสมาชิกที่อยู่ในรูปคล้ายตารางที่ไม่มีเส้น สำหรับสมาชิกที่เขียนในแนวนอน เรียกว่า แถว และสมาชิกที่เขียนในแนวตั้ง เรียกว่า หลัก ซึ่งเมทริกซ์นี้จะมีขนาดหรือมิติเท่ากับ จำนวนแถว × \times ×
จากตัวอย่างของเมทริกซ์ข้างบน น้อง ๆ จะเห็นว่า เมทริกซ์ [ 1 2 3 4 5 6 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} [ 1 4 2 5 3 6 ] 2 × 3 2 \times 3 2 × 3
นอกจากนี้ยังใช้สัญลักษณ์ R 1 R_1 R 1 R 1 = [ 1 2 3 ] R_1 = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} R 1 = [ 1 2 3 ] และ R 2 R_2 R 2 R 2 = [ 4 5 6 ] R_2 = \begin{bmatrix} 4 & 5 & 6 \end{bmatrix} R 2 = [ 4 5 6 ]
สำหรับสัญลักษณ์ C 1 C_1 C 1 C 1 = [ 1 4 ] C_1 = \begin{bmatrix} 1 \\ 4 \end{bmatrix} C 1 = [ 1 4 ] C 2 C_2 C 2 C 2 = [ 2 5 ] C_2 = \begin{bmatrix} 2 \\ 5 \end{bmatrix} C 2 = [ 2 5 ] และ C 3 C_3 C 3 C 1 = [ 3 6 ] C_1 = \begin{bmatrix} 3 \\ 6 \end{bmatrix} C 1 = [ 3 6 ]
เมทริกซ์สามารถเขียนแทนด้วยตัวอักษรภาษาอังกฤษตัวพิมพ์ใหญ่ ได้แก่ A , B , C , … A, B, C, \ldots A , B , C , … สำหรับสมาชิกในแถวที่ i i i j j j a i j a_{ij} a ij Ex. ให้ A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A = [ 1 4 2 5 3 6 ] a 13 a_{13} a 13 a 13 = 3 a_{13} = 3 a 13 = 3
เมทริกซ์ A A A B B B A = B A = B A = B Ex. 1. A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A = [ 1 4 2 5 3 6 ] B = [ 1 2 3 4 5 6 ] B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} B = [ 1 4 2 5 3 6 ] จะเห็นว่า เมทริกซ์ A A A B B B
2. A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A = [ 1 4 2 5 3 6 ] B = [ 1 2 5 4 3 6 ] B = \begin{bmatrix} 1 & 2 & 5 \\ 4 & 3 & 6 \end{bmatrix} B = [ 1 4 2 3 5 6 ] จะเห็นว่า เมทริกซ์ A A A B B B a 22 = 5 ≠ 3 = b 22 a_{22} = 5 \neq 3 = b_{22} a 22 = 5 = 3 = b 22
3. A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A = [ 1 4 2 5 3 6 ] B = [ 1 2 3 4 5 6 ] B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} B = 1 3 5 2 4 6 จะเห็นว่า เมทริกซ์ A A A B B B A A A 2 × 3 2 \times 3 2 × 3 B B B 3 × 2 3 \times 2 3 × 2
กำหนดให้ A A A B B B c c c การบวกของเมทริกซ์: A + B A + B A + B การลบของเมทริกซ์: A − B A - B A − B การคูณเมทริกซ์ด้วยค่าคงที่: c A cA c A c c c
Ex. ให้ A = [ − 2 1 4 − 3 0 − 2 ] A = \begin{bmatrix} -2 & 1 & 4 \\ -3 & 0 & -2 \end{bmatrix} A = [ − 2 − 3 1 0 4 − 2 ] B = [ 1 0 − 2 − 3 7 1 ] B = \begin{bmatrix} 1 & 0 & -2 \\ -3 & 7 & 1 \end{bmatrix} B = [ 1 − 3 0 7 − 2 1 ] A + B , A − B , 3 A A+B, A-B, 3A A + B , A − B , 3 A 0 B 0B 0 B วิธีทำ A + B = [ − 2 1 4 − 3 0 − 2 ] + [ 1 0 − 2 − 3 7 1 ] = [ − 1 1 2 − 6 7 − 1 ] A + B = \begin{bmatrix} -2 & 1 & 4 \\ -3 & 0 & -2 \end{bmatrix} + \begin{bmatrix} 1 & 0 & -2 \\ -3 & 7 & 1 \end{bmatrix} = \begin{bmatrix} -1 & 1 & 2 \\ -6 & 7 & -1 \end{bmatrix} A + B = [ − 2 − 3 1 0 4 − 2 ] + [ 1 − 3 0 7 − 2 1 ] = [ − 1 − 6 1 7 2 − 1 ]
A − B = [ − 2 1 4 − 3 0 − 2 ] − [ 1 0 − 2 − 3 7 1 ] = [ − 3 1 6 0 − 7 − 3 ] A - B = \begin{bmatrix} -2 & 1 & 4 \\ -3 & 0 & -2 \end{bmatrix} - \begin{bmatrix} 1 & 0 & -2 \\ -3 & 7 & 1 \end{bmatrix} = \begin{bmatrix} -3 & 1 & 6 \\ 0 & -7 & -3 \end{bmatrix} A − B = [ − 2 − 3 1 0 4 − 2 ] − [ 1 − 3 0 7 − 2 1 ] = [ − 3 0 1 − 7 6 − 3 ]
3 A = 3 [ − 2 1 4 − 3 0 − 2 ] = [ − 6 3 12 − 9 0 − 6 ] 3A = 3 \begin{bmatrix} -2 & 1 & 4 \\ -3 & 0 & -2 \end{bmatrix} = \begin{bmatrix} -6 & 3 & 12 \\ -9 & 0 & -6 \end{bmatrix} 3 A = 3 [ − 2 − 3 1 0 4 − 2 ] = [ − 6 − 9 3 0 12 − 6 ]
0 B = 0 [ 1 0 − 2 − 3 7 1 ] = [ 0 0 0 0 0 0 ] 0B = 0 \begin{bmatrix} 1 & 0 & -2 \\ -3 & 7 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} 0 B = 0 [ 1 − 3 0 7 − 2 1 ] = [ 0 0 0 0 0 0 ]
ต่อไปเป็นการดำเนินการอีกอย่างบนเมทริกซ์ นั่นคือ การคูณเมทริกซ์ด้วยเมทริกซ์ ซึ่งการที่น้อง ๆ จะคูณเมทริกซ์ด้วยเมทริกซ์ได้ สิ่งที่สำคัญที่สุดเลยน้อง ๆ จะต้องเช็คขนาดของเมทริกซ์ก่อนต้องเป็นไปตามเงื่อนไขที่กำหนดก่อน แล้วค่อยคูณเมทริกซ์ด้วยเมทริกซ์ได้เลยครับ ^^
การคูณเมทริกซ์ด้วยเมทริกซ์ STEP 1 STEP 2
Ex. ให้ A = [ − 2 1 4 − 3 0 − 2 ] A = \begin{bmatrix} -2 & 1 & 4 \\ -3 & 0 & -2 \end{bmatrix} A = [ − 2 − 3 1 0 4 − 2 ] B = [ 1 0 − 2 − 3 7 1 ] B = \begin{bmatrix} 1 & 0 & -2 \\ -3 & 7 & 1 \end{bmatrix} B = [ 1 − 3 0 7 − 2 1 ] A B AB A B วิธีทำ เนื่องจาก A A A 2 × 3 2 \times 3 2 × 3 3 3 3 B B B 2 × 3 2 \times 3 2 × 3 2 2 2 A B AB A B
Ex. ให้ A = [ 1 − 2 0 3 ] A = \begin{bmatrix} 1 & -2 \\ 0 & 3 \end{bmatrix} A = [ 1 0 − 2 3 ] B = [ 4 5 − 1 2 ] B = \begin{bmatrix} 4 & 5 \\ -1 & 2 \end{bmatrix} B = [ 4 − 1 5 2 ] A B AB A B วิธีทำ เนื่องจาก A A A 2 × 2 2 \times 2 2 × 2 2 2 2 B B B 2 × 2 2 \times 2 2 × 2 2 2 2 A B AB A B A B AB A B
เมทริกซ์สลับเปลี่ยน (transpose matrix) ของเมทริกซ์ A A A A t A^t A t A A A
Ex. 1. ให้ A = [ 1 2 3 4 5 6 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} A = [ 1 4 2 5 3 6 ] A t = [ 1 4 2 5 3 6 ] A^t = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix} A t = 1 2 3 4 5 6 2. ให้ B = [ − 3 1 4 − 2 1 3 0 1 − 7 ] B = \begin{bmatrix} -3 & 1 & 4 \\ -2 & 1 & 3 \\ 0 & 1 & -7 \end{bmatrix} B = − 3 − 2 0 1 1 1 4 3 − 7 B t = [ − 3 − 2 0 1 1 1 4 3 − 7 ] B^t = \begin{bmatrix} -3 & -2 & 0 \\ 1 & 1 & 1 \\ 4 & 3 & -7 \end{bmatrix} B t = − 3 1 4 − 2 1 3 0 1 − 7
เมทริกซ์จัตุรัส คือ เมทริกซ์ที่มีจำนวนแถวและจำนวนหลักเท่ากัน และเรียกสมาชิกในตำแหน่งของแถวตรงกับตำแหน่งของหลักว่า สมาชิกบนเส้นทแยงมุมหลัก
Ex. 1. ให้ A = [ 1 2 4 5 ] A = \begin{bmatrix} 1 & 2 \\ 4 & 5 \end{bmatrix} A = [ 1 4 2 5 ] 1 1 1 5 5 5 2. ให้ B = [ − 3 1 4 − 2 1 3 0 1 − 7 ] B = \begin{bmatrix} -3 & 1 & 4 \\ -2 & 1 & 3 \\ 0 & 1 & -7 \end{bmatrix} B = − 3 − 2 0 1 1 1 4 3 − 7 − 3 , 1 -3, 1 − 3 , 1 − 7 -7 − 7
Ex. 1. ให้ A = [ 1 2 4 5 ] A = \begin{bmatrix} 1 & 2 \\ 4 & 5 \end{bmatrix} A = [ 1 4 2 5 ] det ( A ) = 1 ⋅ 5 − 4 ⋅ 2 = − 3 \det(A) = 1 \cdot 5 - 4 \cdot 2 = -3 det ( A ) = 1 ⋅ 5 − 4 ⋅ 2 = − 3 2. ให้ B = [ − 3 1 4 − 2 1 3 0 1 − 7 ] B = \begin{bmatrix} -3 & 1 & 4 \\ -2 & 1 & 3 \\ 0 & 1 & -7 \end{bmatrix} B = − 3 − 2 0 1 1 1 4 3 − 7 จะได้ว่า det ( B ) = ∣ − 3 1 4 − 2 1 3 0 1 − 7 ∣ − 3 1 − 2 1 0 1 = 21 + 0 + ( − 8 ) − 0 − ( − 9 ) − 14 = 8 \det(B) = \begin{vmatrix} -3 & 1 & 4 \\ -2 & 1 & 3 \\ 0 & 1 & -7 \end{vmatrix}\begin{matrix} -3 & 1 \\ -2 & 1 \\ 0 & 1 \end{matrix} = 21 + 0 + (-8) - 0 - (-9) - 14 = 8 det ( B ) = − 3 − 2 0 1 1 1 4 3 − 7 − 3 − 2 0 1 1 1 = 21 + 0 + ( − 8 ) − 0 − ( − 9 ) − 14 = 8
ก่อนที่จะเริ่มหัวข้อเมทริกซ์ผกผัน พี่แม็คจะให้เทคนิคที่สำคัญเกี่ยวกับการคูณเมทริกซ์ด้วยเมทริกซ์ ซึ่งจำเป็นที่น้อง ๆ จะต้องรู้ก่อน นั่นคือ เมทริกซ์เอกลักษณ์ ดังนี้
เมทริกซ์เอกลักษณ์ขนาด n × n n\times n n × n I n I_n I n n × n n\times n n × n 1 1 1 0 0 0 TIPS สำหรับเมทริกซ์ A A A m × n m \times n m × n A I n = A AI_n=A A I n = A I m A = A I_mA=A I m A = A
ต่อไปพี่แม็คจะพาน้อง ๆ มาหาเมทริกซ์ผกผันกัน ให้ A A A n × n n \times n n × n B B B A A A I n I_n I n B B B n × n n \times n n × n B B B A A A
Ex. 1.ให้ A = [ 1 2 4 5 ] A = \begin{bmatrix} 1 & 2 \\ 4 & 5 \end{bmatrix} A = [ 1 4 2 5 ] det ( A ) = 1 ⋅ 5 − 4 ⋅ 2 = − 3 \det(A) = 1 \cdot 5 - 4 \cdot 2 = -3 det ( A ) = 1 ⋅ 5 − 4 ⋅ 2 = − 3 ทำให้ A − 1 = 1 det ( A ) [ 5 − 2 − 4 1 ] = 1 8 [ 5 − 2 − 4 1 ] A^{-1} = \displaystyle\frac{1}{\det(A)} \begin{bmatrix} 5 & -2 \\ -4 & 1 \end{bmatrix} = \displaystyle\frac{1}{8} \begin{bmatrix} 5 & -2 \\ -4 & 1 \end{bmatrix} A − 1 = det ( A ) 1 [ 5 − 4 − 2 1 ] = 8 1 [ 5 − 4 − 2 1 ] นั่นคือ A − 1 = [ 5 8 − 2 8 − 4 8 1 8 ] A^{-1} = \begin{bmatrix} \displaystyle\frac{5}{8} & -\displaystyle\frac{2}{8} \\ -\displaystyle\frac{4}{8} & \displaystyle\frac{1}{8} \end{bmatrix} A − 1 = 8 5 − 8 4 − 8 2 8 1
2. ให้ B = [ − 2 3 − 4 6 ] B = \begin{bmatrix} -2 & 3 \\ -4 & 6 \end{bmatrix} B = [ − 2 − 4 3 6 ] det ( B ) = ( − 2 ) ⋅ 6 − ( − 4 ) ⋅ 3 = − 12 + 12 = 0 \det(B) = (-2) \cdot 6 - (-4) \cdot 3 = -12 + 12 = 0 det ( B ) = ( − 2 ) ⋅ 6 − ( − 4 ) ⋅ 3 = − 12 + 12 = 0 ดังนั้น เมทริกซ์ผกผันของเมทริกซ์ B B B
รูปแบบคำตอบของระบบสมการเชิงเส้น ระบบสมการเชิงเส้นมีเพียงคำตอบเดียว ระบบสมการเชิงเส้นมีคำตอบเป็นอนันต์ ระบบสมการเชิงเส้นไม่มีคำตอบ การหาคำตอบของระบบสมการเชิงเส้นน้อง ๆ อาจเคยคุ้นเคยกับการแก้ระบบสมการมาบ้างแล้ว เช่น การวาดกราฟ การกำจัดตัวแปร หรือแม้แต่การจัดรูปของสมการแล้วนำมาหักล้างกัน ซึ่งน้อง ๆ สามารถแก้ระบบสมการโดยใช้วิธีดังกล่าวก็ได้ แต่วิธีการที่พี่แม็คจะพูดถึงต่อไปนี้เป็นวิธีการแก้ระบบสมการแบบใหม่ ซึ่งน้อง ๆ สามารถทำได้ 2 แบบ คือ การคูณด้วยเมทริกซ์ผกผัน และการใช้เมทริกซ์แต่งเติม เรามาดูกันผ่านตัวอย่างต่อไปนี้กันได้เลยคั้บ
การแก้ระบบสมการเชิงเส้นโดยใช้เมทริกซ์ผกผัน จากสมการเมทริกซ์ A X = B AX=B A X = B A − 1 A = I A^{-1}A = I A − 1 A = I A A − 1 = I AA^{-1} = I A A − 1 = I เมื่อคูณ A − 1 A^{-1} A − 1 A X = B AX=B A X = B A − 1 A X = A − 1 B A^{-1}AX= A^{-1}B A − 1 A X = A − 1 B I X = A − 1 B IX = A^{-1}B I X = A − 1 B X = A − 1 B X= A^{-1}B X = A − 1 B ดังนั้น ถ้า A A A X = A − 1 B X= A^{-1}B X = A − 1 B
Ex. จงหาคำตอบของระบบสมการเชิงเส้น
x + y = 8 2 x − y = 7 \begin{align*} x+y &= 8 \\ 2x-y &= 7 \end{align*} x + y 2 x − y = 8 = 7
วิธีทำ กำหนดให้ A = [ 1 1 2 − 1 ] , X = [ x y ] A = \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix}, X = \begin{bmatrix} x \\ y \end{bmatrix} A = [ 1 2 1 − 1 ] , X = [ x y ] B = [ 8 7 ] B = \begin{bmatrix} 8 \\ 7 \end{bmatrix} B = [ 8 7 ] A X = B AX=B A X = B [ 1 1 2 − 1 ] [ x y ] = [ 8 7 ] \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 8 \\ 7 \end{bmatrix} [ 1 2 1 − 1 ] [ x y ] = [ 8 7 ]
เนื่องจาก A = [ 1 1 2 − 1 ] A = \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix} A = [ 1 2 1 − 1 ] det ( A ) = ∣ 1 1 2 − 1 ∣ = − 1 − 2 = − 3 \det(A) = \begin{vmatrix} 1 & 1 \\ 2 & -1 \end{vmatrix} = -1 - 2 = -3 det ( A ) = 1 2 1 − 1 = − 1 − 2 = − 3 จะได้ว่า A − 1 = 1 − 3 [ − 1 − 1 − 2 1 ] = [ 1 3 1 3 2 3 − 1 3 ] A^{-1} = \frac{1}{-3} \begin{bmatrix} -1 & -1 \\ -2 & 1 \end{bmatrix} = \begin{bmatrix} \displaystyle\frac{1}{3} & \displaystyle\frac{1}{3} \\ \displaystyle\frac{2}{3} & -\displaystyle\frac{1}{3} \end{bmatrix} A − 1 = − 3 1 [ − 1 − 2 − 1 1 ] = 3 1 3 2 3 1 − 3 1
ต่อไปจะหาคำตอบของระบบสมการเชิงเส้นโดยใช้เมทริกซ์ผกผัน ดังนี้
X = A − 1 B = [ 1 3 1 3 2 3 − 1 3 ] [ 8 7 ] = [ 8 + 7 3 16 − 7 3 ] = [ 5 3 ] X = A^{-1}B = \begin{bmatrix} \displaystyle\frac{1}{3} & \displaystyle\frac{1}{3} \\ \displaystyle\frac{2}{3} & -\displaystyle\frac{1}{3} \end{bmatrix} \begin{bmatrix} 8 \\ 7 \end{bmatrix} = \begin{bmatrix} \displaystyle\frac{8 + 7}{3} \\ \displaystyle\frac{16 - 7}{3} \end{bmatrix} = \begin{bmatrix} 5 \\ 3 \end{bmatrix} X = A − 1 B = 3 1 3 2 3 1 − 3 1 [ 8 7 ] = 3 8 + 7 3 16 − 7 = [ 5 3 ]
ดังนั้น ( 5 , 3 ) (5,3) ( 5 , 3 )
การแก้ระบบสมการเชิงเส้นโดยใช้เมทริกซ์แต่งเติม เมทริกซ์แต่งเติม คือ เมทริกซ์ [ A ∣ B ] [A\ |\ B] [ A ∣ B ]
การสลับแถวที่ i i i j j j R i ↔ R j R_i \leftrightarrow R_j R i ↔ R j คูณค่าคงที่ c c c i i i c R i cR_i c R i บวกแถวที่ i i i c c c j j j R i + c R j R_i + cR_j R i + c R j ถ้าเมทริกซ์ [ A ∣ B ] [A\ |\ B] [ A ∣ B ] [ C ∣ D ] [C\ |\ D] [ C ∣ D ] แล้วเมทริกซ์ [ A ∣ B ] [A\ |\ B] [ A ∣ B ] [ C ∣ D ] [C\ |\ D] [ C ∣ D ] [ A ∣ B ] ∼ [ C ∣ D ] [A\ |\ B] \sim [C\ |\ D] [ A ∣ B ] ∼ [ C ∣ D ]
โดยการแก้ระบบสมการเชิงเส้นเป้าหมายของเราก็คือ น้อง ๆ จะต้องเปลี่ยนเมทริกซ์ A A A [ A ∣ B ] [A\ |\ B] [ A ∣ B ] I I I [ I ∣ Z ] [I\ |\ Z] [ I ∣ Z ] Z Z Z
Ex. จงหาคำตอบของระบบสมการเชิงเส้น
x + y = 8 2 x − y = 7 \begin{align*} x+y &= 8 \\ 2x-y &= 7 \end{align*} x + y 2 x − y = 8 = 7
วิธีทำ กำหนดให้ A = [ 1 1 2 − 1 ] , X = [ x y ] A = \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix}, X = \begin{bmatrix} x \\ y \end{bmatrix} A = [ 1 2 1 − 1 ] , X = [ x y ] B = [ 8 7 ] B = \begin{bmatrix} 8 \\ 7 \end{bmatrix} B = [ 8 7 ] A X = B AX=B A X = B
[ 1 1 8 2 − 1 7 ] ∼ [ 1 1 8 0 − 3 − 9 ] R 2 − 2 R 1 ∼ [ 1 1 8 0 1 3 ] − 1 3 R 2 ∼ [ 1 0 5 0 1 3 ] R 1 − R 2 \begin{array}{rl} \left[ \begin{array}{cc|c} 1 & 1 & 8 \\ 2 & -1 & 7 \end{array} \right] &\sim \ \left[ \begin{array}{cc|c} 1 & 1 & 8 \\ 0 & -3 & -9 \end{array} \right] \begin{matrix} \\ R_2 - 2R_1 \end{matrix}\\ &\sim \ \left[ \begin{array}{cc|c} 1 & 1 & 8 \\ 0 & 1 & 3 \end{array} \right] \begin{matrix} \\ -\displaystyle\frac{1}{3}R_2 \end{matrix}\\ &\sim \left[ \begin{array}{cc|c} 1 & 0 & 5 \\ 0 & 1 & 3 \end{array} \right] \begin{matrix} R_1 - R_2 \\ \ \end{matrix} \end{array} [ 1 2 1 − 1 8 7 ] ∼ [ 1 0 1 − 3 8 − 9 ] R 2 − 2 R 1 ∼ [ 1 0 1 1 8 3 ] − 3 1 R 2 ∼ [ 1 0 0 1 5 3 ] R 1 − R 2
ดังนั้น ( 5 , 3 ) (5,3) ( 5 , 3 )
กำหนดเมทริกซ์แต่งเติมของระบบสมการระบบหนึ่งคือ [ 1 1 − 1 − 3 1 2 − 2 − 4 1 1 0 2 ] \left[ \begin{array}{rrr|r} 1 & 1 & -1 & -3 \\ 1 & 2 & -2 & -4 \\ 1 & 1 & 0 & 2 \end{array} \right] 1 1 1 1 2 1 − 1 − 2 0 − 3 − 4 2 ใช้การดำเนินการตามแถวเพื่อแปลงเมทริกซ์แต่งเติมนี้ให้ได้ [ 1 1 − 1 a 0 1 − 1 b 0 0 1 c ] \left[ \begin{array}{rrr|r} 1 & 1 & -1 & a \\ 0 & 1 & -1 & b \\ 0 & 0 & 1 & c \end{array} \right] 1 0 0 1 1 0 − 1 − 1 1 a b c a , b a, b a , b c c c ถ้า X = [ 1 1 1 1 a b 1 c 0 ] X = \begin{bmatrix} 1 & 1 & 1 \\ 1 & a & b \\ 1 & c & 0 \end{bmatrix} X = 1 1 1 1 a c 1 b 0 det ( 2 X t ) \det(2X^t) det ( 2 X t )
12 12 12 18 18 18 24 24 24 72 72 72 96 96 96 วิธีทำ
[ 1 1 − 1 − 3 1 2 − 2 − 4 1 1 0 2 ] ∼ [ 1 1 − 1 − 3 0 1 − 1 − 1 0 0 1 5 ] R 2 − R 1 R 3 − R 1 \begin{array}{rl} \left[ \begin{array}{rrr|r} 1 & 1 & -1 & -3 \\ 1 & 2 & -2 & -4 \\ 1 & 1 & 0 & 2 \end{array} \right] \sim\ \left[ \begin{array}{rrr|r} 1 & 1 & -1 & -3 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 1 & 5 \end{array} \right] & \begin{matrix} \\ R_2 - R_1 \\ R_3 - R_1 \end{matrix} \end{array} 1 1 1 1 2 1 − 1 − 2 0 − 3 − 4 2 ∼ 1 0 0 1 1 0 − 1 − 1 1 − 3 − 1 5 R 2 − R 1 R 3 − R 1
ดังนั้น a = − 3 , b = − 1 a = -3, b= -1 a = − 3 , b = − 1 c = 5 c = 5 c = 5
ต่อไปจะหาดีเทอร์มิแนนต์ของเมทริกซ์ 2 X t 2X^t 2 X t เนื่องจาก X = [ 1 1 1 1 − 3 − 1 1 5 0 ] X = \begin{bmatrix} 1 & 1 & 1 \\ 1 & -3 & -1 \\ 1 & 5 & 0 \end{bmatrix} X = 1 1 1 1 − 3 5 1 − 1 0 X t = [ 1 1 1 1 − 3 5 1 − 1 0 ] X^t = \begin{bmatrix} 1 & 1 & 1 \\ 1 & -3 & 5 \\ 1 & -1 & 0 \end{bmatrix} X t = 1 1 1 1 − 3 − 1 1 5 0 2 X t = [ 2 2 2 2 − 6 10 2 − 2 0 ] 2X^t = \begin{bmatrix} 2 & 2 & 2 \\ 2 & -6 & 10 \\ 2 & -2 & 0 \end{bmatrix} 2 X t = 2 2 2 2 − 6 − 2 2 10 0 เพราะฉะนั้น det ( 2 X t ) = ∣ 2 2 2 2 − 6 10 2 − 2 0 ∣ 2 2 2 − 6 2 − 2 = 0 + 40 + ( − 8 ) − ( − 24 ) − ( − 40 ) − 0 = 96 \det(2X^t) = \begin{vmatrix} 2 & 2 & 2 \\ 2 & -6 & 10 \\ 2 & -2 & 0 \end{vmatrix} \begin{matrix} 2 & 2 \\ 2 & -6 \\ 2 & -2 \end{matrix} = 0 + 40 + (-8) - (-24) - (-40) - 0 = 96 det ( 2 X t ) = 2 2 2 2 − 6 − 2 2 10 0 2 2 2 2 − 6 − 2 = 0 + 40 + ( − 8 ) − ( − 24 ) − ( − 40 ) − 0 = 96
ตอบ