สวัสดีค้าบบ วันนี้พี่แม็คจะพาน้อง ๆ มาทำความรู้จักกับเนื้อหาสำคัญมาก ๆ อีกหนึ่งเรื่องในคณิตศาสตร์ นั่นก็คือ หลักการนับเบื้องต้นและความน่าจะเป็น นั่นเองค้าบบ โดยเรื่องนี้อยู่กับเราในชีวิตประจำวันค่อนข้างมากอย่างเช่น

การพยากรณ์อากาศ บางครั้งน้อง ๆ อาจจะเห็นแจ้งเตือนในโทรศัพท์ว่า "ฝนมีโอกาสตก 70%" น้อง ๆ หลายคนอาจจะแปลว่า ยังไงก็ต้องพกร่มแน่ ๆ บางคนอาจคิดว่า ฝนน่าจะตกตลอดทั้งวันเลยหรือเปล่า จริง ๆ แล้วตัวเลขแบบนี้มาจากการคำนวณความเป็นไปได้โดยใช้เรื่องหลักการนับและความน่าจะเป็นมาช่วยนั่นเองค้าบบ

หลักการนับเบื้องต้น

หลักการบวก

ในการทำงานอย่างหนึ่ง ถ้าสามารถแบ่งวิธีการทำงานออกเป็น $k$ กรณี โดยที่
กรณีที่ 1 สามารถทำได้ $n_1$ วิธี
กรณีที่ 2 สามารถทำได้ $n_2$ วิธี
$\vdots$
กรณีที่ $k$ สามารถทำได้ $n_k$ วิธี
ซึ่งวิธีการทำงานในทั้ง $k$ กรณีไม่ซ้ำซ้อนกัน และการทำงานในแต่ละกรณีทำให้งานเสร็จสมบูรณ์
แล้วจะสามารถทำงานนี้ได้ทั้งหมด $n_1+n_2+\cdots+n_k$ วิธี

Ex. การเดินทางของจอยจากบ้านไปโรงเรียนสามารถเดินทางโดยรถเมล์ได้ $5$ สาย หรือจอยจะเดินทางโดยรถไฟฟ้าได้ $2$ สาย จงหาว่าจอยสามารถเดินทางจากบ้านไปโรงเรียนได้กี่วิธี
วิธีทำ เนื่องจากจอยเดินทางโดยรถเมล์ได้ $5$ สาย และจอยเดินทางโดยรถไฟฟ้าได้ $2$ สาย
โดยหลักการบวก จะได้ว่า จอยจะสามารถเดินทางจากบ้านไปโรงเรียนได้ทั้งหมด $5+2=7$ แบบ

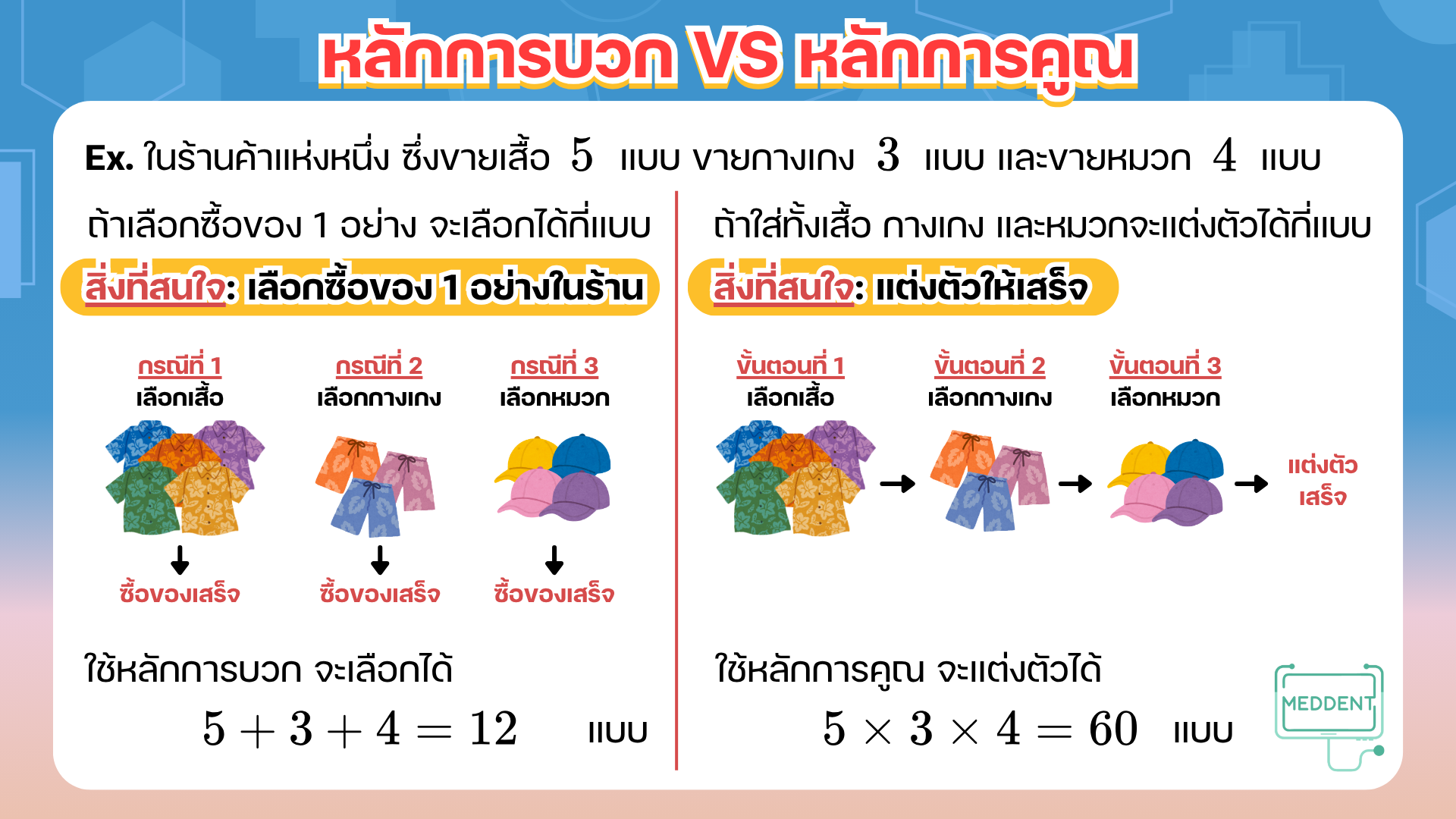
Ex. พี่แม็คกำลังตัดสินใจซื้อของในร้านค้าแห่งหนึ่ง ซึ่งขายเสื้อ $5$ แบบ ขายกางเกง $3$ แบบ และขายหมวก $4$ แบบ ถ้าพี่แม็คต้องการเลือกซื้อสินค้า $1$ ชิ้น จงหาว่าพี่แม็คจะเลือกซื้อของจากร้านค้าแห่งนี้ได้ทั้งหมดกี่แบบ
วิธีทำ เนื่องจากร้านค้ามีเสื้อ $5$ แบบ กางเกง $3$ แบบ และหมวก $4$ แบบ
โดยหลักการบวก จะได้ว่า พี่แม็คจะเลือกซื้อของจากร้านค้าแห่งนี้ได้ทั้งหมด $5+3+4=12$ แบบ

หลักการคูณ

ในการทำงานอย่างหนึ่ง ถ้าสามารถแบ่งขั้นตอนการทำงานออกเป็น $k$ ขั้นตอน ซึ่งต้องทำต่อเนื่องกัน โดยที่
ขั้นตอนที่ 1 เลือกทำได้ $n_1$ วิธี
ขั้นตอนที่ 2 เลือกทำได้ $n_2$ วิธี
$\vdots$
ขั้นตอนที่ $k$ เลือกทำได้ $n_k$ วิธี
แล้วจะสามารถทำงานนี้ได้ทั้งหมด $n_1\times n_2\times\cdots\times n_k$ วิธี

Ex. ในงานสัมมนาแห่งหนึ่งได้จัดของว่างให้กับผู้เข้าร่วม ซึ่งแบ่งเป็นขนมปังที่มีรสชาติที่แตกต่างกัน $4$ รส และเครื่องดื่มซึ่งเป็นน้ำผลไม้ที่มีรสชาติที่แตกต่างกัน $6$ รส ถ้าต้องการจัดของว่างให้มีทั้งขนมปังและเครื่องดื่มให้กับผู้เข้าร่วมสัมมนาจะสามารถจัดได้ทั้งหมดกี่แบบ
วิธีทำ เนื่องจากของว่างที่ต้องจัดจะมีขนมปัง $4$ รสชาติที่แตกต่างกัน และน้ำผลไม้ $6$ รสชาติที่แตกต่างกัน
โดยหลักการคูณ จะได้ว่า ของว่างจะสามารถจัดได้ทั้งหมด $4 \times 6 = 24$ แบบ

Ex. พี่แม็คกำลังแต่งตัวออกจากบ้าน ซึ่งมีเสื้อ $5$ แบบ กางเกง $3$ แบบ และหมวก $4$ แบบ ถ้าพี่แม็คต้องการแต่งตัวออกจากบ้านโดยใส่ทั้งเสื้อ กางเกง และหมวกอย่างละ $1$ ชิ้น จงหาว่าพี่แม็คจะแต่งตัวออกจากบ้านได้แตกต่างกันทั้งหมดกี่แบบ
วิธีทำ เนื่องจากพี่แม็คมีเสื้อ $5$ แบบ กางเกง $3$ แบบ และหมวก $4$ แบบ
โดยหลักการคูณ จะได้ว่า พี่แม็คจะแต่งตัวออกจากบ้านได้แตกต่างกันทั้งหมด $5 \times 3 \times 4 = 60$ แบบ

TIPS: หลักการบวกใช้เมื่อแต่ละกรณี ทำงานได้เสร็จสมบูรณ์
หลักการคูณใช้เมื่อขั้นตอนย่อย ๆ ทำงานยังไม่เสร็จสมบูรณ์

จากตัวอย่างที่ผ่านมาที่เป็นข้อที่พี่แม็คกำลังตัดสินใจซื้อเสื้อ กางเกง และหมวกมา 1 ชิ้น จะเห็นว่าการทำงานของพี่แม็ค คือ เลือกซื้อสิ่งของอะไรสักอย่างมา 1 ชิ้น จึงทำให้การทำงานนี้เสร็จสมบูรณ์ ทำให้ตัวอย่างนี้จะคิดโดยใช้หลักการบวก
แต่จะแตกต่างกับข้อที่พี่แม็คแต่งตัวออกจากบ้าน จะเห็นว่า การทำงานของพี่แม็ค คือ จะต้องเลือกทั้งเสื้อ กางเกง และหมวกมาอย่างละ 1 ชิ้น จึงจะทำให้พี่แม็คแต่งตัวเสร็จ แล้วออกจากบ้านได้ ทำให้ตัวอย่างนี้จะคิดโดยใช้หลักการคูณนั่นเองคร้าบบ

จะเห็นว่าภายใต้สถานการณ์เดียวกัน แต่การทำงานที่ให้ผลลัพธ์ที่แตกต่างกันจะส่งผลทำให้วิธีการคิดคำนวณที่ต่างกันออกไป ทั้งนี้ให้น้อง ๆ โฟกัสที่โจทย์เป็นหลักว่า โจทย์เขาต้องทำงานในรูปแบบใด น้องๆ อาจจะค่อยๆ ร่างแผนภาพคร่าว ๆ ว่าการทำงานนั้นต้องทำอะไรบ้าง ซึ่งจะช่วยให้น้อง ๆ เห็นภาพได้มากยิ่งขึ้นนั่นเองคร้าบบ

สำหรับตัวอย่างถัดไป พี่แม็คจะชวนน้อง ๆ มาดูให้เห็นเกี่ยวกับการนำไปใช้ของหลักการบวกและหลักการคูณร่วมกัน ดังนี้ค้าบบ

Ex. ต้องการสร้างจำนวนเต็มบวก $3$ หลักที่เป็นจำนวนคี่ที่มีค่ามากกว่า $200$ จากเลขโดด $0, 1, 2, 3, 4, 5$
โดยที่ตัวเลขในแต่ละหลักไม่ซ้ำกันจะสามารถสร้างได้ทั้งหมดกี่จำนวน
วิธีทำ การสร้างจำนวนเต็มบวก $3$ หลักที่เป็นจำนวนคี่ที่มีค่ามากกว่า $200$ สามารถพิจารณาได้เป็น $2$ กรณีดังนี้
กรณีที่ 1 เลขโดดในหลักร้อยเป็นจำนวนคู่
ขั้นตอนที่ 1 พิจารณาตัวเลขในหลักร้อยที่เป็นไปได้ทั้งหมด ได้แก่ $2, 4$ ซึ่งทำได้ $2$ วิธี
ขั้นตอนที่ 2 เนื่องจากจะสร้างจำนวนคี่ที่มีค่ามากกว่า $200$ แสดงว่าตัวเลขในหลักหน่วยที่เป็นไปได้ทั้งหมด ได้แก่ $1, 3, 5$ ซึ่งทำได้ $3$ วิธี
ขั้นตอนที่ 3 เนื่องจากจะสร้างจำนวนที่ตัวเลขในแต่ละหลักไม่ซ้ำกัน แสดงว่าตัวเลขในหลักสิบที่เป็นไปได้ทั้งหมดต้องเป็นตัวเลขที่ไม่ได้ใช้ทั้งหลักหน่วยและหลักร้อย ซึ่งทำได้ $4$ วิธี
โดยหลักการคูณ จะได้ว่า จำนวนเต็มบวก $3$ หลักที่เป็นจำนวนคี่ที่มีค่ามากกว่า $200$ โดยที่เลขโดดในหลักร้อยเป็นจำนวนคู่ ซึ่งมีทั้งหมด $2 \times 3 \times 4 = 24$ วิธี

กรณีที่ 2 เลขโดดในหลักร้อยเป็นจำนวนคี่
ขั้นตอนที่ 1 พิจารณาตัวเลขในหลักร้อยที่เป็นไปได้ทั้งหมด ได้แก่ $3, 5$ ซึ่งทำได้ $2$ วิธี
ขั้นตอนที่ 2 เนื่องจากจะสร้างจำนวนคี่ที่มีค่ามากกว่า $200$ และตัวเลขไม่ซ้ำกับหลักร้อย แสดงว่าตัวเลขในหลักหน่วยที่เป็นไปได้ทั้งหมดมี $2$ วิธี (นั่นคือ $1$ และตัวเลขอีกตัวที่ไม่ซ้ำกับหลักร้อย)
ขั้นตอนที่ 3 เนื่องจากจะสร้างจำนวนที่ตัวเลขในแต่ละหลักไม่ซ้ำกัน แสดงว่าตัวเลขในหลักสิบที่เป็นไปได้ทั้งหมดต้องเป็นตัวเลขที่ไม่ได้ใช้ทั้งหลักหน่วยและหลักร้อย ซึ่งทำได้ $4$ วิธี
โดยหลักการคูณ จะได้ว่า จำนวนเต็มบวก $3$ หลักที่เป็นจำนวนคี่ที่มีค่ามากกว่า $200$ โดยที่เลขโดดในหลักร้อยเป็นจำนวนคี่ ซึ่งมีทั้งหมด $2 \times 2 \times 4 = 16$ วิธี

จากทั้ง $2$ กรณี โดยหลักการบวก จะได้ว่า จำนวนเต็มบวก $3$ หลักที่เป็นจำนวนคี่ที่มีค่ามากกว่า $200$ มีทั้งหมด $24+16 = 40$ วิธี

จากตัวอย่างที่ผ่านมาการสร้างจำนวนเต็มบวก $3$ หลัก น้อง ๆ จะเห็นว่า พี่แม็คได้สร้างจำนวนโดยพิจารณาที่ตัวเลขในหลักร้อยก่อน แต่น้อง ๆ สามารถสร้างจำนวนโดยพิจารณาที่ตัวเลขในหลักหน่วยก่อนก็ได้ ซึ่งแบ่งได้เป็น $3$ กรณี นั่นคือ เลขโดดในหลักหน่วยเป็น $1, 3$ และ $5$ แล้วค่อยพิจารณาเลขโดยในหลักร้อยและหลักสิบตามลำดับ ซึ่งจะได้จำนวนวิธีเท่ากับ $16 + 12 + 12 = 40$ วิธีเช่นกัน

แฟกทอเรียล

$n! = 1 \times 2 \times \cdots \times n$ เมื่อ $n$ เป็นจำนวนเต็มบวก
และ $0! = 1$

Ex. ตัวอย่างของแฟกทอเรียล
$1! = 1$
$2! = 1 \times 2 = 2$
$3! = 1 \times 2 \times 3 = 6$
$4! = 1 \times 2 \times 3 \times 4 = 24$
$5! = 1 \times 2 \times 3 \times 4 \times 5 = 120$
$6! = 1 \times 2 \times 3 \times 4 \times 5 \times 6 = 720$

การเรียงสับเปลี่ยนเชิงเส้น

Ex. มีนักเรียน $5$ คน ต้องการเข้าแถวหน้ากระดานจะสามารถจัดเรียงได้ทั้งหมดกี่แบบ
วิธีทำ พิจารณาการเข้าแถวหน้ากระดานของนักเรียน $5$ คน ดังนี้
ขั้นตอนที่ 1 เลือกนักเรียนมาลงได้ $5$ คน
ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะเหลือคนที่ยังไม่ได้ยืนในแถว $4$ คน
ขั้นตอนที่ 3 จากขั้นตอนที่ 1 - 2 จะเหลือคนที่ยังไม่ได้ยืนในแถว $3$ คน
ขั้นตอนที่ 4 จากขั้นตอนที่ 1 - 3 จะเหลือคนที่ยังไม่ได้ยืนในแถว $2$ คน
ขั้นตอนที่ 5 จากขั้นตอนที่ 1 - 4 จะเหลือคนที่ยังไม่ได้ยืนในแถว $1$ คน
โดยหลักการคูณ จะได้ว่า การเข้าแถวหน้ากระดานของนักเรียน $5$ คนจะสามารถจัดเรียงได้ทั้งหมด
$5 \times 4 \times 3 \times 2 \times 1 = 120$ วิธี

จากตัวอย่างที่เรียงแถวหน้ากระดานของนักเรียน 5 คน น้อง ๆ สามารถทำได้โดยใช้หลักการคูณที่แสดงไว้ข้างต้นได้เลยคั้บ^^ แต่พี่แม็คสามารถมองตอบได้เลยทันทีว่ามีค่าเท่ากับ $5!$ เพราะ $5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$ นั่นเองคร้าบบ

Ex. มีนักเรียน $7$ คน ต้องการนั่งเก้าอี้ที่เรียงแถวหน้ากระดานจำนวน $5$ ที่นั่งจะสามารถจัดเรียงได้ทั้งหมดกี่แบบ
วิธีทำ พิจารณาการนั่งเข้าแถวหน้ากระดานของนักเรียน $7$ คน ดังนี้
ขั้นตอนที่ 1 เลือกนักเรียนมานั่งเก้าอี้ได้ $7$ คน
ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะเหลือนักเรียนมานั่งเก้าอี้อยู่ $6$ คน
ขั้นตอนที่ 3 จากขั้นตอนที่ 1 - 2 จะเหลือนักเรียนมานั่งเก้าอี้อยู่ $5$ คน
ขั้นตอนที่ 4 จากขั้นตอนที่ 1 - 3 จะเหลือนักเรียนมานั่งเก้าอี้อยู่ $4$ คน
ขั้นตอนที่ 5 จากขั้นตอนที่ 1 - 4 จะเหลือนักเรียนมานั่งเก้าอี้อยู่ $3$ คน
โดยหลักการคูณ จะได้ว่า การนั่งเก้าอี้ $5$ ที่นั่งที่เรียงแถวหน้ากระดานของนักเรียน $7$ คนจะสามารถจัดเรียงได้ทั้งหมด
$7 \times 6 \times 5 \times 4 \times 3 = 2520$ วิธี

จากตัวอย่างที่นำนักเรียน $7$ คน ต้องการนั่งเก้าอี้ที่เรียงแถวหน้ากระดานจำนวน $5$ ที่นั่ง พี่แม็คสามารถคิดได้อีกวิธี โดยนำนักเรียนทั้ง $7$ คนมาเรียงเป็นแถวตรงก่อน จะได้ทั้งหมด

\begin{align*} 7! = 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \end{align*}

แต่เราไม่ได้ต้องการให้นักเรียนทุกคนได้นั่งเก้าอี้ มีเพียง $5$ คนเท่านั้นที่ต้องเลือกมานั่ง และนักเรียนอีก $2$ คนที่เหลือ (ในที่นี้จะไม่นับรวมตำแหน่งของนักเรียน $2$ คนนั้น) ซึ่งพี่แม็คจะหารออกด้วย $2!$

จะได้ว่า การนั่งเก้าอี้ $5$ ที่นั่งที่เรียงแถวหน้ากระดานของนักเรียน $7$ คนจะสามารถจัดเรียงได้ทั้งหมด

\begin{align*} \displaystyle\frac{7!}{2!} &= \displaystyle\frac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1} \\ &= 7 \times 6 \times 5 \times 4 \times 3 \\ &= 2520 \end{align*}

ซึ่งรูปแบบการนับแบบนี้เรียกว่า การเรียงสับเปลี่ยนเชิงเส้น

การเรียงสับเปลี่ยนเชิงเส้น (linear permutation) ของสิ่งของ $r$ สิ่งจากทั้งหมด $n$ สิ่ง เขียนแทนด้วย $P_{n,r}$
กำหนดโดย

\begin{align*} P_{n,r} = \displaystyle\frac{n!}{(n-r)!} \end{align*}

จากตัวอย่างที่ผ่านมา ทำให้พี่แม็คสามารถสรุปได้เป็น 2 กรณี ดังนี้

การเรียงสับเปลี่ยนเชิงวงกลม

Ex. มีนักเรียน $5$ คน ต้องการนั่งโต๊ะกลมจะมีวิธีการนั่งทั้งหมดกี่แบบ
วิธีทำ พิจารณาการนั่งโต๊ะกลมของนักเรียน $5$ คน ดังนี้
กำหนดให้นักเรียน $5$ คนมีชื่อเป็น $A, B, C, D$ และ $E$
ขั้นตอนที่ 1 นำนักเรียน $A$ ลงมานั่งโต๊ะกลม ทำได้ $1$ วิธี
ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะสามารถนำ $B$ มานั่งลงเก้าอี้ได้ $4$ วิธี
ขั้นตอนที่ 3 จากขั้นตอนที่ 1 - 2 สามารถนำ $C$ มานั่งลงเก้าอี้ได้ $3$ วิธี
ขั้นตอนที่ 4 จากขั้นตอนที่ 1 - 3 สามารถนำ $D$ มานั่งลงเก้าอี้ได้ $2$ วิธี
ขั้นตอนที่ 5 จากขั้นตอนที่ 1 - 4 สามารถนำ $E$ มานั่งลงเก้าอี้ได้ $1$ วิธี
โดยหลักการคูณ จะได้ว่า การนั่งโต๊ะกลมของนักเรียน $5$ คนจะสามารถจัดเรียงได้ทั้งหมด
$1 \times 4 \times 3 \times 2 \times 1 = 24$ วิธี

ซึ่งรูปแบบการนับแบบนี้เรียกว่า การเรียงสับเปลี่ยนเชิงวงกลม (circular permutation)

จำนวนวิธีการเรียงสับเปลี่ยนเชิงวงกลมของสิ่งของที่แตกต่างกันทั้งหมด $n$ ชิ้น เท่ากับ $(n-1)!$ วิธี

การจัดหมู่

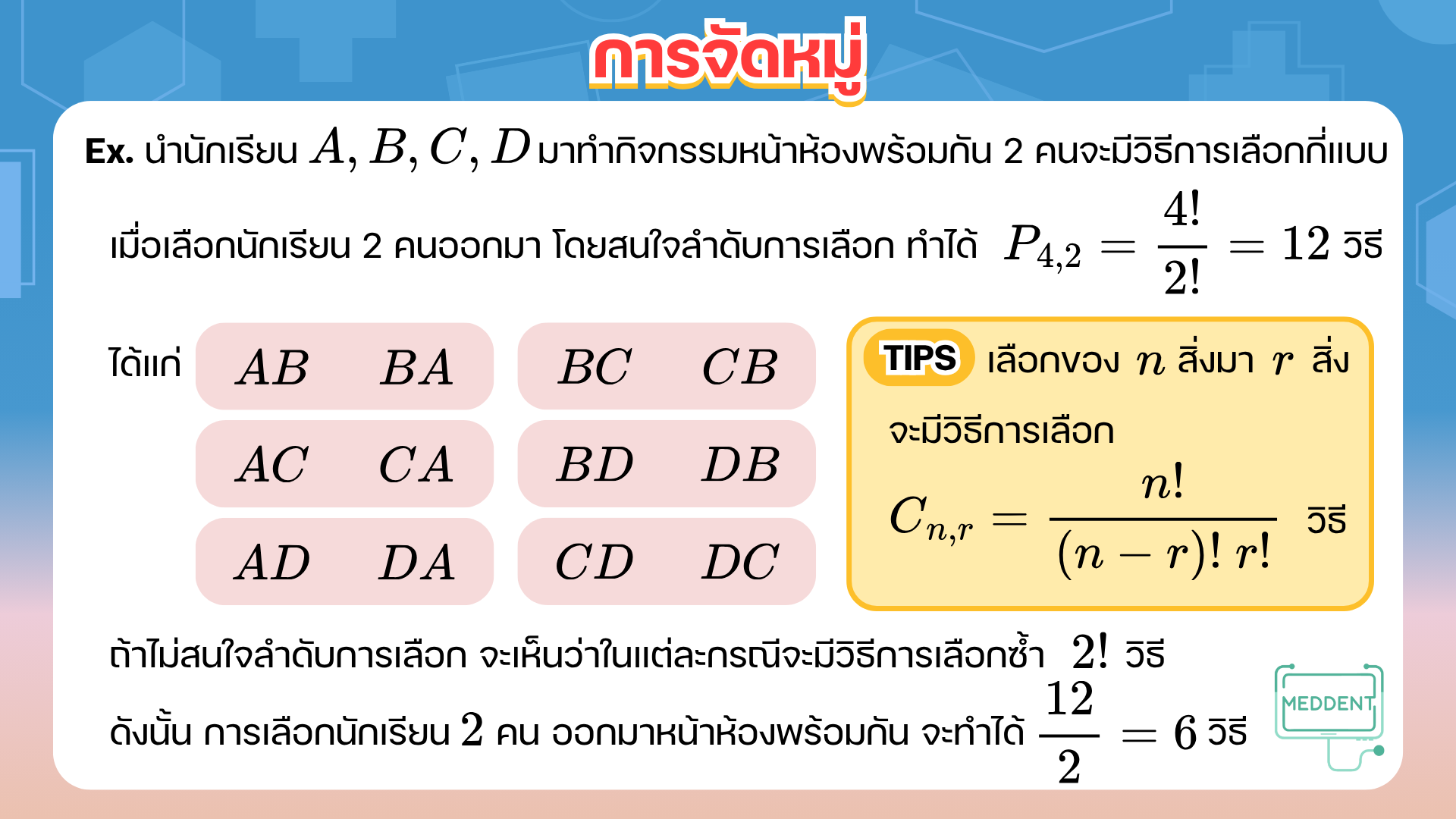
Ex. นำนักเรียน $A, B, C, D$ มาทำกิจกรรมหน้าห้องพร้อมกัน 2 คน จะมีวิธีการเลือกกี่แบบ
วิธีทำ พิจารณาการเลือกนักเรียน $2$ คนจากนักเรียน $4$ คน สามารถเลือกได้ดังนี้
ขั้นตอนที่ 1 เลือกนักเรียน $2$ คนจากนักเรียน $4$ คน ทำได้ $P_{4,2}$ วิธี
เนื่องจากการนำนักเรียนมาทำกิจกรรมหน้าชั้นเรียนในวิธีดังกล่าวจะสนใจลำดับการออกมาทำกิจกรรมหน้าชั้นเรียน
แต่ในที่นี้เราไม่ได้สนใจลำดับการเลือกนักเรียน ทำให้เกิดการนับซ้ำ เช่น $AB$ (A ออกก่อน B) และ $BA$ (B ออกก่อน A) จะเห็นว่าการเลือกนักเรียนนี้จะมี 2 คนนั่นคือ $A$ และ $B$ แต่แตกต่างกันตรงที่มีลำดับการออกมาทำกิจกรรม
โดยการนำนักเรียนมาทำกิจกรรม $2$ คน จะทำให้เกิดกรณีซ้ำทั้งหมด $2!$ วิธี
ดังนั้น การเลือกนักเรียน $2$ คน จากทั้งหมด $4$ คน จะทำได้ $\displaystyle\frac{P_{4,2}}{2!} = \frac{12}{2}= 6$ วิธี

ซึ่งรูปแบบการนับแบบนี้เรียกว่า การจัดหมู่ (combination)

จำนวนวิธีการเรียงสับเปลี่ยนเชิงวงกลมของสิ่งของที่แตกต่างกันทั้งหมด $n$ ชิ้น เขียนแทนด้วย $C_{n,r}$ หรือ $\begin{pmatrix} n \\ r \end{pmatrix}$ กำหนดโดย

\begin{align*} C_{n,r} = \displaystyle\frac{P_{n,r}}{n!} = \displaystyle\frac{n!}{(n-r)!\ r!} \end{align*}

ความน่าจะเป็น

แต่ก่อนอื่นพี่แม็คจะให้น้อง ๆ ทำความรู้จักกับการทดลองสุ่ม ปริภูมิตัวอย่าง และเหตุการณ์ ดังนี้
การทดลองสุ่ม (random experiment) คือ การทดลองที่ทราบว่ามีผลลัพธ์ที่เกิดขึ้นเป็นอะไรได้บ้าง แต่ไม่สามารถบอกได้ว่าในแต่ละครั้งที่ทดลองจะเกิดผลลัพธ์อะไรขึ้นมา
ปริภูมิตัวอย่าง (sample space) เขียนแทนด้วย $S$ คือ เซตของผลลัพธ์ที่เกิดขึ้นทั้งหมดจากการทดลองสุ่ม
เหตุการณ์ (event) เขียนแทนด้วย $E$ คือ สับเซตของปริภูมิตัวอย่าง

Ex. ตัวอย่างการทดลองสุ่ม ปริภูมิตัวอย่าง และเหตุการณ์

ในการโยนเหรียญ $1$ เหรียญ $1$ ครั้ง ผลลัพธ์ที่ได้จากการโยนเหรียญอาจจะเป็นหัว $(H)$ หรือก้อย $(T)$ ก็ได้
ปริภูมิตัวอย่าง คือ $S_1 =\left\{H,T\right\}$
ถ้าสนใจเหตุการณ์ที่เหรียญออกหัว จะได้ว่า เหตุการณ์ คือ $E_1=\left\{H\right\}$
ในการโยนลูกเต๋า $1$ ลูก $1$ ครั้ง ผลลัพธ์ที่ได้จากการโยนลูกเต๋าอาจจะเป็น $1,\ 2,\ 3,\ 4,\ 5$ หรือ $6$ ก็ได้
ปริภูมิตัวอย่าง คือ $S_2=\left\{1,\ 2,\ 3,\ 4,\ 5,\ 6\right\}$
ถ้าสนใจเหตุการณ์ที่ลูกเต๋าขึ้นแต้มเป็นจำนวนคู่ จะได้ว่า เหตุการณ์ คือ $E_2=\left\{2,\ 4,\ 6\right\}$

ความน่าจะเป็น (probability) เขียนแทนด้วย $P(E)$ เป็นอัตราส่วนของจำนวนเหตุการณ์ที่เกิดขึ้นต่อจำนวนเหตุการณ์ที่เกิดขึ้นทั้งหมด นั่นคือ

\begin{align*} P(E) = \displaystyle\frac{n(E)}{n(S)} \end{align*}

Ex. จงหาความน่าจะเป็นของการโยนลูกเต๋า $1$ ลูก $1$ ครั้งแล้วแต้มของลูกเต๋าออกมาน้อยกว่า $3$
วิธีทำ เนื่องจากปริภูมิตัวอย่างของการโยนลูกเต๋า $1$ ลูก $1$ ครั้ง คือ $S=\left\{1,\ 2,\ 3,\ 4,\ 5,\ 6\right\}$
และเหตุการณ์ที่โยนลูกเต๋า $1$ ลูก $1$ ครั้งแล้วแต้มของลูกเต๋าออกมาน้อยกว่า $3$ คือ $E=\left\{1,\ 2\right\}$
ดังนั้น ความน่าจะเป็นของการโยนลูกเต๋า $1$ ลูก $1$ ครั้งแล้วแต้มของลูกเต๋าออกมาน้อยกว่า $3$ เท่ากับ

\begin{align*} P(E) = \displaystyle\frac{2}{6} = \displaystyle\frac{1}{3} \end{align*}

บางครั้งการหาความน่าจะเป็นก็ไม่ได้ยากอย่างที่คิดนะค้าบบ เพราะน้อง ๆ สามารถเอาหลักการนับเบื้องต้นที่ได้พูดถึงมาแล้ว มาช่วยหาจำนวนวิธีที่เป็นไปได้ ตัวอย่างเช่น

Ex. จงหาความน่าจะเป็นที่จะสร้างจำนวนเต็มบวก $3$ หลักจากเลขโดด $0,1,3,5,8,9$ ที่มีค่าไม่น้อยกว่า $500$
วิธีทำ ให้ $S$ เป็นปริภูมิตัวอย่างของการสร้างจำนวนเต็มบวก $3$ หลักจากเลขโดด $0,1,3,5,8,9$
พิจารณาการหาจำนวนสมาชิกทั้งหมดของปริภูมิตัวอย่าง $S$ ดังนี้
ขั้นตอนที่ 1 เลือกเลขโดดในหลักร้อย (เลือกทุกตัวยกเว้น $0$ ) ทำได้ $5$ วิธี
ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะเลือกเลขโดดในหลักสิบได้ $6$ วิธี
ขั้นตอนที่ 3 จากขั้นตอนที่ 1 - 2 สามารถเลือกเลขโดดในหลักหน่วยได้ $6$ วิธี
โดยหลักการคูณ จะได้ว่า ปริภูมิตัวอย่าง $S$ มีสมาชิกทั้งหมด $5 \times 6 \times 6 = 180$ วิธี

ให้ $E$ เป็นเหตุการณ์ของการสร้างจำนวนเต็มบวก $3$ หลักจากเลขโดด $0,1,3,5,8,9$ ที่มีค่าไม่น้อยกว่า $500$
(นั่นคือ สร้างจำนวนที่มีค่ามากกว่าหรือเท่ากับ $500$ )
พิจารณาการหาจำนวนสมาชิกทั้งหมดของเหตุการณ์ $E$ ดังนี้
ขั้นตอนที่ 1 เลือกเลขโดดในหลักร้อย (เลือกทุกตัวยกเว้น $0$ ) ทำได้ $3$ วิธี
ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะเลือกเลขโดดในหลักสิบได้ $6$ วิธี
ขั้นตอนที่ 3 จากขั้นตอนที่ 1 - 2 สามารถเลือกเลขโดดในหลักหน่วยได้ $6$ วิธี
โดยหลักการคูณ จะได้ว่า เหตุการณ์ $E$ มีสมาชิกทั้งหมด $3 \times 6 \times 6 = 108$ วิธี

ดังนั้น ความน่าจะเป็นที่จะสร้างจำนวนเต็มบวก $3$ หลักจากเลขโดด $0,1,3,5,8,9$ ที่มีค่าไม่น้อยกว่า $500$ เท่ากับ

\begin{align*} P(E) = \displaystyle\frac{108}{180} = \displaystyle\frac{3}{5} \end{align*}

ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1 เรื่องหลักการนับเบื้องต้นและความน่าจะเป็น (ปี 64)

สำนักงานเขตแห่งหนึ่งจัดที่นั่งสำหรับผู้มารอทำบัตรประชาชน โดยเป็นเก้าอี้ $11$ ตัว ที่วางเรียงกันเป็นแถวหน้ากระดานหนึ่งแถว เพื่อเป็นการป้องกันการระบาดของโรคโควิด $-19$ จึงไม่ให้มีการนั่งเก้าอี้ติดกัน ถ้าในช่วงเวลาหนึ่งมีผู้มารอทำบัตรประชาชน $5$ คน แล้วจะมีวิธีการจัดที่นั่งให้ทั้ง $5$ คน ได้ทั้งหมดกี่วิธี

$\displaystyle\frac{11!}{6!}$
$\displaystyle\frac{11!}{5!\ 6!}$
$\displaystyle\frac{7!}{2!}$
$\displaystyle\frac{7!}{5!\ 2!}$
$5!$

วิธีทำ พิจารณาการการจัดที่นั่งสำหรับการทำบัตรประชาชน ดังนี้
ขั้นตอนที่ 1 นำเก้าอี้ $6$ ตัวมาเรียงแถวหน้ากระดาน ทำได้ $1$ วิธี

ขั้นตอนที่ 2 จากขั้นตอนที่ 1 จะเห็นว่ามีช่องว่างระหว่างเก้าอี้ทั้งหมด $7$ ช่อง โดยสามารถนำคน $5$ คนมาแทรกระหว่างช่องว่าง $7$ ที่นี้

ซึ่งทำได้ $P_{7,5}= \displaystyle\frac{7!}{(7-5)!} = \displaystyle\frac{7!}{2!}$ วิธี

ดังนั้น การจัดที่นั่งให้ทั้ง $5$ คน จะสามารถทำได้ทั้งหมด $\displaystyle\frac{7!}{2!}$ วิธี

ตอบ ข้อ 3. $\displaystyle\frac{7!}{2!}$