สวัสดีคร้าบบบ^^ วันนี้พี่หมอแม็คจะพาน้อง ๆ มาทำความรู้จักกับลำดับและอนุกรม บทนี้จะเรียกว่าเป็นบทปราบเซียนก็ว่าได้เลยครับ แต่ไม่ว่าจะยากขนาดไหนพี่แม็คก็สรุปให้น้อง ๆ ให้เข้าใจได้ง่ายมากขึ้น พร้อมตัวอย่างโจทย์ นอกจากนี้ยังมีเทคนิคเล็ก ๆ น้อย ๆ ในการทำข้อสอบมาฝากกันด้วย ถ้าพร้อมแล้ว ไปลุยกันเล้ยยย!
น้องๆ อาจจะเคยเห็นแบบรูปและความสัมพันธ์ที่เขียนในลักษณะนี้มาบ้างแล้ว
7 3 8 0 10 − 6 14 … \begin{align*} \begin{matrix} 7\ &3\ &8\ &0\ &10&-6&14&\ldots \end{matrix} \end{align*} 7 3 8 0 10 − 6 14 …
ในที่นี้จะเรียก 7 7 7 1 1 1 3 3 3 2 2 2 8 8 8 3 3 3 … \ldots … − 6 -6 − 6 6 6 6 … \ldots …
ในทางคณิตศาสตร์แล้วนั้นลำดับ (sequence) เป็นฟังก์ชันจากเซต { 1 , 2 , 3 , … , n } \{1,2,3,\ldots,n\} { 1 , 2 , 3 , … , n } N \mathbb{N} N R \mathbb{R} R
โดยลำดับที่มีโดเมนเป็นเซต { 1 , 2 , 3 , … , n } \{1,2,3,\ldots,n\} { 1 , 2 , 3 , … , n } ลำดับจำกัด (finite sequence)และเรียกลำดับที่มีโดเมนเป็น N \mathbb{N} N ลำดับอนันต์ (infinite sequence)
ปกติแล้วฟังก์ชันจะเขียนแทนค่าของฟังก์ชันด้วย f ( x ) f(x) f ( x ) f f f x x x a n a_n a n n n n
ลำดับสามารถเขียนได้หลายแบบ ดังนี้(1) การเขียนลำดับแบบแจกแจงพจน์ของลำดับ a 1 , a 2 , a 3 , … , a n , … \begin{align*} \begin{matrix} a_1, & a_2, & a_3, & \ldots, & a_n, & \ldots \end{matrix} \end{align*} a 1 , a 2 , a 3 , … , a n , … โดยที่ a 1 a_1 a 1 1 1 1 a 2 a_2 a 2 2 2 2 a 3 a_3 a 3 3 3 3 ⋮ \vdots ⋮ และ a n a_n a n n n n ⋮ \vdots ⋮
นอกจากนี้จะเรียกพจน์ที่ n n n a n a_n a n พจน์ทั่วไป (general term) ของลำดับ
Ex. กำหนดให้ลำดับ
0 , − 4 , − 8 , − 12 , − 16 , − 20 , − 24 , − 28 , − 32 \begin{align*} \begin{matrix} 0,\ & -4, & -8, & -12, & -16, & -20, & -24, & -28, & -32 \end{matrix} \end{align*} 0 , − 4 , − 8 , − 12 , − 16 , − 20 , − 24 , − 28 , − 32
ลำดับนี้เป็นลำดับจำกัด ซึ่งมีพจน์ที่ 1 1 1 0 0 0 2 2 2 − 4 -4 − 4 3 3 3 − 8 -8 − 8 … \ldots … 9 9 9 − 32 -32 − 32
(2) การเขียนลำดับโดยเขียนพจน์ทั่วไปของลำดับ
Ex. กำหนดให้ลำดับ a n = 3 6 − n a_n=3^{6-n} a n = 3 6 − n n ∈ { 1 , 2 , 3 , … , 10 } n\in\{1,2,3,\ldots,10\} n ∈ { 1 , 2 , 3 , … , 10 }
ลำดับนี้เป็นลำดับจำกัด ซึ่งมีพจน์ที่ 1 1 1 a 1 = 3 6 − 1 = 3 5 = 243 a_1=3^{6-1}=3^5=243 a 1 = 3 6 − 1 = 3 5 = 243 พจน์ที่ 2 2 2 a 2 = 3 6 − 2 = 3 4 = 81 a_2=3^{6-2}=3^4=81 a 2 = 3 6 − 2 = 3 4 = 81 พจน์ที่ 3 3 3 a 3 = 3 6 − 3 = 3 3 = 27 a_3=3^{6-3}=3^3=27 a 3 = 3 6 − 3 = 3 3 = 27 ⋮ \vdots ⋮ พจน์ที่ 10 10 10 a 10 = 3 6 − 10 = 3 − 4 = 1 81 a_{10}=3^{6-10}=3^{-4}=\displaystyle\frac{1}{81} a 10 = 3 6 − 10 = 3 − 4 = 81 1
Ex. กำหนดให้ลำดับ a n = 2 n + 1 a_n=2^{n}+1 a n = 2 n + 1 n ∈ N n\in\mathbb{N} n ∈ N
ลำดับนี้เป็นลำดับอนันต์ ซึ่งมีพจน์ที่ 1 1 1 a 1 = 2 1 + 1 = 2 + 1 = 2 a_1=2^{1}+1=2+1=2 a 1 = 2 1 + 1 = 2 + 1 = 2 พจน์ที่ 2 2 2 a 2 = 2 2 + 1 = 4 + 1 = 5 a_2=2^{2}+1=4+1=5 a 2 = 2 2 + 1 = 4 + 1 = 5 พจน์ที่ 3 3 3 a 3 = 2 3 + 1 = 8 + 1 = 9 a_3=2^{3}+1=8+1=9 a 3 = 2 3 + 1 = 8 + 1 = 9 ⋮ \vdots ⋮
โดยปกติแล้ว ผลต่างร่วมของลำดับเลขคณิต จะเขียนแทนด้วย d = a n + 1 − a n d = a_{n+1}-a_n d = a n + 1 − a n ให้ a 1 a_1 a 1 1 1 1 d d d จะได้ว่า พจน์ที่ 2 2 2 a 2 = a 1 + d a_2=a_1+d a 2 = a 1 + d พจน์ที่ 3 3 3 a 3 = a 2 + d = a 1 + 2 d a_3=a_2+d=a_1+2d a 3 = a 2 + d = a 1 + 2 d พจน์ที่ 4 4 4 a 4 = a 3 + d = a 1 + 3 d a_4=a_3+d=a_1+3d a 4 = a 3 + d = a 1 + 3 d ⋮ \vdots ⋮ ดังนั้น ลำดับเลขคณิต มีพจน์ทั่วไปเป็น a n = a 1 + ( n − 1 ) d a_n=a_1+(n-1)d a n = a 1 + ( n − 1 ) d
Ex. จงหาพจน์ที่ 20 20 20 7 , 12 , 17 , 22 , … 7, 12, 17, 22, \dots 7 , 12 , 17 , 22 , … วิธีทำ หาผลต่างร่วมของลำดับเลขคณิต จะได้ว่า d = 12 − 7 = 5 d=12-7=5 d = 12 − 7 = 5 ต่อไปจะหาพจน์ที่ 20 20 20 a n = a 1 + ( n − 1 ) d a_n = a_1+(n-1)d a n = a 1 + ( n − 1 ) d
a 20 = a 1 + ( 20 − 1 ) 5 = 7 + ( 19 ) 5 = 7 + 95 = 102 \begin{align*} a_{20} &= a_1+(20-1)5\\ &= 7+(19)5\\ &= 7+95\\ &= 102 \end{align*} a 20 = a 1 + ( 20 − 1 ) 5 = 7 + ( 19 ) 5 = 7 + 95 = 102
Ex. กำหนดให้ลำดับเลขคณิต 3 , 10 , 17 , 24 , … 3, 10, 17, 24, \ldots 3 , 10 , 17 , 24 , … 346 346 346 วิธีทำ หาผลต่างร่วมของลำดับเลขคณิต จะได้ว่า d = 24 − 17 = 7 d=24-17=7 d = 24 − 17 = 7 ให้ a n = 346 a_n = 346 a n = 346 a n = a 1 + ( n − 1 ) d a_n = a_1+(n-1)d a n = a 1 + ( n − 1 ) d
346 = 3 + ( n − 1 ) 7 343 = 7 ( n − 1 ) n − 1 = 343 7 n − 1 = 49 n = 50 \begin{align*} 346 &= 3+(n-1)7\\ 343 &= 7(n-1)\\ n-1&= \frac{343}{7}\\ n-1&= 49\\ n &= 50 \end{align*} 346 343 n − 1 n − 1 n = 3 + ( n − 1 ) 7 = 7 ( n − 1 ) = 7 343 = 49 = 50
โดยปกติแล้ว อัตราส่วนร่วมของลำดับเรขาคณิต จะเขียนแทนด้วย r = a n + 1 a n r = \displaystyle\frac{a_{n+1}}{a_n} r = a n a n + 1 ให้ a 1 a_1 a 1 1 1 1 r r r จะได้ว่า พจน์ที่ 2 2 2 a 2 = a 1 r a_2=a_1r a 2 = a 1 r พจน์ที่ 3 3 3 a 3 = a 2 r = a 1 r 2 a_3=a_2r=a_1r^2 a 3 = a 2 r = a 1 r 2 พจน์ที่ 4 4 4 a 4 = a 3 r = a 1 r 3 a_4=a_3r=a_1r^3 a 4 = a 3 r = a 1 r 3 ⋮ \vdots ⋮ ดังนั้น ลำดับเรขาคณิต มีพจน์ทั่วไปเป็น a n = a 1 r n − 1 a_n=a_1r^{n-1} a n = a 1 r n − 1
Ex. จงหาพจน์ทั่วไปของลำดับเรขาคณิต 2 , − 6 , 18 , − 54 , … 2, -6, 18, -54, \dots 2 , − 6 , 18 , − 54 , … วิธีทำ เนื่องจากอัตราส่วนร่วมของลำดับเรขาคณิต คือ r = a n + 1 a n = − 6 2 = − 3 r = \displaystyle\frac{a_{n+1}}{a_n} = \displaystyle\frac{-6}{2} = -3 r = a n a n + 1 = 2 − 6 = − 3 a 1 = 2 a_1 = 2 a 1 = 2 พจน์ทั่วไปของลำดับเรขาคณิต 2 , − 6 , 18 , − 54 , … 2, -6, 18, -54, \dots 2 , − 6 , 18 , − 54 , … a n = 2 ( − 3 ) n − 1 a_n=2(-3)^{n-1} a n = 2 ( − 3 ) n − 1
Ex. ลำดับเรขาคณิตชุดหนึ่งมีพจน์ที่ 3 3 3 12 12 12 6 6 6 96 96 96 10 10 10 วิธีทำ เนื่องจากลำดับเรขาคณิตชุดหนึ่งมีพจน์ที่ 3 3 3 12 12 12 a 3 = a 1 r 2 = 12 a_3=a_1r^2 = 12 a 3 = a 1 r 2 = 12 และพจน์ที่ 6 6 6 96 96 96 a 6 = a 1 r 5 = 96 a_6=a_1r^5 = 96 a 6 = a 1 r 5 = 96 ดังนั้น a 6 a 3 = a 1 r 5 a 1 r 2 = r 3 \displaystyle\frac{a_6}{a_3} = \displaystyle\frac{a_1r^5}{a_1r^2} = r^3 a 3 a 6 = a 1 r 2 a 1 r 5 = r 3 a 6 a 3 = 96 12 = 8 \displaystyle\frac{a_6}{a_3} = \displaystyle\frac{96}{12} = 8 a 3 a 6 = 12 96 = 8 ทำให้ได้ว่า r = 2 r=2 r = 2 a 1 = a 3 r 2 = 12 4 = 3 a_1 = \displaystyle\frac{a_3}{r^2}= \displaystyle\frac{12}{4} = 3 a 1 = r 2 a 3 = 4 12 = 3 เพราะฉะนั้น ลำดับเรขาคณิต มีพจน์ทั่วไปเป็น a n = a 1 r n − 1 = 3 ⋅ 2 n − 1 a_n=a_1r^{n-1} = 3 \cdot 2^{n-1} a n = a 1 r n − 1 = 3 ⋅ 2 n − 1 ดังนั้น พจน์ที่ 10 10 10 a 10 = 3 ⋅ 2 10 − 1 = 3 ( 512 ) = 1536 a_{10}=3 \cdot 2^{10-1} = 3(512) = 1536 a 10 = 3 ⋅ 2 10 − 1 = 3 ( 512 ) = 1536
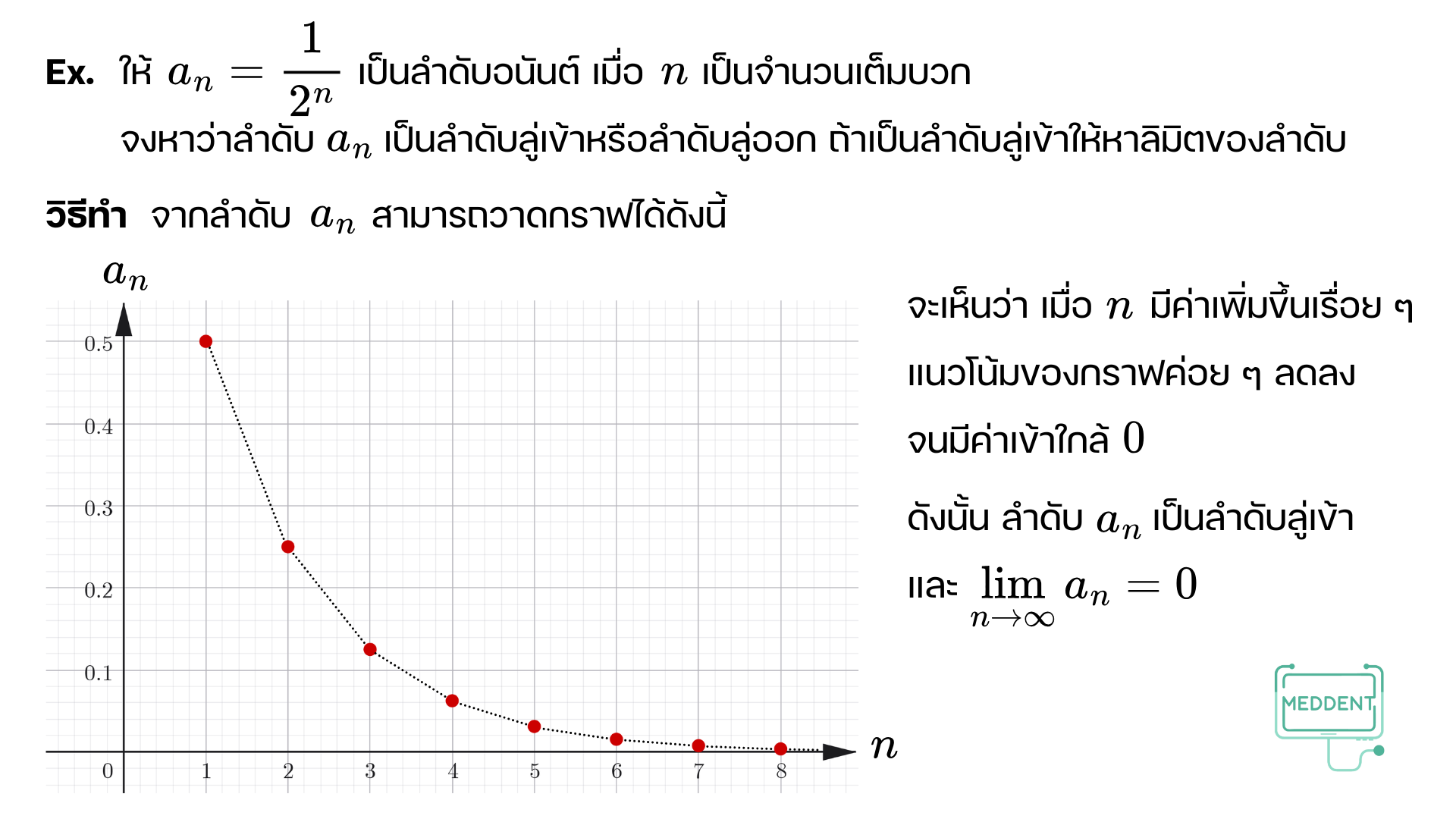
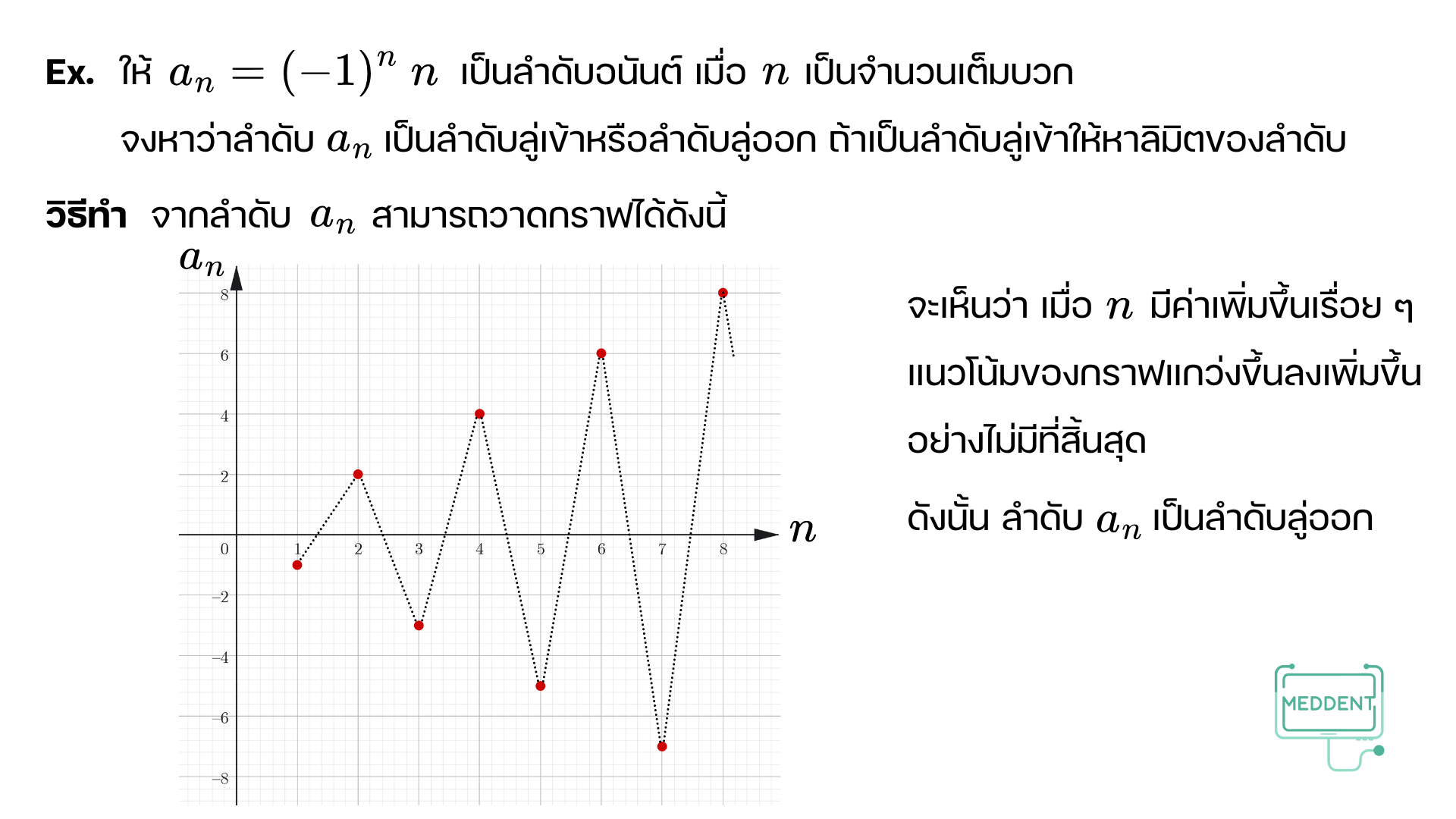
ลำดับอนันต์เป็นลำดับที่มีโดเมนเป็น N \mathbb{N} N n n n n n n a 1 , a 2 , a 3 , … , a n , … a_1, a_2, a_3, \ldots, a_n, \ldots a 1 , a 2 , a 3 , … , a n , …
การพิจารณาพจน์ที่ n n n n n n
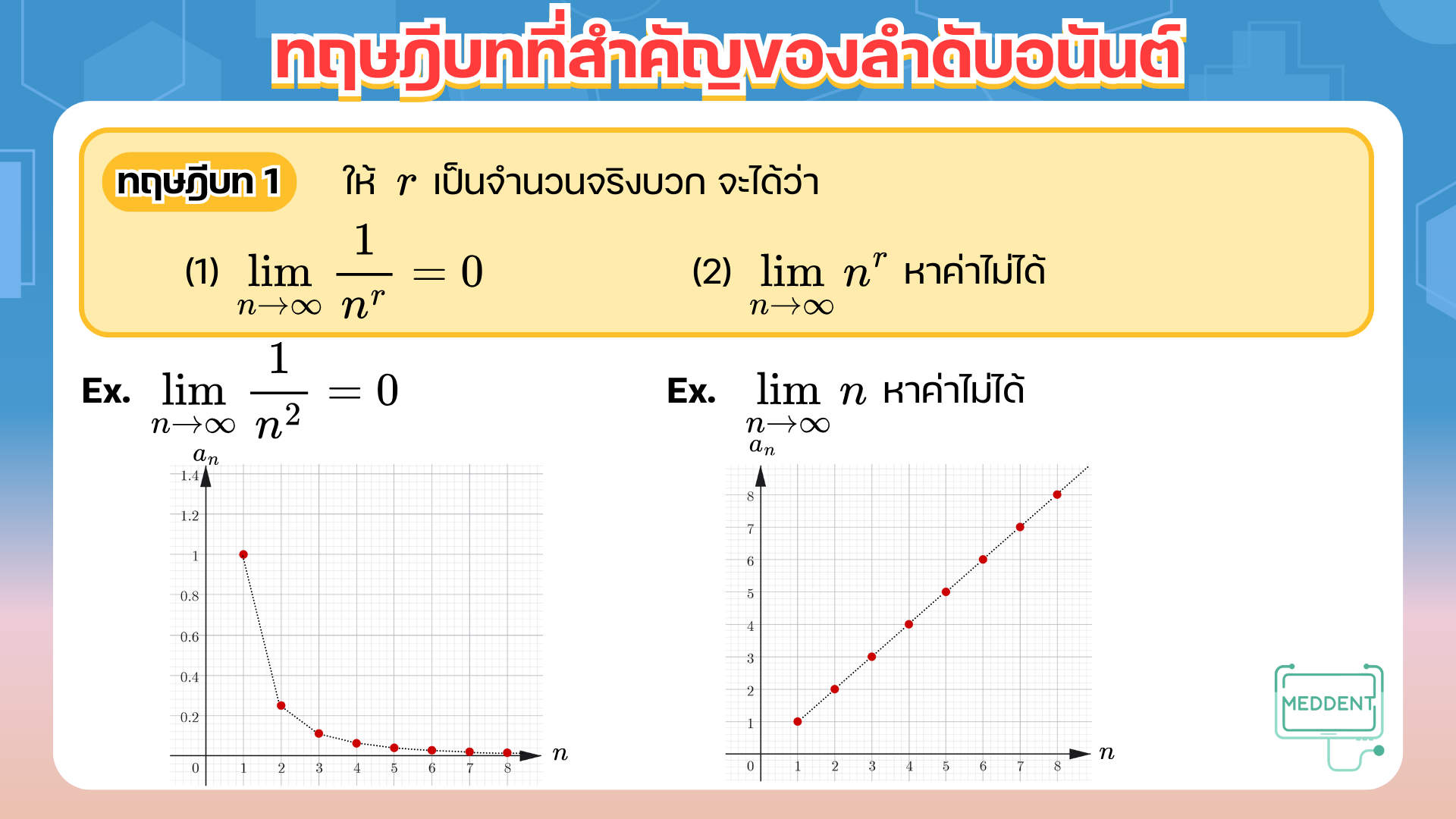
ทฤษฎีบท 1 ให้ r r r lim n → ∞ 1 n r = 0 \displaystyle\lim_{n\to\infty} \frac{1}{n^r} = 0 n → ∞ lim n r 1 = 0 lim n → ∞ n r \displaystyle\lim_{n\to\infty} n^r n → ∞ lim n r
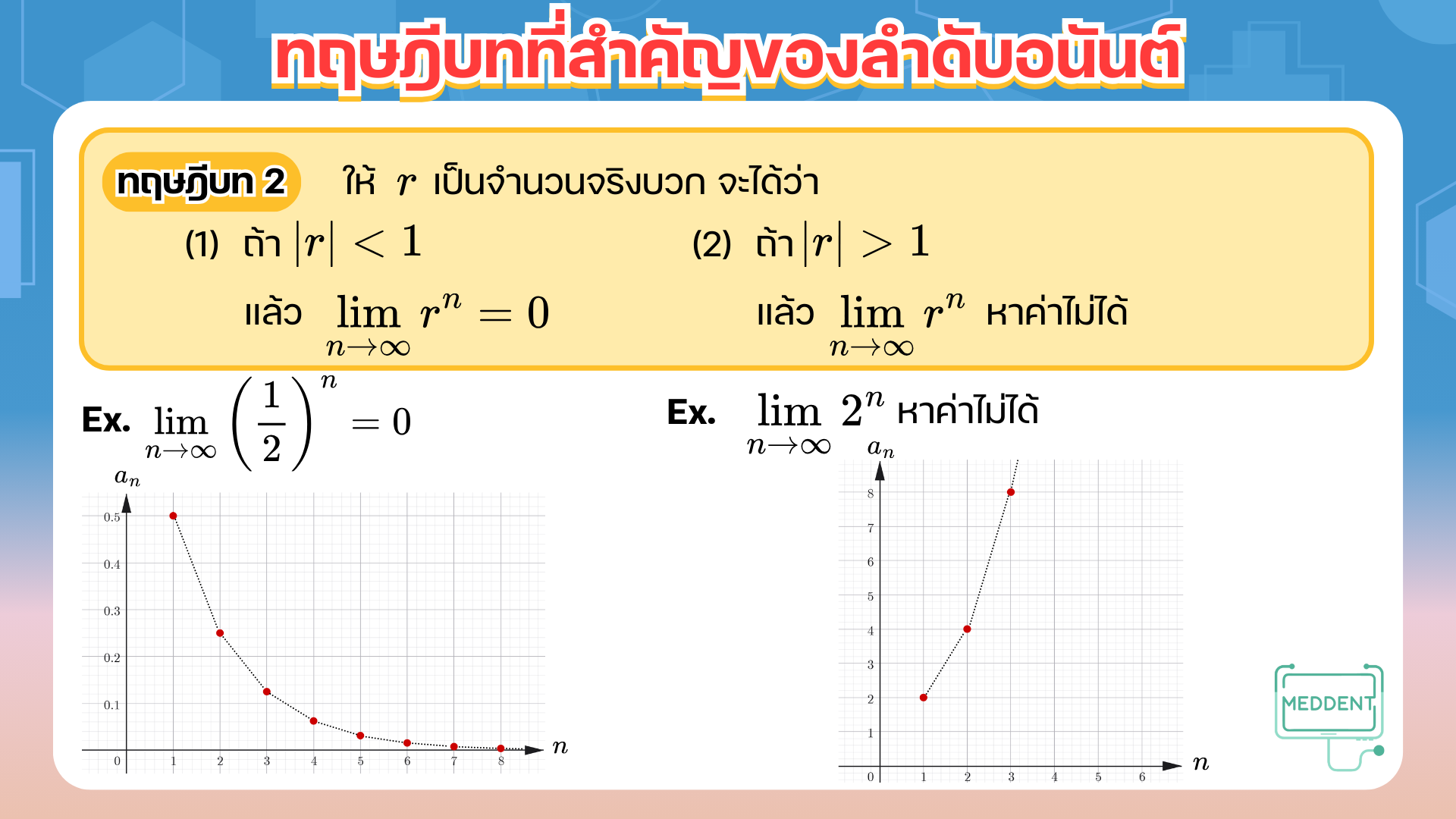
ทฤษฎีบท 2 ให้ r r r (1) ถ้า ∣ r ∣ < 1 \left| r \right| < 1 ∣ r ∣ < 1 lim n → ∞ r n = 0 \displaystyle\lim_{n\to\infty} r^n = 0 n → ∞ lim r n = 0 (2) ถ้า ∣ r ∣ > 1 \left| r \right| > 1 ∣ r ∣ > 1 lim n → ∞ r n \displaystyle\lim_{n\to\infty} r^n n → ∞ lim r n
ทฤษฎีบท 3 ให้ a n , b n a_n, b_n a n , b n A , B A, B A , B c c c โดยที่ lim n → ∞ a n = A \displaystyle\lim_{n \to \infty} a_n = A n → ∞ lim a n = A lim n → ∞ b n = B \displaystyle\lim_{n \to \infty} b_n = B n → ∞ lim b n = B
ถ้า t n = c t_n = c t n = c n n n lim n → ∞ t n = lim n → ∞ c = c \displaystyle\lim_{n \to \infty} t_n = \lim_{n \to \infty} c = c n → ∞ lim t n = n → ∞ lim c = c lim n → ∞ c a n = c lim n → ∞ a n = c A \displaystyle\lim_{n \to \infty} c a_n = c \lim_{n \to \infty} a_n = cA n → ∞ lim c a n = c n → ∞ lim a n = c A lim n → ∞ ( a n + b n ) = lim n → ∞ a n + lim n → ∞ b n = A + B \displaystyle\lim_{n \to \infty} (a_n + b_n) = \lim_{n \to \infty} a_n + \lim_{n \to \infty} b_n = A + B n → ∞ lim ( a n + b n ) = n → ∞ lim a n + n → ∞ lim b n = A + B lim n → ∞ ( a n − b n ) = lim n → ∞ a n − lim n → ∞ b n = A − B \displaystyle\lim_{n \to \infty} (a_n - b_n) = \lim_{n \to \infty} a_n - \lim_{n \to \infty} b_n = A - B n → ∞ lim ( a n − b n ) = n → ∞ lim a n − n → ∞ lim b n = A − B lim n → ∞ ( a n ⋅ b n ) = lim n → ∞ a n ⋅ lim n → ∞ b n = A B \displaystyle\lim_{n \to \infty} (a_n \cdot b_n) = \lim_{n \to \infty} a_n \cdot \lim_{n \to \infty} b_n = AB n → ∞ lim ( a n ⋅ b n ) = n → ∞ lim a n ⋅ n → ∞ lim b n = A B ถ้า b n ≠ 0 b_n \neq 0 b n = 0 n n n B ≠ 0 B \neq 0 B = 0 lim n → ∞ ( a n b n ) = lim n → ∞ a n lim n → ∞ b n = A B \displaystyle\lim_{n \to \infty} \left( \displaystyle\frac{a_n}{b_n} \right) = \displaystyle\frac{\displaystyle\lim_{n \to \infty} a_n}{\displaystyle\lim_{n \to \infty} b_n} = \displaystyle\frac{A}{B} n → ∞ lim ( b n a n ) = n → ∞ lim b n n → ∞ lim a n = B A Ex. จงหาค่าของลิมิตของลำดับ a n a_n a n a n = 3 n 2 − 1 \displaystyle a_n = \frac{3}{n^2}-1 a n = n 2 3 − 1 วิธีทำ ในการหาค่าของ lim n → ∞ a n = lim n → ∞ ( 3 n 2 − 1 ) \displaystyle \lim_{n \to \infty} a_n = \lim_{n \to \infty} \left( \frac{3}{n^2}-1 \right) n → ∞ lim a n = n → ∞ lim ( n 2 3 − 1 )
lim n → ∞ a n = lim n → ∞ ( 3 n 2 − 1 ) = lim n → ∞ ( 3 ⋅ 1 n 2 − 1 ) = ( lim n → ∞ 3 ⋅ lim n → ∞ 1 n 2 ) − lim n → ∞ 1 = ( 3 ⋅ 0 ) − 1 = − 1 \begin{align*} \displaystyle \lim_{n \to \infty} a_n &= \displaystyle \lim_{n \to \infty} \left( \displaystyle\frac{3}{n^2}-1 \right) \\ &= \displaystyle \lim_{n \to \infty} \left( 3 \cdot \displaystyle\frac{1}{n^2}-1 \right) \\ &= \displaystyle \left( \lim_{n \to \infty} 3 \cdot \lim_{n \to \infty}\displaystyle\frac{1}{n^2} \right)-\lim_{n \to \infty}1 \\ &= (3 \cdot 0)-1 \\ &= -1 \end{align*} n → ∞ lim a n = n → ∞ lim ( n 2 3 − 1 ) = n → ∞ lim ( 3 ⋅ n 2 1 − 1 ) = ( n → ∞ lim 3 ⋅ n → ∞ lim n 2 1 ) − n → ∞ lim 1 = ( 3 ⋅ 0 ) − 1 = − 1
Ex. จงหาค่าของลิมิตของลำดับ a n a_n a n a n = 3 n + 5 n − 1 \displaystyle a_n = \frac{3n + 5}{n - 1} a n = n − 1 3 n + 5 วิธีทำ ในการหาค่าของ lim n → ∞ a n = lim n → ∞ ( 3 n + 5 n − 1 ) \displaystyle \lim_{n \to \infty} a_n = \displaystyle \lim_{n \to \infty} \left( \displaystyle\frac{3n + 5}{n - 1} \right) n → ∞ lim a n = n → ∞ lim ( n − 1 3 n + 5 )
หารด้วย n n n lim n → ∞ a n = lim n → ∞ ( 3 n + 5 n n − 1 n ) = lim n → ∞ ( 3 n n + 5 n n n − 1 n ) = lim n → ∞ ( 3 + 5 n 1 − 1 n ) \begin{align*} \displaystyle \lim_{n \to \infty} a_n &= \displaystyle \lim_{n \to \infty} \left(\displaystyle\frac{\displaystyle\frac{3n + 5}{n}}{\displaystyle\frac{n - 1}{n}} \right) \\ &= \displaystyle \lim_{n \to \infty} \left( \displaystyle\frac{\displaystyle\frac{3n}{n}+\displaystyle\frac{5}{n}}{\displaystyle\frac{n}{n}-\displaystyle\frac{1}{n}} \right) \\ &= \displaystyle \lim_{n \to \infty} \left( \displaystyle\frac{3+\displaystyle\frac{5}{n}}{1-\displaystyle\frac{1}{n}} \right) \end{align*} n → ∞ lim a n = n → ∞ lim n n − 1 n 3 n + 5 = n → ∞ lim n n − n 1 n 3 n + n 5 = n → ∞ lim 1 − n 1 3 + n 5 โดยทฤษฎีบท 1 (ข้อ 1) lim n → ∞ 1 n r = 0 \displaystyle\lim_{n\to\infty} \frac{1}{n^r} = 0 n → ∞ lim n r 1 = 0 lim n → ∞ a n = lim n → ∞ 3 + lim n → ∞ 5 n lim n → ∞ 1 − lim n → ∞ 1 n = 3 + 0 1 − 0 = 3 \begin{align*} \displaystyle \lim_{n \to \infty} a_n &= \displaystyle\frac{\displaystyle \lim_{n \to \infty}3+\displaystyle \lim_{n \to \infty}\displaystyle\frac{5}{n}}{\displaystyle \lim_{n \to \infty}1-\displaystyle \lim_{n \to \infty}\displaystyle\frac{1}{n}} \\ &= \displaystyle\frac{3+0}{1-0} \\ &= 3 \end{align*} n → ∞ lim a n = n → ∞ lim 1 − n → ∞ lim n 1 n → ∞ lim 3 + n → ∞ lim n 5 = 1 − 0 3 + 0 = 3 ถ้า a 1 , a 2 , a 3 , … , a n a_1, a_2, a_3, \ldots, a_n a 1 , a 2 , a 3 , … , a n n n n การเขียนแสดงการบวกของพจน์ที่ 1 1 1 n n n a 1 + a 2 + a 3 + ⋯ + a n a_1+a_2+a_3+\cdots+a_n a 1 + a 2 + a 3 + ⋯ + a n อนุกรมจำกัด (finite series)
ถ้า a 1 , a 2 , a 3 , … , a n a_1, a_2, a_3, \ldots, a_n a 1 , a 2 , a 3 , … , a n n n n d d d ให้ S n S_n S n n n n
S n = a 1 + a 2 + a 3 + ⋯ + a n = a 1 + ( a 1 + d ) + ( a 1 + 2 d ) + ⋯ + ( a 1 + ( n − 1 ) d ) \begin{align} S_n &= a_1+a_2+a_3+\cdots+a_n \notag \\ &= a_1+(a_1+d)+(a_1+2d)+\cdots+(a_1+(n-1)d) \end{align} S n = a 1 + a 2 + a 3 + ⋯ + a n = a 1 + ( a 1 + d ) + ( a 1 + 2 d ) + ⋯ + ( a 1 + ( n − 1 ) d )
และ
S n = a n + a n − 1 + a n − 2 + ⋯ + a 1 = a n + ( a n − d ) + ( a n − 2 d ) + ⋯ + ( a n − ( n − 1 ) d ) \begin{align} S_n &= a_n+a_{n-1}+a_{n-2}+\cdots+a_1 \notag \\ &= a_n+(a_n-d)+(a_n-2d)+\cdots+(a_n-(n-1)d) \end{align} S n = a n + a n − 1 + a n − 2 + ⋯ + a 1 = a n + ( a n − d ) + ( a n − 2 d ) + ⋯ + ( a n − ( n − 1 ) d )
นำสมการ (1) บวกกับสมการ (2) จะได้
2 S n = ( a 1 + a n ) + ( a 1 + a n ) + ( a 1 + a n ) + ⋯ + ( a 1 + a n ) ⏟ n วงเล็บ = n ( a 1 + a n ) \begin{align*} 2S_n &= \underbrace{(a_1+a_n)+(a_1+a_n)+(a_1+a_n)+\cdots+(a_1+a_n)}_{n \text{ วงเล็บ}} \\ &= n(a_1+a_n) \end{align*} 2 S n = n วงเล็บ ( a 1 + a n ) + ( a 1 + a n ) + ( a 1 + a n ) + ⋯ + ( a 1 + a n ) = n ( a 1 + a n )
ดังนั้น S n = n 2 ( a 1 + a n ) S_n = \displaystyle\frac{n}{2}(a_1+a_n) S n = 2 n ( a 1 + a n ) และจาก a n = a 1 + ( n − 1 ) d a_n=a_1+(n-1)d a n = a 1 + ( n − 1 ) d S n = n 2 ( 2 a 1 + ( n − 1 ) d ) S_n = \displaystyle\frac{n}{2}(2a_1+(n-1)d) S n = 2 n ( 2 a 1 + ( n − 1 ) d )
สรุปสูตรอนุกรมเลขคณิต (1) S n = n 2 ( a 1 + a n ) S_n = \displaystyle\frac{n}{2}(a_1+a_n) S n = 2 n ( a 1 + a n ) (2) S n = n 2 ( 2 a 1 + ( n − 1 ) d ) S_n = \displaystyle\frac{n}{2}(2a_1+(n-1)d) S n = 2 n ( 2 a 1 + ( n − 1 ) d )
Ex. จงหาอนุกรมเลขคณิต 5 + 9 + 13 + 17 + ⋯ + 81 5+9+13+17+\cdots+81 5 + 9 + 13 + 17 + ⋯ + 81 วิธีทำ จากอนุกรมเลขคณิต 5 + 9 + 13 + 17 + ⋯ + 81 5+9+13+17+\cdots+81 5 + 9 + 13 + 17 + ⋯ + 81 5 , 9 , 13 , 17 , … , 81 5, 9, 13,17, \ldots, 81 5 , 9 , 13 , 17 , … , 81
a n = a 1 + ( n − 1 ) d 81 = 5 + ( n − 1 ) 4 4 ( n − 1 ) = 76 n − 1 = 19 n = 20 \begin{align*} a_n &= a_1+(n-1)d \\ 81 &= 5+(n-1)4 \\ 4(n-1)&= 76 \\ n-1 &= 19 \\ n &= 20 \end{align*} a n 81 4 ( n − 1 ) n − 1 n = a 1 + ( n − 1 ) d = 5 + ( n − 1 ) 4 = 76 = 19 = 20
ต่อไปจะหาอนุกรมเลขคณิต 5 + 9 + 13 + 17 + ⋯ + 81 5+9+13+17+\cdots+81 5 + 9 + 13 + 17 + ⋯ + 81 จะได้ว่า S n = n 2 ( a 1 + a n ) = 20 2 ( a 1 + a 20 ) = 10 ( 5 + 81 ) = 10 ( 86 ) = 860 S_n = \displaystyle\frac{n}{2}(a_1+a_n) = \displaystyle\frac{20}{2}(a_1+a_{20}) = 10(5+81) = 10(86) = 860 S n = 2 n ( a 1 + a n ) = 2 20 ( a 1 + a 20 ) = 10 ( 5 + 81 ) = 10 ( 86 ) = 860
ถ้า a 1 , a 2 , a 3 , … , a n a_1, a_2, a_3, \ldots, a_n a 1 , a 2 , a 3 , … , a n n n n r r r ให้ S n S_n S n n n n
S n = a 1 + a 2 + a 3 + ⋯ + a n = a 1 + ( a 1 r ) + ( a 1 r 2 ) + ⋯ + ( a 1 r n − 1 ) \begin{align} S_n &= a_1+a_2+a_3+\cdots+a_n \notag \\ &= a_1+(a_1r)+(a_1r^2)+\cdots+(a_1r^{n-1}) \end{align} S n = a 1 + a 2 + a 3 + ⋯ + a n = a 1 + ( a 1 r ) + ( a 1 r 2 ) + ⋯ + ( a 1 r n − 1 )
และ
r S n = r a 1 + r a 2 + r a 3 + ⋯ + r a n = ( a 1 r ) + ( a 1 r 2 ) + ( a 1 r 3 ) + ⋯ + ( a 1 r n ) \begin{align} rS_n &= ra_1+ra_2+ra_3+\cdots+ra_n \notag \\ &= (a_1r)+(a_1r^2)+(a_1r^3)+\cdots+(a_1r^n) \end{align} r S n = r a 1 + r a 2 + r a 3 + ⋯ + r a n = ( a 1 r ) + ( a 1 r 2 ) + ( a 1 r 3 ) + ⋯ + ( a 1 r n )
นำสมการ (4) ลบกับสมการ (3) จะได้
r S n − S n = a 1 r n − a 1 S n ( r − 1 ) = a 1 ( r n − 1 ) S n = a 1 ( r n − 1 ) ( r − 1 ) S n = a 1 ( 1 − r n ) ( 1 − r ) \begin{align*} rS_n-S_n &= a_1r^n-a_1 \\ S_n (r-1) &= a_1(r^n-1) \\ S_n &= \displaystyle\frac{a_1(r^n-1)}{(r-1)} \\ S_n &= \displaystyle\frac{a_1(1-r^n)}{(1-r)} \end{align*} r S n − S n S n ( r − 1 ) S n S n = a 1 r n − a 1 = a 1 ( r n − 1 ) = ( r − 1 ) a 1 ( r n − 1 ) = ( 1 − r ) a 1 ( 1 − r n )
ดังนั้น S n = a 1 ( r n − 1 ) ( r − 1 ) S_n = \displaystyle\frac{a_1(r^n-1)}{(r-1)} S n = ( r − 1 ) a 1 ( r n − 1 ) S n = a 1 ( 1 − r n ) ( 1 − r ) S_n = \displaystyle\frac{a_1(1-r^n)}{(1-r)} S n = ( 1 − r ) a 1 ( 1 − r n )
สรุปสูตรอนุกรมเรขาคณิต (1) S n = a 1 ( r n − 1 ) ( r − 1 ) S_n = \displaystyle\frac{a_1(r^n-1)}{(r-1)} S n = ( r − 1 ) a 1 ( r n − 1 ) ∣ r ∣ > 1 \left|r\right|>1 ∣ r ∣ > 1 (2) S n = a 1 ( 1 − r n ) ( 1 − r ) S_n = \displaystyle\frac{a_1(1-r^n)}{(1-r)} S n = ( 1 − r ) a 1 ( 1 − r n ) ∣ r ∣ < 1 \left|r\right|<1 ∣ r ∣ < 1
Ex. จงหาผลบวกของ 6 6 6 2 , 6 , 18 , 54 , … 2, 6, 18, 54, \ldots 2 , 6 , 18 , 54 , … วิธีทำ เนื่องจากลำดับเรขาคณิต 2 , 6 , 18 , 54 , … 2, 6, 18, 54, \ldots 2 , 6 , 18 , 54 , … 1 1 1 a 1 = 2 a_1 = 2 a 1 = 2 r = 6 2 = 3 r=\displaystyle\frac{6}{2}=3 r = 2 6 = 3 และต่อไปจะหาผลบวก 6 6 6 n = 6 n=6 n = 6 จาก S n = a 1 ( r n − 1 ) ( r − 1 ) S_n = \displaystyle\frac{a_1(r^n-1)}{(r-1)} S n = ( r − 1 ) a 1 ( r n − 1 ) S 6 = 2 ( 3 6 − 1 ) ( 3 − 1 ) = 2 ( 729 − 1 ) 2 = 728 S_6 = \displaystyle\frac{2(3^6-1)}{(3-1)} = \displaystyle\frac{2(729-1)}{2} = 728 S 6 = ( 3 − 1 ) 2 ( 3 6 − 1 ) = 2 2 ( 729 − 1 ) = 728
Ex. จงหาผลบวกของ 8 พจน์แรกของลำดับเรขาคณิต 256 , 128 , 64 , 32 , … 256, 128, 64, 32, \dots 256 , 128 , 64 , 32 , … วิธีทำ เนื่องจากลำดับเรขาคณิต 256 , 128 , 64 , 32 , … 256, 128, 64, 32, \dots 256 , 128 , 64 , 32 , … 1 1 1 a 1 = 256 a_1 = 256 a 1 = 256 r = 128 256 = 1 2 r=\displaystyle\frac{128}{256}=\displaystyle\frac{1}{2} r = 256 128 = 2 1 และต่อไปจะหาผลบวก 8 8 8 n = 8 n=8 n = 8 จาก S n = a 1 ( 1 − r n ) ( 1 − r ) S_n = \displaystyle\frac{a_1(1-r^n)}{(1-r)} S n = ( 1 − r ) a 1 ( 1 − r n ) จะได้ว่า S 8 = 256 ( 1 − ( 1 2 ) 8 ) 1 − 1 2 = 256 ( 1 − 1 256 ) 1 2 = 2 ⋅ 256 ( 256 − 1 256 ) = 2 ⋅ 255 = 510 S_8 = \displaystyle\frac{256\left(1-\left(\displaystyle\frac{1}{2}\right)^8\right)}{1-\displaystyle\frac{1}{2}} = \displaystyle\frac{256\left(1-\displaystyle\frac{1}{256}\right)}{\displaystyle\frac{1}{2}} = 2 \cdot 256\left(\displaystyle\frac{256-1}{256}\right) = 2 \cdot 255 = 510 S 8 = 1 − 2 1 256 ( 1 − ( 2 1 ) 8 ) = 2 1 256 ( 1 − 256 1 ) = 2 ⋅ 256 ( 256 256 − 1 ) = 2 ⋅ 255 = 510
ถ้า a 1 , a 2 , a 3 , … , a n , … a_1, a_2, a_3, \ldots, a_n, \ldots a 1 , a 2 , a 3 , … , a n , … การเขียนแสดงการบวกที่เขียนอยู่ในรูป a 1 + a 2 + a 3 + ⋯ + a n + ⋯ a_1+a_2+a_3+\cdots+a_n+\cdots a 1 + a 2 + a 3 + ⋯ + a n + ⋯ อนุกรมอนันต์ (infinite series)
กำหนดให้
S 1 = a 1 S 2 = a 1 + a 2 S 3 = a 1 + a 2 + a 3 ⋮ S n = a 1 + a 2 + a 3 + ⋯ + a n \begin{align*} S_1 &= a_1 \\ S_2 &= a_1 + a_2 \\ S_3 &= a_1 + a_2 + a_3 \\ &\vdots \\ S_n &= a_1+a_2+a_3+\cdots+a_n \end{align*} S 1 S 2 S 3 S n = a 1 = a 1 + a 2 = a 1 + a 2 + a 3 ⋮ = a 1 + a 2 + a 3 + ⋯ + a n
เรียก S n S_n S n ผลบวกย่อย (partial sum) n n n และเรียก S 1 , S 2 , S 3 , … , S n S_1,S_2,S_3, \ldots, S_n S 1 , S 2 , S 3 , … , S n ลำดับของผลบวกย่อยของอนุกรม
ถ้าลำดับ S n S_n S n lim n → ∞ S n = S \displaystyle\lim_{n\to\infty} S_n = S n → ∞ lim S n = S แล้วอนุกรม a 1 + a 2 + a 3 + ⋯ + a n + ⋯ a_1+a_2+a_3+\cdots+a_n+\cdots a 1 + a 2 + a 3 + ⋯ + a n + ⋯ อนุกรมลู่เข้า (convergent series)
ถ้าลำดับ S n S_n S n แล้วอนุกรม a 1 + a 2 + a 3 + ⋯ + a n + ⋯ a_1+a_2+a_3+\cdots+a_n+\cdots a 1 + a 2 + a 3 + ⋯ + a n + ⋯ อนุกรมลู่ออก (divergent series)
Ex. จงหาลำดับของผลบวกย่อย 3 4 + 9 16 + 27 64 + ⋯ + ( 3 4 ) n + ⋯ \displaystyle \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots + \left(\frac{3}{4}\right)^n + \cdots 4 3 + 16 9 + 64 27 + ⋯ + ( 4 3 ) n + ⋯ วิธีทำ เนื่องจากอนุกรม 3 4 + 9 16 + 27 64 + ⋯ + ( 3 4 ) n + ⋯ \displaystyle \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots + \left(\frac{3}{4}\right)^n + \cdots 4 3 + 16 9 + 64 27 + ⋯ + ( 4 3 ) n + ⋯ มีพจน์ที่ 1 1 1 a 1 = 3 4 a_1 = \displaystyle \frac{3}{4} a 1 = 4 3 r = 9 16 3 4 = 3 4 r=\displaystyle\frac{\displaystyle \frac{9}{16}}{\displaystyle \frac{3}{4}}=\displaystyle \frac{3}{4} r = 4 3 16 9 = 4 3 n n n จาก S n = a 1 ( 1 − r n ) ( 1 − r ) S_n = \displaystyle\frac{a_1(1-r^n)}{(1-r)} S n = ( 1 − r ) a 1 ( 1 − r n ) จะได้ว่า S n = 3 4 ( 1 − ( 3 4 ) n ) 1 − 3 4 = 3 4 ( 1 − ( 3 4 ) n ) 1 4 = 3 ( 1 − ( 3 4 ) n ) S_n = \displaystyle\frac{\displaystyle \frac{3}{4} \left(1-\left(\displaystyle \frac{3}{4}\right)^n\right)}{1-\displaystyle \frac{3}{4}} = \displaystyle\frac{\displaystyle \frac{3}{4} \left(1-\left(\displaystyle \frac{3}{4}\right)^n\right)}{\displaystyle \frac{1}{4}} = 3 \left(1-\left(\displaystyle \frac{3}{4}\right)^n\right) S n = 1 − 4 3 4 3 ( 1 − ( 4 3 ) n ) = 4 1 4 3 ( 1 − ( 4 3 ) n ) = 3 ( 1 − ( 4 3 ) n )
ดังนั้น ลำดับของผลบวกย่อย 3 4 + 9 16 + 27 64 + ⋯ + ( 3 4 ) n + ⋯ \displaystyle \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots + \left(\frac{3}{4}\right)^n + \cdots 4 3 + 16 9 + 64 27 + ⋯ + ( 4 3 ) n + ⋯ S n = 3 ( 1 − ( 3 4 ) n ) S_n = 3 \left(1-\left(\displaystyle \frac{3}{4}\right)^n\right) S n = 3 ( 1 − ( 4 3 ) n )
ต่อไปจะพิจารณาว่า อนุกรม 3 4 + 9 16 + 27 64 + ⋯ + ( 3 4 ) n + ⋯ \displaystyle \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots + \left(\frac{3}{4}\right)^n + \cdots 4 3 + 16 9 + 64 27 + ⋯ + ( 4 3 ) n + ⋯
lim n → ∞ S n = lim n → ∞ 3 ( 1 − ( 3 4 ) n ) = 3 ( 1 − lim n → ∞ ( 3 4 ) n ) \displaystyle\lim_{n\to\infty} S_n = \displaystyle\lim_{n\to\infty}3 \left(1-\left(\displaystyle \frac{3}{4}\right)^n\right) = 3\left(1-\displaystyle\lim_{n\to\infty}\left(\displaystyle \frac{3}{4}\right)^n\right) n → ∞ lim S n = n → ∞ lim 3 ( 1 − ( 4 3 ) n ) = 3 ( 1 − n → ∞ lim ( 4 3 ) n )
จากทฤษฎีบท 2 (ข้อ 1) จะได้ว่า lim n → ∞ ( 3 4 ) n = 0 \displaystyle\lim_{n\to\infty} \left(\displaystyle \frac{3}{4}\right)^n = 0 n → ∞ lim ( 4 3 ) n = 0 ดังนั้น lim n → ∞ S n = 3 ( 1 − 0 ) = 3 \displaystyle\lim_{n\to\infty} S_n = 3(1-0) = 3 n → ∞ lim S n = 3 ( 1 − 0 ) = 3
เพราะฉะนั้น อนุกรม 3 4 + 9 16 + 27 64 + ⋯ + ( 3 4 ) n + ⋯ \displaystyle \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots + \left(\frac{3}{4}\right)^n + \cdots 4 3 + 16 9 + 64 27 + ⋯ + ( 4 3 ) n + ⋯
ทฤษฎีบท 4 กำหนดให้อนุกรมเรขาคณิตมีพจน์ที่ 1 1 1 a 1 a_1 a 1 r r r (1) ถ้า ∣ r ∣ < 1 \left|r\right|<1 ∣ r ∣ < 1 a 1 1 − r \displaystyle\frac{a_1}{1-r} 1 − r a 1 (2) ถ้า ∣ r ∣ ≥ 1 \left|r\right|\geq 1 ∣ r ∣ ≥ 1
การเขียนอนุกรมจะใช้ตัวอักษรภาษากรีก ∑ \displaystyle\sum ∑ อนุกรมจำกัด a 1 + a 2 + a 3 + ⋯ + a n a_1+a_2+a_3+\cdots+a_n a 1 + a 2 + a 3 + ⋯ + a n ∑ i = 1 n a i \displaystyle\sum_{i=1}^{n}a_i i = 1 ∑ n a i อนุกรมอนันต์ a 1 + a 2 + a 3 + ⋯ + a n + ⋯ a_1+a_2+a_3+\cdots+a_n+\cdots a 1 + a 2 + a 3 + ⋯ + a n + ⋯ ∑ i = 1 ∞ a i \displaystyle\sum_{i=1}^{\infty}a_i i = 1 ∑ ∞ a i
ทฤษฎีบท 5 ให้ n n n (1) ∑ i = 1 n c = c n \displaystyle\sum_{i=1}^{n}c = cn i = 1 ∑ n c = c n (2) ∑ i = 1 n c a i = c ∑ i = 1 n a i \displaystyle\sum_{i=1}^{n}ca_i = c\displaystyle\sum_{i=1}^{n}a_i i = 1 ∑ n c a i = c i = 1 ∑ n a i (3) ∑ i = 1 n ( a i + b i ) = ∑ i = 1 n a i + ∑ i = 1 n b i \displaystyle\sum_{i=1}^{n}(a_i+b_i) = \displaystyle\sum_{i=1}^{n}a_i + \displaystyle\sum_{i=1}^{n}b_i i = 1 ∑ n ( a i + b i ) = i = 1 ∑ n a i + i = 1 ∑ n b i (4) ∑ i = 1 n ( a i − b i ) = ∑ i = 1 n a i − ∑ i = 1 n b i \displaystyle\sum_{i=1}^{n}(a_i-b_i) = \displaystyle\sum_{i=1}^{n}a_i - \displaystyle\sum_{i=1}^{n}b_i i = 1 ∑ n ( a i − b i ) = i = 1 ∑ n a i − i = 1 ∑ n b i
ทฤษฎีบท 6 ให้ n n n (1) ∑ i = 1 n i = n ( n + 1 ) 2 \displaystyle\sum_{i=1}^{n} i = \displaystyle\frac{n(n+1)}{2} i = 1 ∑ n i = 2 n ( n + 1 ) (2) ∑ i = 1 n i 2 = n ( n + 1 ) ( 2 n + 1 ) 6 \displaystyle\sum_{i=1}^{n} i^2 = \displaystyle\frac{n(n+1)(2n+1)}{6} i = 1 ∑ n i 2 = 6 n ( n + 1 ) ( 2 n + 1 ) (3) ∑ i = 1 n i 3 = ( n ( n + 1 ) 2 ) 2 = ( ∑ i = 1 n i ) 2 \displaystyle\sum_{i=1}^{n} i^3 = \left(\displaystyle\frac{n(n+1)}{2}\right)^2 = \left(\displaystyle\sum_{i=1}^{n} i\right)^2 i = 1 ∑ n i 3 = ( 2 n ( n + 1 ) ) 2 = ( i = 1 ∑ n i ) 2
Ex. จงหาผลบวก 10 10 10 ∑ i = 1 n ( 3 i − 1 ) 2 \displaystyle \sum_{i=1}^{n} (3i - 1)^2 i = 1 ∑ n ( 3 i − 1 ) 2 วิธีทำ
S 10 = ∑ i = 1 10 ( 3 i − 1 ) 2 = ∑ i = 1 10 ( 3 i ) 2 − 2 ( 3 i ) ( 1 ) + ( 1 ) 2 = ∑ i = 1 10 9 i 2 − 6 i + 1 = 9 ∑ i = 1 10 i 2 − 6 ∑ i = 1 10 i + ∑ i = 1 10 1 = 9 ( 10 ( 10 + 1 ) ( 2 ( 10 ) + 1 ) 6 ) − 6 ( 10 ( 10 + 1 ) 2 ) + 10 ( 1 ) = ( 3 ) ( 5 ) ( 11 ) ( 21 ) − ( 3 ) ( 10 ) ( 11 ) + 10 = 3 , 465 − 330 + 10 = 3 , 145 \begin{align*} S_{10} &= \displaystyle \sum_{i=1}^{10} (3i - 1)^2 \\ &= \displaystyle \sum_{i=1}^{10} (3i)^2 - 2(3i)(1) + (1)^2 \\ &= \displaystyle \sum_{i=1}^{10} 9i^2 - 6i + 1 \\ &= 9 \displaystyle \sum_{i=1}^{10}i^2 - 6\displaystyle \sum_{i=1}^{10}i + \displaystyle \sum_{i=1}^{10} 1 \\ &= 9 \left(\displaystyle\frac{10(10+1)(2(10)+1)}{6}\right) - 6\left(\displaystyle\frac{10(10+1)}{2}\right) + 10(1) \\ &= (3)(5)(11)(21) - (3)(10)(11) + 10 \\ &= 3,465 - 330 + 10 \\ &= 3,145 \end{align*} S 10 = i = 1 ∑ 10 ( 3 i − 1 ) 2 = i = 1 ∑ 10 ( 3 i ) 2 − 2 ( 3 i ) ( 1 ) + ( 1 ) 2 = i = 1 ∑ 10 9 i 2 − 6 i + 1 = 9 i = 1 ∑ 10 i 2 − 6 i = 1 ∑ 10 i + i = 1 ∑ 10 1 = 9 ( 6 10 ( 10 + 1 ) ( 2 ( 10 ) + 1 ) ) − 6 ( 2 10 ( 10 + 1 ) ) + 10 ( 1 ) = ( 3 ) ( 5 ) ( 11 ) ( 21 ) − ( 3 ) ( 10 ) ( 11 ) + 10 = 3 , 465 − 330 + 10 = 3 , 145
Ex. จงพิจารณาว่าอนุกรม ∑ n = 1 ∞ e − ( n + 1 ) \displaystyle \sum_{n=1}^{\infty} e^{-(n+1)} n = 1 ∑ ∞ e − ( n + 1 ) วิธีทำ จากอนุกรม ∑ n = 1 ∞ e − ( n + 1 ) = e − 2 + e − 3 + e − 4 + ⋯ + e − ( n + 1 ) + ⋯ \displaystyle \sum_{n=1}^{\infty} e^{-(n+1)} =e^{-2}+e^{-3}+e^{-4}+\cdots+e^{-(n+1)}+\cdots n = 1 ∑ ∞ e − ( n + 1 ) = e − 2 + e − 3 + e − 4 + ⋯ + e − ( n + 1 ) + ⋯ จะสังเกตว่า อัตราส่วนร่วม r = e − 3 e − 2 = 1 e 3 − 2 = 1 e r=\displaystyle\frac{e^{-3}}{e^{-2}} = \displaystyle\frac{1}{e^{3-2}} = \displaystyle\frac{1}{e} r = e − 2 e − 3 = e 3 − 2 1 = e 1 เนื่องจาก e ≈ 2.71828 > 1 e \approx 2.71828 > 1 e ≈ 2.71828 > 1 1 e < 1 \displaystyle\frac{1}{e} < 1 e 1 < 1 r < 1 r < 1 r < 1 โดยทฤษฎีบท 4 (ข้อ 1) จะได้ว่า อนุกรม ∑ n = 1 ∞ e − ( n + 1 ) \displaystyle \sum_{n=1}^{\infty} e^{-(n+1)} n = 1 ∑ ∞ e − ( n + 1 ) และผลบวกของอนุกรมเท่ากับ a 1 1 − r = e − 2 1 − 1 e = 1 e 2 ⋅ ( e − 1 e ) = 1 e 2 − e \displaystyle\frac{a_1}{1-r} = \displaystyle\frac{e^{-2}}{1-\displaystyle\frac{1}{e}} = \displaystyle\frac{1}{e^2\cdot\left(\displaystyle\frac{e-1}{e}\right)}= \displaystyle\frac{1}{e^2-e} 1 − r a 1 = 1 − e 1 e − 2 = e 2 ⋅ ( e e − 1 ) 1 = e 2 − e 1
ให้ a 1 , a 2 , a 3 , … , a n , … a_1, a_2, a_3, \dots, a_n, \dots a 1 , a 2 , a 3 , … , a n , … ถ้า a 28 2 − a 25 2 = 96 a_{28}^2 - a_{25}^2 = 96 a 28 2 − a 25 2 = 96 a 29 2 − a 24 2 a_{29}^2 - a_{24}^2 a 29 2 − a 24 2
120 120 120 144 144 144 160 160 160 200 200 200 250 250 250 วิธีทำ เนื่องจาก a 1 , a 2 , a 3 , … , a n , … a_1, a_2, a_3, \dots, a_n, \dots a 1 , a 2 , a 3 , … , a n , … d d d
a 28 2 − a 25 2 = 96 ( a 28 − a 25 ) ( a 28 + a 25 ) = 96 \begin{align*} a_{28}^2 - a_{25}^2 &= 96 \\ (a_{28}-a_{25})(a_{28}+a_{25}) &= 96 \\ \end{align*} a 28 2 − a 25 2 ( a 28 − a 25 ) ( a 28 + a 25 ) = 96 = 96
เนื่องจาก a 28 = a 25 + 3 d a_{28}=a_{25}+3d a 28 = a 25 + 3 d a 28 − a 25 = 3 d a_{28}-a_{25}=3d a 28 − a 25 = 3 d
( a 28 − a 25 ) ( a 28 + a 25 ) = 96 3 d ( a 28 + a 25 ) = 96 d ( a 28 + a 25 ) = 32 \begin{align*} (a_{28}-a_{25})(a_{28}+a_{25}) &= 96 \\ 3d(a_{28}+a_{25}) &= 96 \\ d(a_{28}+a_{25}) &= 32 \\ \end{align*} ( a 28 − a 25 ) ( a 28 + a 25 ) 3 d ( a 28 + a 25 ) d ( a 28 + a 25 ) = 96 = 96 = 32
ต่อไปจะพิจารณา a 29 2 − a 24 2 a_{29}^2 - a_{24}^2 a 29 2 − a 24 2 เนื่องจาก a 29 = a 24 + 5 d a_{29}=a_{24}+5d a 29 = a 24 + 5 d a 29 − a 24 = 5 d a_{29}-a_{24}=5d a 29 − a 24 = 5 d
a 29 2 − a 24 2 = ( a 29 − a 24 ) ( a 29 + a 24 ) = 5 d ( a 29 + a 24 ) = 5 d ( ( a 28 + d ) + ( a 25 − d ) ) = 5 d ( a 28 + a 25 + d − d ) = 5 ⋅ d ( a 28 + a 25 ) = 5 ⋅ 32 = 160 \begin{align*} a_{29}^2 - a_{24}^2 &= (a_{29}-a_{24})(a_{29}+a_{24}) \\ &= 5d(a_{29}+a_{24})\\ &= 5d((a_{28}+d)+(a_{25}-d))\\ &= 5d(a_{28}+a_{25}+d-d)\\ &= 5\cdot d(a_{28}+a_{25})\\ &= 5\cdot 32\\ &= 160 \end{align*} a 29 2 − a 24 2 = ( a 29 − a 24 ) ( a 29 + a 24 ) = 5 d ( a 29 + a 24 ) = 5 d (( a 28 + d ) + ( a 25 − d )) = 5 d ( a 28 + a 25 + d − d ) = 5 ⋅ d ( a 28 + a 25 ) = 5 ⋅ 32 = 160
ตอบ ข้อ 3. 160 160 160