
สถิติ
มกราคม 10, 2026
สวัสดีค้าบบ สำหรับบทนี้พี่แม็คจะมาสรุปเนื้อหาในเรื่องสถิติครบทุกเรื่อง ตั้งแต่ความรู้พื้นฐานของสถิติศาสตร์ การแบ่งประเภทของข้อมูล การวิเคราะห์และนำเสนอข้อมูลเชิงคุณภาพและข้อมูลเชิงปริมาณ ตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ซึ่งพี่แม็คได้สรุปสูตรพื้นฐานและตัวอย่างสั้น ๆ สำหรับทบทวนก่อนสอบให้เข้าใจได้ง่าย ดังนี้ค้าบบ
สถิติศาสตร์
สถิติศาสตร์ (Statistics) เป็นวิชาที่ว่าด้วยการเก็บรวบรวมข้อมูล การวิเคราะห์ข้อมูล และสรุปผลจากข้อมูลที่เกี่ยวข้อง เพื่อนำมาตอบคำถามและประเด็นที่สนใจ
คำสำคัญในสถิติศาสตร์
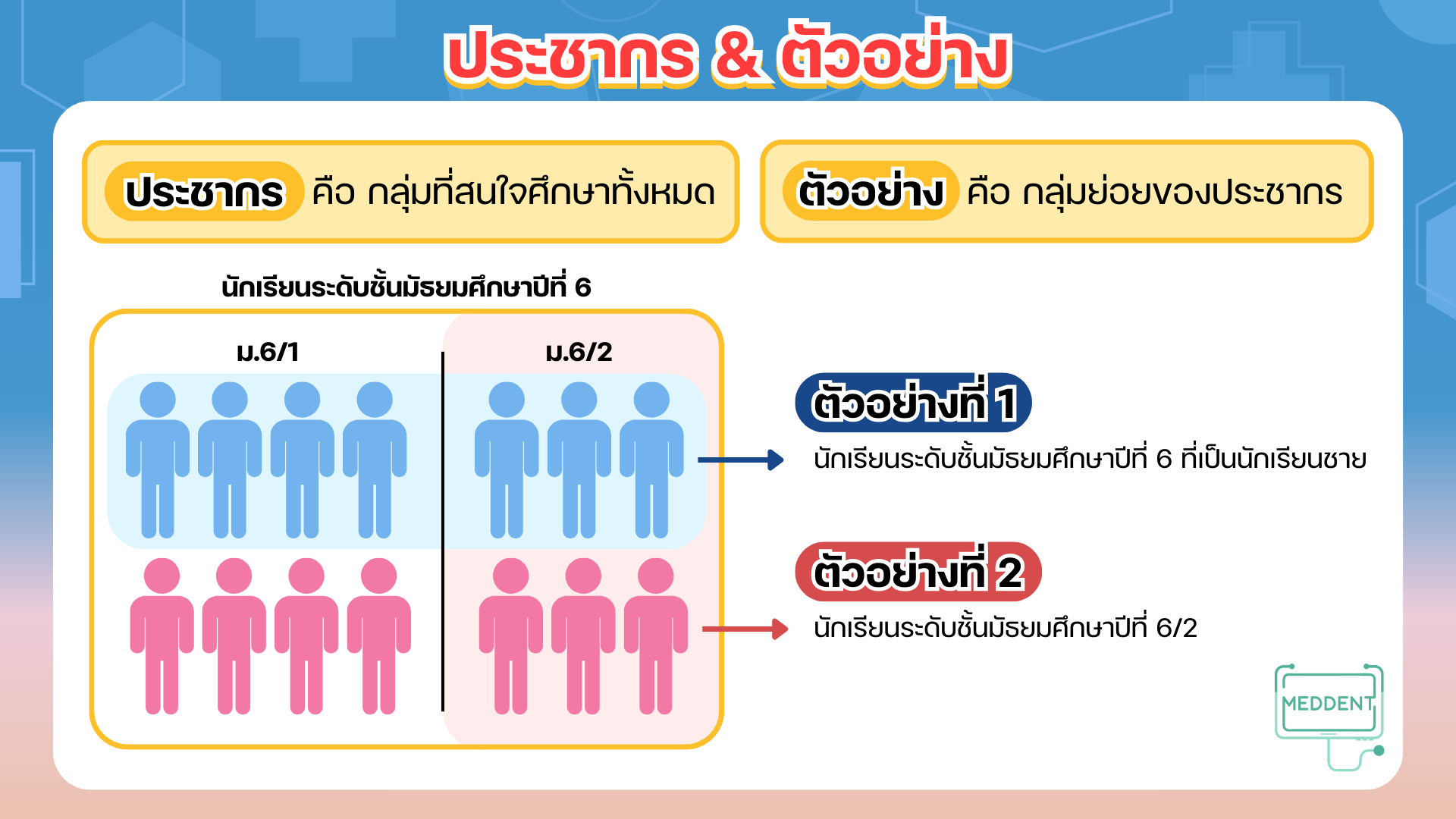
ประชากร (population) คือ กลุ่มที่สนใจศึกษาทั้งหมด
ตัวอย่าง (sample) คือ กลุ่มย่อยของประชากร
Ex. ถ้ากำหนดให้ประชากรเป็นนักเรียนระดับชั้นมัธยมศึกษาปีที่ แล้วต้องการทราบว่า นักเรียนชอบเรียนวิชาใดมากที่สุด อาจจะกำหนดตัวอย่างได้เป็น
- นักเรียนระดับชั้นมัธยมศึกษาปีที่ ที่เป็นนักเรียนชาย
- นักเรียนระดับชั้นมัธยมศึกษาปีที่
ตัวแปร (variable) คือ สิ่งที่สนใจศึกษา เช่น เพศ อายุ ระดับการศึกษา รายได้
ข้อมูล (data) คือ ค่าของตัวแปรที่สนใจศึกษา (จะเป็นตัวเลขหรือไม่ก็ได้)
Ex. จากการสอบถามนักเรียนระดับชั้นมัธยมศึกษาปีที่ ว่า นักเรียนชอบเรียนวิชาใดมากที่สุด จะเห็นว่า
ตัวแปร คือ วิชาที่น้อง ๆ ชอบเรียน
ข้อมูล จะเป็นวิชาที่น้อง ๆ เรียน เช่น คณิตศาสตร์ วิทยาศาสตร์ ภาษาไทย ภาษาอังกฤษ สังคมศึกษา เป็นต้น
พารามิเตอร์ (parameter) คือ ค่าวัดที่แสดงลักษณะของประชากร ซึ่งเป็นค่าคงตัวที่คำนวณ หรือประมวลจากข้อมูลทั้งหมดของประชากร
ค่าสถิติ (statistic) คือ เป็นค่าคงตัวที่พิจารณาจากข้อมูลของตัวอย่าง โดยมีวัตถุประสงค์เพื่ออธิบายลักษณะของตัวอย่างนั้นหรือเพื่อประมาณค่าของพารามิเตอร์แล้วนำไปใช้ในการอธิบายลักษณะของประชากร
Ex. อาจารย์เก็บคะแนนเรื่องสถิติโดยการสอบย่อย คะแนน พบว่า นักเรียนทั้งระดับชั้นมัธยมศึกษาปีที่
สอบได้คะแนนเฉลี่ยอยู่ที่ คะแนน และนักเรียน ม. และ ม. สอบได้คะแนนเฉลี่ยอยู่ที่ และ คะแนน
ตามลำดับ จะได้ว่า
พารามิเตอร์ คือ คะแนนเฉลี่ยของนักเรียนทั้งระดับชั้นมัธยมศึกษาปีที่
ค่าสถิติ คือ คะแนนเฉลี่ยของนักเรียน ม. และ ม.
ประเภทของข้อมูล
1. แบ่งตามแหล่งที่มา
ข้อมูลปฐมภูมิ (primary data) คือ ข้อมูลที่ได้เก็บมาเองโดยตรง
ข้อมูลทุติยภูมิ (secondary data) คือ ข้อมูลที่ได้เก็บมาจากคนอื่น หรือหน่วยงานอื่นอีกที
Ex. อาจารย์เก็บคะแนนเรื่องสถิติโดยการสอบย่อย คะแนน
ถ้าอาจารย์นำคะแนนสอบของนักเรียนแต่ละคนมาหาค่าเฉลี่ยซึ่งได้ คะแนน จะได้ว่า ข้อมูลนี้เป็นข้อมูลปฐมภูมิ
แต่ถ้าเติร์ดเป็นนักเรียนที่นำคะแนนสอบของตัวเองเปรียบเทียบกับค่าเฉลี่ยแล้วพบว่า เติร์ดเป็นคนที่ได้คะแนนมากกว่าค่าเฉลี่ยอยู่ คะแนน จะได้ว่า ข้อมูลนี้เป็นข้อมูลทุติยภูมิ
2. แบ่งตามระยะเวลาที่จัดเก็บ
ข้อมูลอนุกรมเวลา (time series data) คือ ข้อมูลที่เกิดขึ้นและจัดเก็บตามลำดับเวลาต่อเนื่องกันไป
ข้อมูลตัดขวาง (cross-sectional data) คือ ข้อมูล ณ จุดหนึ่งของเวลา
Ex. กรมควบคุมมลพิษได้เก็บข้อมูลปริมาณฝุ่น PM2.5 ตั้งแต่ปี พ.ศ. จนถึงปัจจุบัน จะได้ว่า ข้อมูลนี้เป็นข้อมูลอนุกรมเวลา
ถ้ากรมควบคุมมลพิษได้นำเสนอข้อมูลปริมาณฝุ่น PM2.5 ในวันที่ ธันวาคม จะได้ว่า ข้อมูลนี้เป็นข้อมูลตัดขวาง
3. แบ่งตามลักษณะของข้อมูล
ข้อมูลเชิงปริมาณ (quantitative data) คือ ข้อมูลที่ได้จากการวัดค่า แสดงเป็นตัวเลขหรือปริมาณที่สามารถนำไป บวก ลบ คูณ หรือหาร และเปรียบเทียบ (มากกว่า/น้อยกว่า) กันได้
ข้อมูลเชิงคุณภาพ (qualitative data) คือ ข้อมูลที่แสดงลักษณะ ประเภท สมบัติ ไม่สามารถวัดค่าเป็นตัวเลขที่นำมาบวก ลบ คูณ หรือหารกันได้
Ex. อาจารย์เก็บคะแนนเรื่องสถิติโดยการสอบย่อย คะแนน พบว่า นักเรียนทั้งระดับชั้นมัธยมศึกษาปีที่ ในที่นี้ข้อมูลที่ได้จะเป็นตัวเลขที่อยู่ในช่วงปิด ดังนั้น ข้อมูลนี้เป็นข้อมูลเชิงปริมาณ
จากการสอบถามนักเรียนระดับชั้นมัธยมศึกษาปีที่ ว่า นักเรียนชอบเรียนวิชาใดมากที่สุด ในที่นี้ข้อมูลที่ได้จะเป็นวิชาที่ชอบเรียน เช่น คณิตศาสตร์ ภาษาอังกฤษ สังคมศึกษา เป็นต้น ดังนั้น ข้อมูลนี้เป็นข้อมูลเชิงคุณภาพ
การวิเคราะห์และนำเสนอข้อมูลเชิงคุณภาพ
ฐานนิยม (mode) นั่นคือ ข้อมูลที่มีจำนวนครั้งของการเกิดซ้ำกันมากที่สุด
ความถี่ (frequency) คือ จำนวนครั้งของการเกิดข้อมูลข้อมูลหนึ่ง
ความถี่สัมพัทธ์ (relative frequency) คือ สัดส่วนของความถี่ของแต่ละข้อมูลเทียบกับความถี่ทั้งหมด
Ex. จากการสอบถามนักเรียนระดับชั้นมัธยมศึกษาปีที่ จำนวน คน เกี่ยวกับความชอบเรียนวิชาใดมากที่สุด ซึ่งผลการสำรวจเป็นดังนี้
จากข้อมูลข้างต้นสามารถนำเสนอข้อมูลด้วยตารางความถี่ ดังนี้
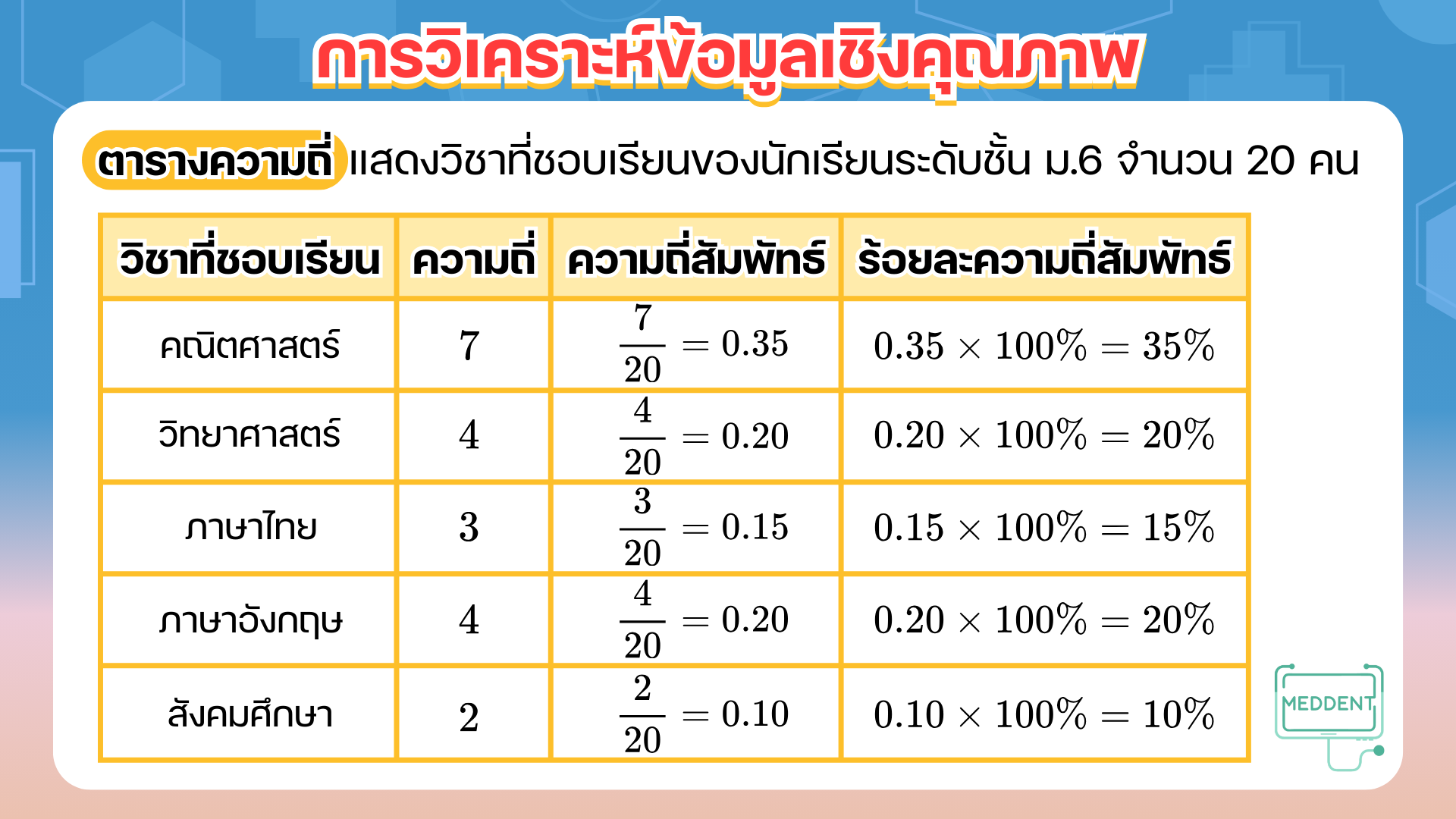
ข้อมูลต่าง ๆ ของข้อมูลเชิงคุณภาพที่จะนำมาวิเคราะห์ส่วนใหญ่แล้วจะวิเคราะห์โดยพิจารณาจากความถี่สัมพัทธ์ แล้วนำมาคิดเป็นเปอร์เซ็นต์ตามที่น้อง ๆ เห็นได้ในตารางเลยคั้บ^^
นอกจากการวิเคราะห์ข้อมูลด้วยความถี่สัมพัทธ์แล้วเรายังสามารถวิเคราะห์ข้อมูลโดยใช้ฐานนิยม ซึ่งจากตารางน้อง ๆ สามารถสรุปได้เลยทันทีว่า วิชาคณิตศาสตร์เป็นวิชาที่นักเรียนที่ชอบมากที่สุดนั่นเองคร้าบบ
การนำเสนอข้อมูลเชิงคุณภาพสามารถทำได้หลายรูปแบบดังนี้

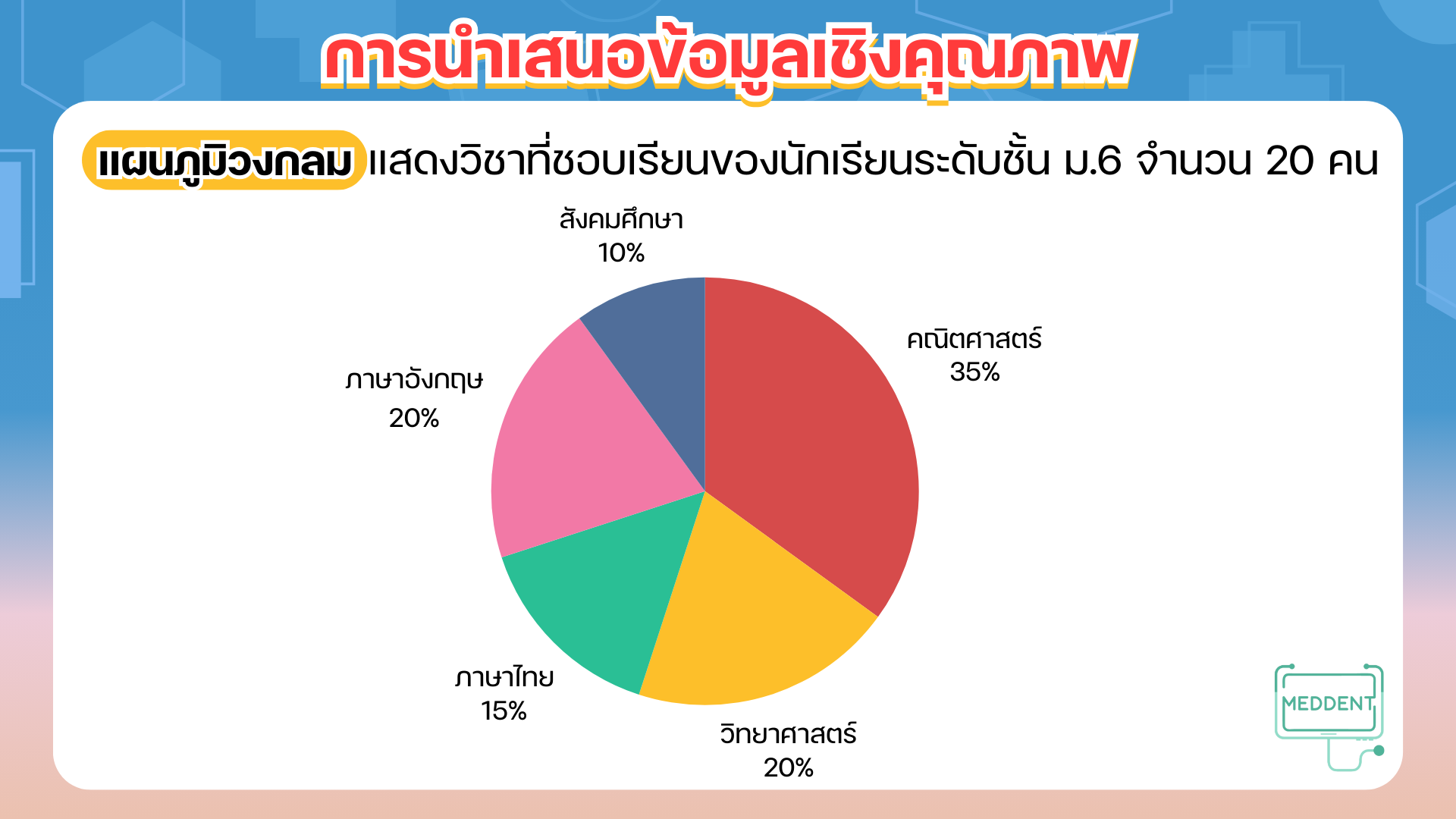
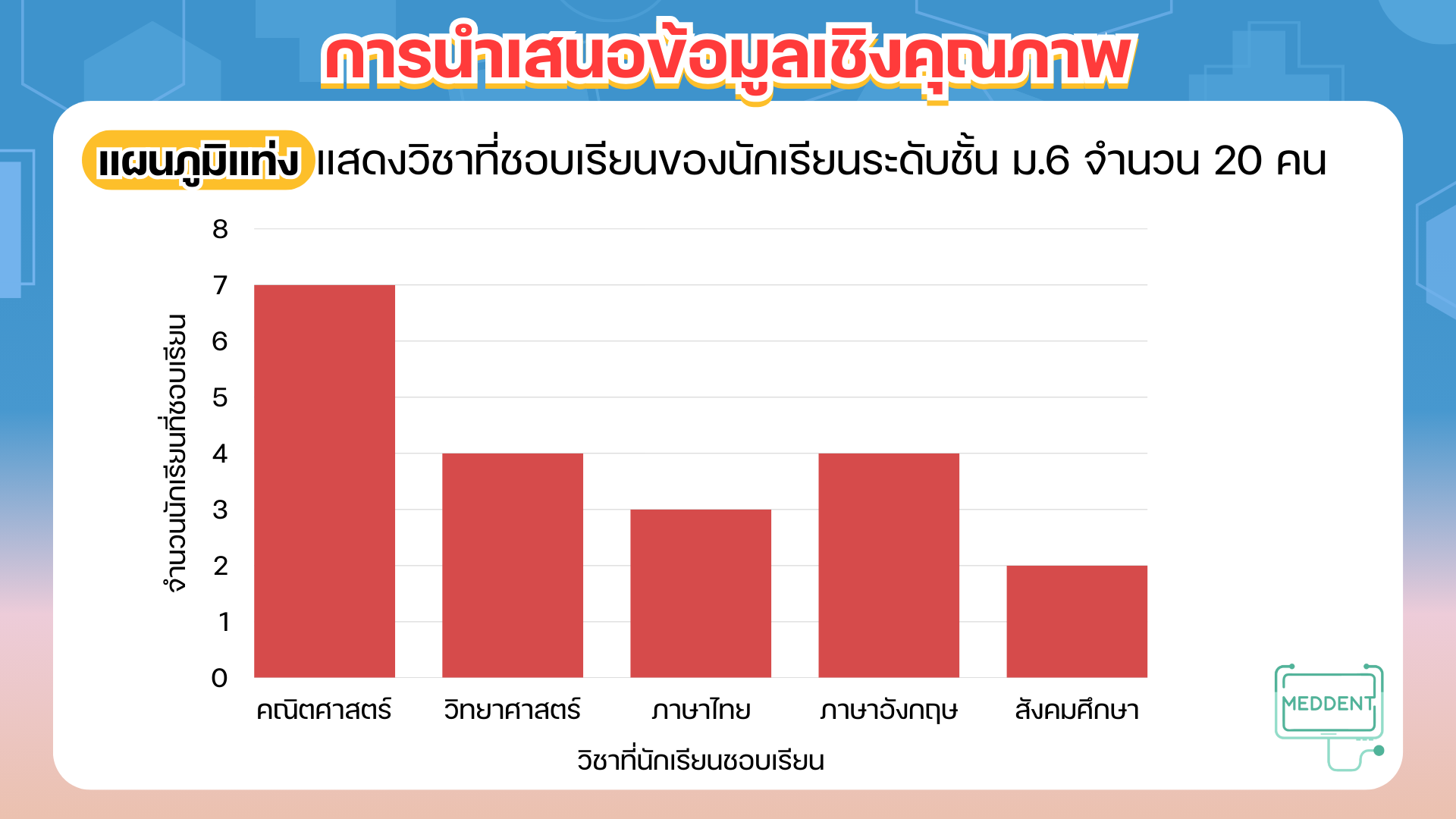
การวิเคราะห์และนำเสนอข้อมูลเชิงปริมาณ
Ex. การเก็บคะแนน Mock Test ของน้อง ๆ ที่เรียนกับพี่เหม่อสุดแล็ค พบว่าเป็นไปตามตารางดังนี้
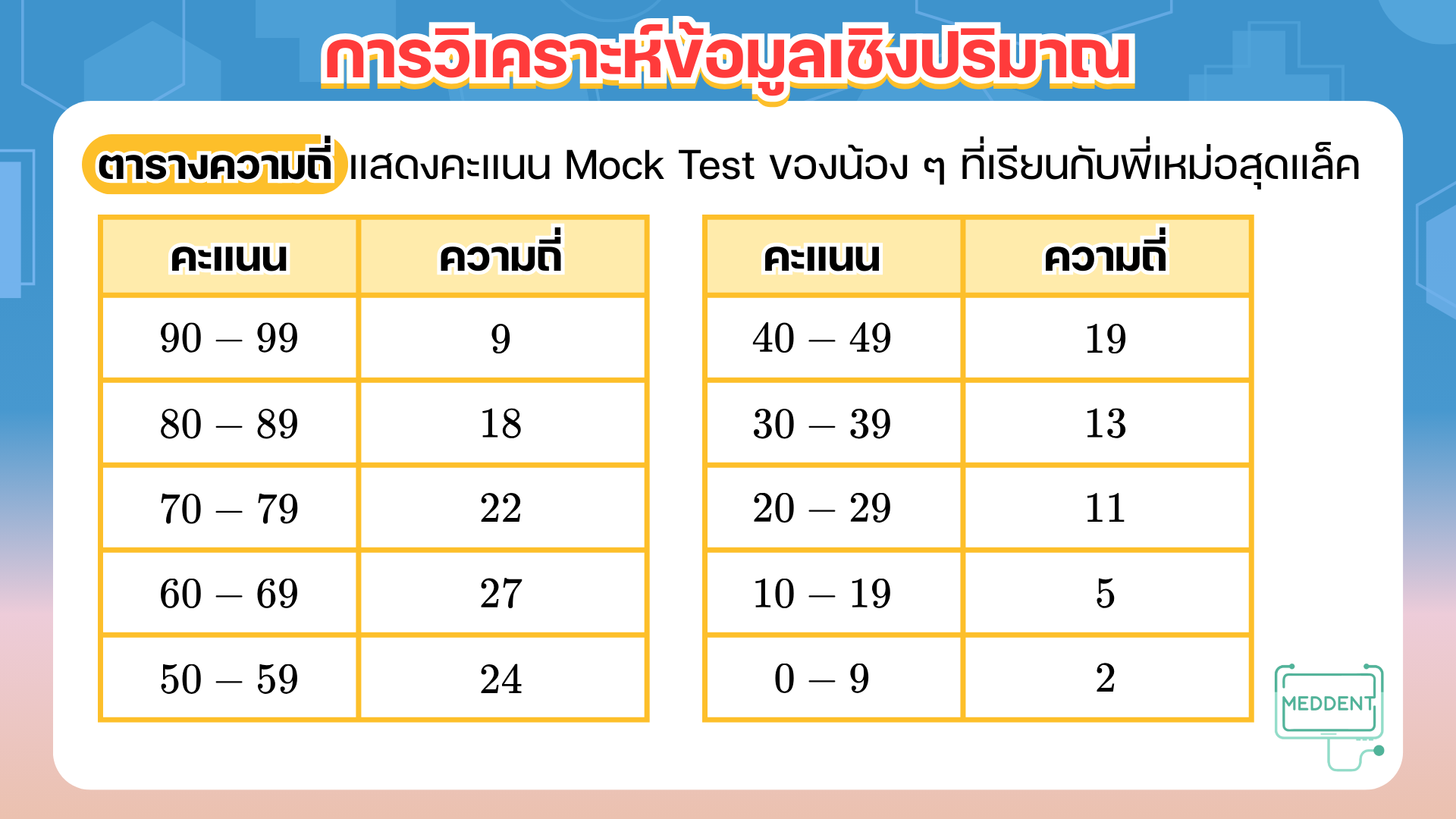
ตารางที่แสดงให้เห็นข้างต้นนี้ เรียกว่า ตารางความถี่แบบแบ่งข้อมูลเป็นช่วง
และเรียกคะแนนในแต่ละช่วงว่า อันตรภาคชั้น (class interval)
การนำเสนอข้อมูลเชิงปริมาณสามารถทำได้หลายรูปแบบดังนี้
1. ฮิสโทแกรม
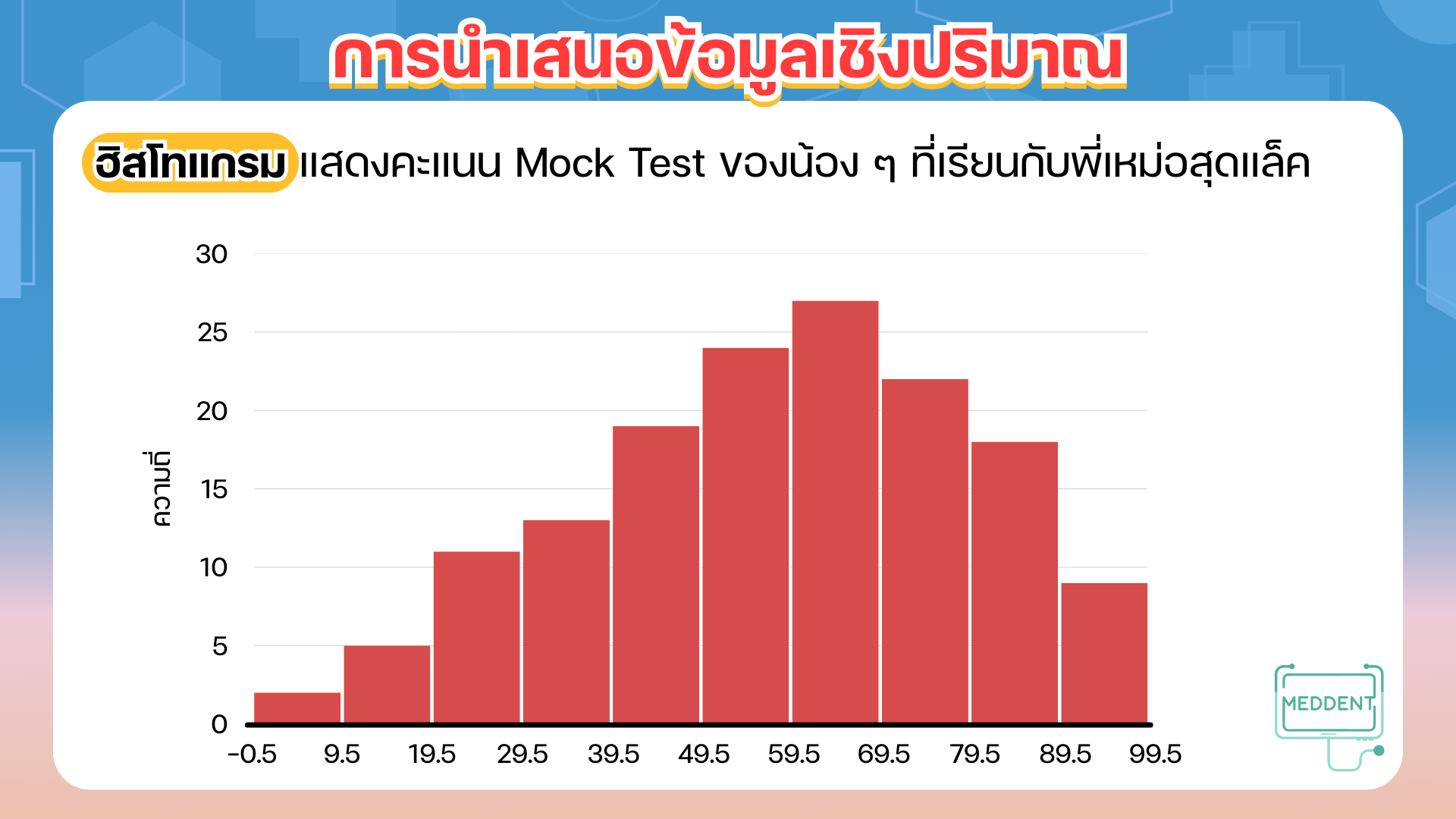
Ex. การสอบเก็บคะแนนวิชาสถิติของนักเรียนห้องหนึ่ง เป็นดังนี้
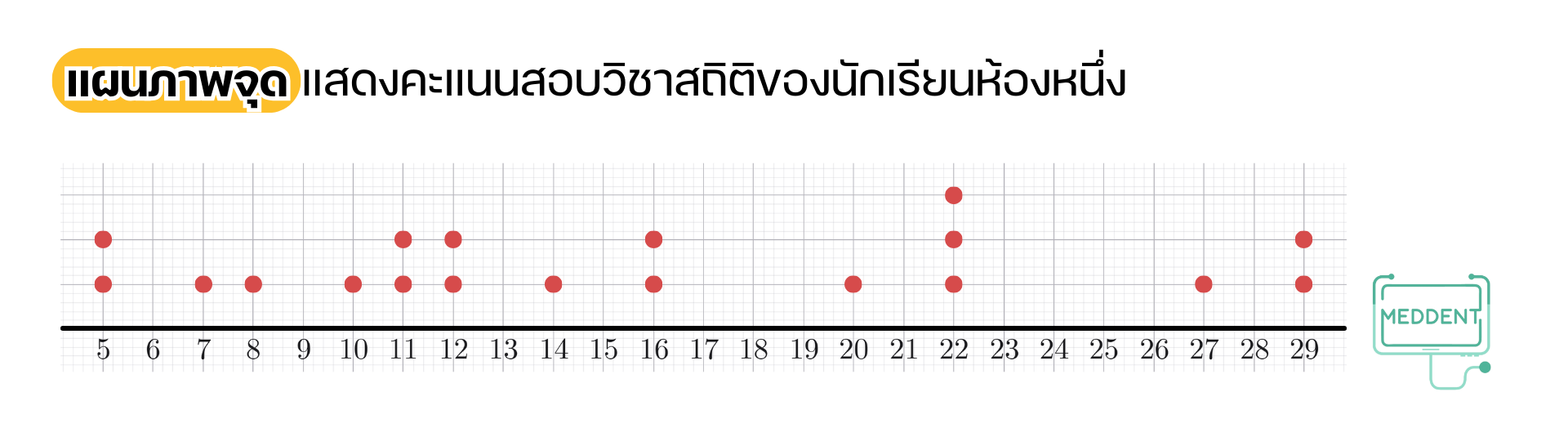
2. แผนภาพจุด เป็นแผนภาพที่แสดงจุดหรือวงกลมเล็ก ๆ แทนข้อมูลแต่ละตัว เหนือเส้นจำนวนแนวนอน
3. แผนภาพลำต้นและใบ เป็นแผนภาพที่ประกอบไปด้วย 2 ส่วนหลัก ๆ ได้แก่ ใบ ที่แทนหลักหน่วย และ ลำต้น แทนหลักสิบ, หลักร้อย, หลักพัน, …

4. แผนภาพกล่อง เป็นแผนภาพที่แสดงตำแหน่งของข้อมูลค่าสูงสุด ค่าต่ำสุด และควอร์ไทล์ต่าง ๆ
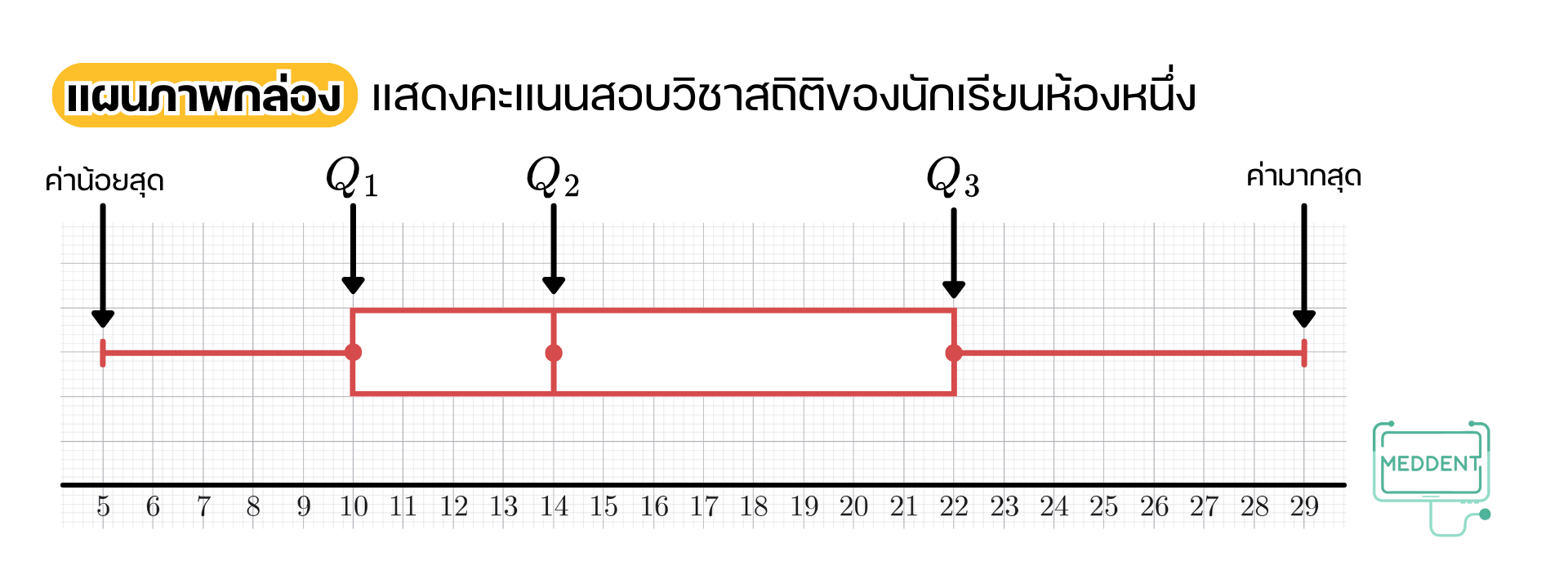
หากน้อง ๆ กำลังสงสัยว่า ควอร์ไทล์คืออะไร พี่แม็คสรุปให้เรียบร้อยแล้ว ดังนี้คั้บ ควอร์ไทล์ (quartile) : แบ่งข้อมูลที่เรียงจากน้อยไปมากออกเป็น 4 ส่วนเท่า ๆ กัน
STEPs การหาควอร์ไทล์
1. เรียงข้อมูลจากน้อยไปหามาก
2. ตำแหน่งของควอร์ไทล์ที่ คือ เมื่อ
3. ควอร์ไทล์ที่ จะอยู่ในตำแหน่งที่คิดมาได้
จากโจทย์สามารถหาควอร์ไทล์ที่ และ ได้ดังนี้
- เรียงข้อมูลจากน้อยไปหามาก จะได้ว่า
- ตำแหน่งของควอร์ไทล์ที่ คือ
ตำแหน่งของควอร์ไทล์ที่ คือ
ตำแหน่งของควอร์ไทล์ที่ คือ - ดังนั้น ควอร์ไทล์ที่ จะมีค่าเท่ากับข้อมูลตัวที่ นั่นคือ
ควอร์ไทล์ที่ จะมีค่าเท่ากับข้อมูลตัวที่ นั่นคือ
และควอร์ไทล์ที่ จะมีค่าเท่ากับข้อมูลตัวที่ นั่นคือ
ในการวาดแผนภาพกล่องน้อง ๆ จะต้องตรวจสอบค่าหนึ่งที่เรียกว่า ค่านอกเกณฑ์ (outlier) ซึ่งเป็นข้อมูลที่แตกต่างไปจากข้อมูลส่วนใหญ่มาก ๆ ดังนั้น ถ้าน้อง ๆ มีข้อมูลที่มีค่าน้อยกว่า หรือมีข้อมูลที่มีค่ามากกว่า ข้อมูลเหล่านี้จะถือว่าเป็นค่านอกเกณฑ์ทันทีเลยค้าบบ
จากแผนภาพกล่องจะเห็นว่า และ
จะได้ว่า
และ
นั่นคือ ข้อมูลที่มีค่าน้อยกว่า หรือข้อมูลที่มีค่ามากกว่า จะเป็นค่านอกเกณฑ์
ทำให้ได้ว่า ข้อมูลชุดนี้ไม่มีค่านอกเกณฑ์นั่นเองค้าบบ^^
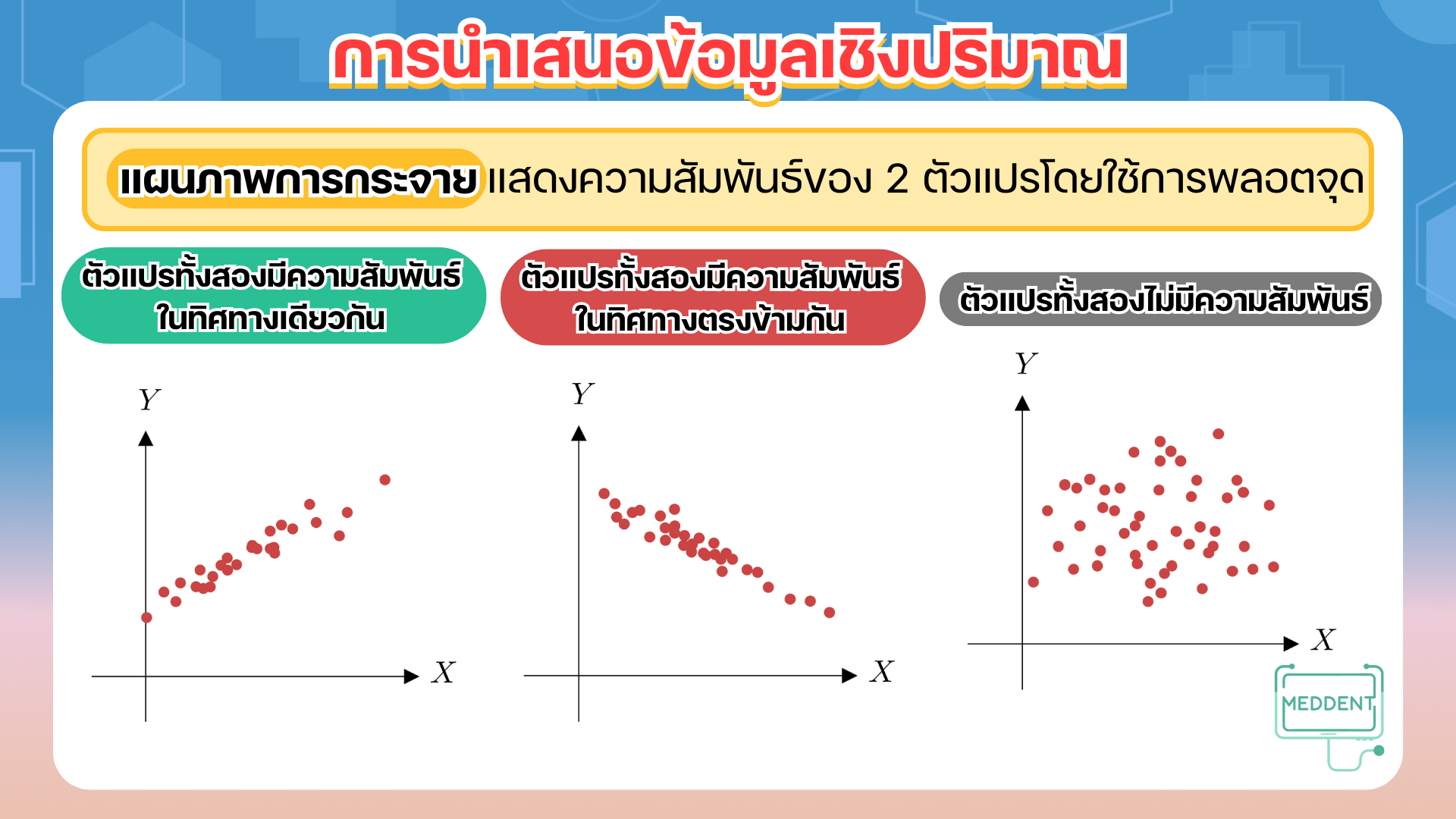
5. แผนภาพการกระจาย เป็นแผนภาพที่แสดงความสัมพันธ์ของข้อมูลเชิงปริมาณ ข้อมูล
ค่าวัดทางสถิติ
ค่าวัดทางสถิติเป็นสิ่งที่ช่วยทำให้เห็นภาพรวมของข้อมูลและทำให้จดจำข้อสรุปเกี่ยวกับข้อมูลได้ง่ายมากยิ่งขึ้น
1. ค่ากลางของข้อมูล
ค่ากลางของข้อมูลจะเป็นตัวแทนของข้อมูลทั้งหมด ได้แก่
1.1 ค่าเฉลี่ยเลขคณิต
ค่าเฉลี่ยเลขคณิต (arithmetic mean) : การนำข้อมูลทุกตัวมารวมกัน แล้วหารด้วยจำนวนข้อมูลทั้งหมด
ค่าเฉลี่ยเลขคณิตสามารถแบ่งได้เป็น 2 ประเภท คือ
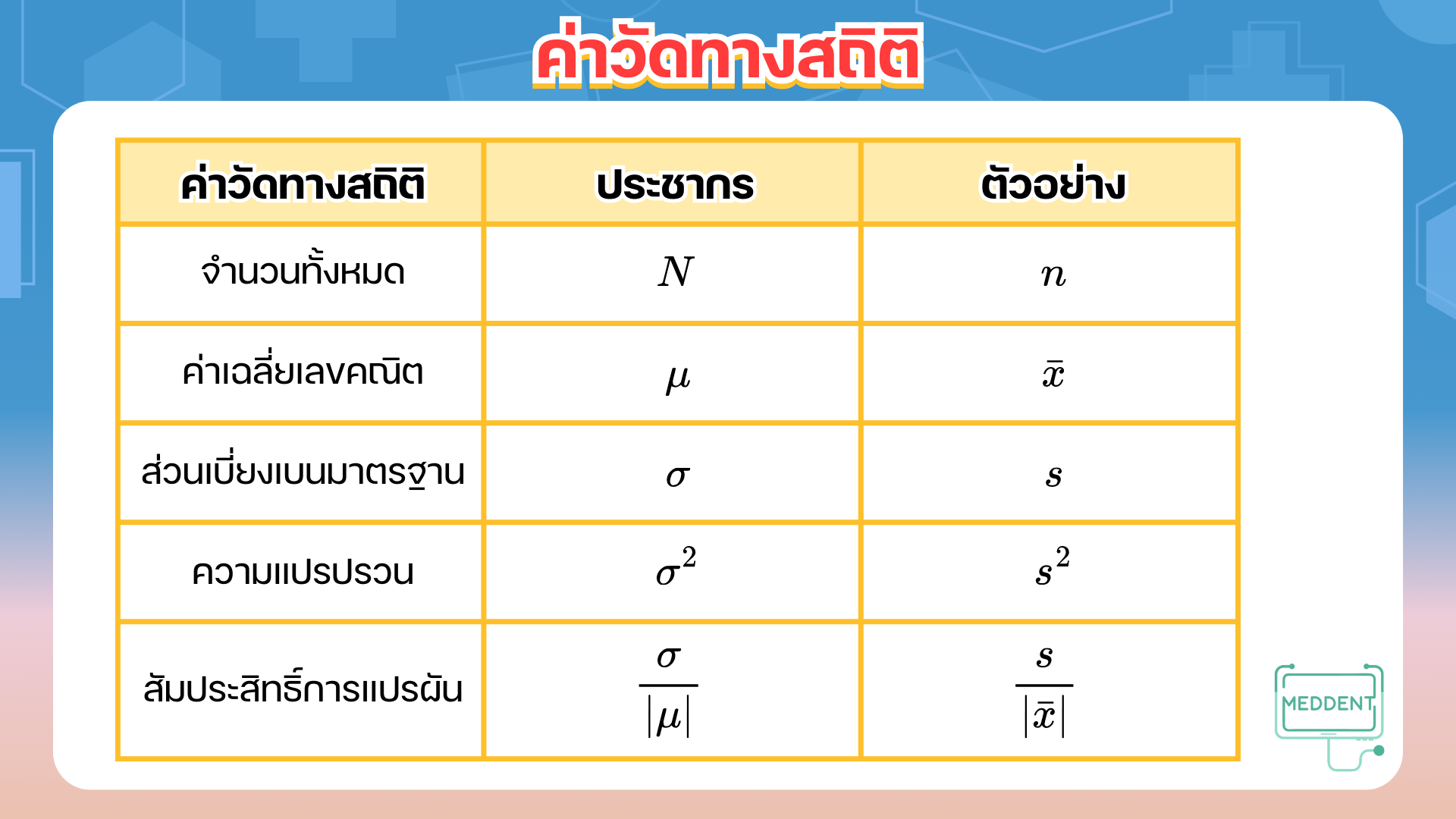
(i) ค่าเฉลี่ยเลขคณิตที่เป็นพารามิเตอร์ เขียนแทนด้วย ซึ่งเป็นค่าเฉลี่ยที่คำนวณจากข้อมูลของประชากร
ทั้งหมด ตัว นั่นคือ
(ii) ค่าเฉลี่ยเลขคณิตที่เป็นค่าสถิติ เขียนแทนด้วย ซึ่งเป็นค่าเฉลี่ยที่คำนวณจากข้อมูลของตัวอย่างทั้งหมด ตัว นั่นคือ
1.2 มัธยฐาน
มัธยฐาน (median) : ค่าที่อยู่ในตำแหน่งกึ่งกลาง ต้องเรียงลำดับจากน้อยไปมากเสมอ!!
STEPs การหามัธยฐาน
1. เรียงข้อมูลจากน้อยไปหามาก
2. ตำแหน่งของมัธยฐาน คือ
3. มัธยฐานจะอยู่ในตำแหน่งที่คิดมาได้
1.3 ฐานนิยม
ฐานนิยม (mode) : ค่าที่ข้อมูลมีการซ้ำกันมากที่สุด
Ex. จากการสุ่มสอบถามนักเรียน คนที่สอบเก็บคะแนนวิชาสถิติของนักเรียนห้องหนึ่ง เป็นดังนี้
จงหาค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยมของข้อมูลชุดนี้
วิธีทำ (1) จะหาค่าเฉลี่ยเลขคณิต
เนื่องจากข้อมูลชุดนี้เป็นข้อมูลที่ได้จากการสุ่มสอบถามนักเรียนในห้องจำนวน คน ซึ่งเป็นข้อมูลที่เป็นตัวอย่าง ดังนั้น ค่าเฉลี่ยเลขคณิตของข้อมูลชุดนี้ คือ
(2) จะหามัธยฐาน
- เรียงข้อมูลจากน้อยไปหามาก จะได้ว่า
- ตำแหน่งของมัธยฐาน คือ
- ดังนั้น มัธยฐานจะมีค่าเท่ากับข้อมูลตัวที่ นั่นคือ
(3) ฐานนิยมมีค่าเท่ากับ เพราะว่า เป็นข้อมูลมีการซ้ำกันมากที่สุด
ดังนั้น ค่าเฉลี่ยเลขคณิตและมัธยฐานของข้อมูลชุดนี้เท่ากับ คะแนน และฐานนิยมมีค่าเท่ากับ
2. ค่าวัดการกระจาย
ค่าวัดการกระจายเป็นการดูการกระจายตัวของข้อมูล สามารถแบ่งได้เป็น
2.1 การกระจายสัมบูรณ์
การกระจายสัมบูรณ์ (absolute variation) : ใช้วัดข้อมูลแต่ละตัวมีความแตกต่างกันมากหรือน้อยอย่างไร ซึ่งมีดังนี้
(1) พิสัย (range) ค่ามากสุด ค่าน้อยสุด
(2) พิสัยระหว่างควอร์ไทล์ (interquartile range: IQR)
(3) ส่วนเบี่ยงเบนมาตรฐาน (standard deviation: SD) : ใช้วัดการกระจายของข้อมูลที่บอกว่าข้อมูลแต่ละตัวอยู่ห่างจากค่าเฉลี่ยเลขคณิตประมาณเท่าใด
ส่วนเบี่ยงเบนมาตรฐานสามารถแบ่งได้เป็น 2 ประเภท คือ
(i) ส่วนเบี่ยงเบนมาตรฐานที่เป็นพารามิเตอร์ เขียนแทนด้วย ซึ่งจะคิดจากข้อมูลของประชากร
ทั้งหมด ตัว นั่นคือ
(ii) ส่วนเบี่ยงเบนมาตรฐานที่เป็นค่าสถิติ เขียนแทนด้วย ซึ่งเป็นค่าเฉลี่ยที่คำนวณจากข้อมูลของตัวอย่าง
ทั้งหมด ตัว นั่นคือ
(4) ความแปรปรวน (variance) : กำลังสองของส่วนเบี่ยงเบนมาตรฐาน ความแปรปรวนสามารถแบ่งได้เป็น 2 ประเภท คือ
(i) ความแปรปรวนที่เป็นพารามิเตอร์ เขียนแทนด้วย
(ii) ความแปรปรวนที่เป็นค่าสถิติ เขียนแทนด้วย
Ex. จากการสอบถามอายุของผู้ที่เข้าใช้บริการในสนามเด็กเล่นแห่งหนึ่งในวันศุกร์ที่ สิงหาคม เวลา น. พบว่ามีผู้ที่เข้าใช้บริการในสนามเด็กเล่นทั้งหมด คน ซึ่งมีอายุเป็นดังนี้
จงหาพิสัย พิสัยระหว่างควอร์ไทล์ ส่วนเบี่ยงเบนมาตรฐาน และความแปรปรวนของข้อมูลชุดนี้
วิธีทำ เรียงข้อมูลจากน้อยไปหามาก จะได้ว่า
เนื่องจากพิสัยคือผลต่างระหว่างข้อมูลที่มีค่าสูงสุดและข้อมูลที่มีค่าต่ำสุด
ดังนั้น พิสัย
(2) จะหาพิสัยระหว่างควอร์ไทล์
- หาตำแหน่งของควอร์ไทล์ที่ และควอร์ไทล์ที่
- ดังนั้น คือข้อมูลตัวที่ มีค่าเท่ากับ และ คือข้อมูลตัวที่ มีค่าเท่ากับ
- จะได้พิสัยระหว่างควอร์ไทล์ คือ
(3) จะหาส่วนเบี่ยงเบนมาตรฐาน
เนื่องจากข้อมูลเป็นการสอบถามผู้เข้าใช้บริการสนามเด็กเล่นทั้งหมด คน นั่นคือ ข้อมูลชุดนี้เป็นข้อมูลของประชากร ทำให้ได้ว่า เราต้องหาค่าเฉลี่ยเลขคณิต ก่อน
จากสูตรส่วนเบี่ยงเบนมาตรฐานของประชากร
จะได้
(4) จะหาความแปรปรวน
เนื่องจากความแปรปรวนคือส่วนเบี่ยงเบนมาตรฐานยกกำลังสอง จะได้ว่า
เพราะฉะนั้น ข้อมูลชุดนี้มีพิสัยเท่ากับ ปี พิสัยระหว่างควอร์ไทล์เท่ากับ ปี
ส่วนเบี่ยงเบนมาตรฐานเท่ากับ ปี และความแปรปรวนเท่ากับ ปี
2.2 การกระจายสัมพัทธ์
การกระจายสัมพัทธ์ (relative variation) : ใช้เปรียบเทียบการกระจายของข้อมูล 2 ชุดขึ้นไป
สัมประสิทธิ์การแปรผัน (coefficient of variation: C.V.) สามารถแบ่งได้เป็น 2 ประเภท คือ
(i) สัมประสิทธิ์การแปรผันที่เป็นพารามิเตอร์ คิดจาก เมื่อ
(ii) สัมประสิทธิ์การแปรผันที่เป็นค่าสถิติ คิดจาก เมื่อ
Ex. จากการสอบถามอายุของผู้ที่เข้าใช้บริการทั้งหมดในสนามเด็กเล่นแห่งหนึ่ง พบว่าในวันศุกร์ที่ สิงหาคม เวลา น. มีผู้ที่เข้าใช้บริการในสนามเด็กเล่นแห่งนี้ คน ซึ่งมีอายุเป็นดังนี้
และวันเสาร์ที่ สิงหาคม เวลา น. พบว่ามีผู้ที่เข้าใช้บริการในสนามเด็กเล่นแห่งเดียวกันนี้ทั้งหมด คน ซึ่งมีอายุเป็นดังนี้
จงเปรียบเทียบการกระจายของข้อมูล 2 ชุดนี้
วิธีทำ กำหนดให้ เป็นอายุเฉลี่ยของผู้เข้าใช้บริการในวันที่ และ ตามลำดับ
และให้ เป็นส่วนเบี่ยงเบนมาตรฐานของผู้เข้าใช้บริการในวันที่ และ ตามลำดับ
จากตัวอย่างที่ผ่านมา พบว่า และ
ดังนั้น สัมประสิทธิ์การแปรผันของอายุผู้ใช้บริการในวันที่ เท่ากับ
ต่อไปจะหาสัมประสิทธิ์การแปรผันของอายุผู้ใช้บริการในวันที่ ดังนี้
- หาค่าเฉลี่ยเลขคณิต
- หาส่วนเบี่ยงเบนมาตรฐาน
ดังนั้น สัมประสิทธิ์การแปรผันของอายุผู้ใช้บริการในวันที่ เท่ากับ
จะเห็นว่า สัมประสิทธิ์การแปรผันของอายุผู้ใช้บริการในวันที่ มากกว่าวันที่
เพราะฉะนั้น ข้อมูลอายุผู้ใช้บริการในวันที่ จะมีการกระจายของข้อมูลอายุมากกว่าวันที่
ต่อไปพี่แม็คจะพูดถึงเรื่องตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ซึ่งพี่แม็คแนะนำว่าให้น้อง ๆ ทบทวนความรู้เรื่องการทดลองสุ่ม ปริภูมิตัวอย่าง เหตุการณ์ และความน่าจะเป็น สามารถกดได้ที่นี่เลยคร้าบบ แต่ถ้าเกิดว่าน้องแม่นเนื้อหาเรื่องความน่าจะเป็นแล้ว น้องลุยเรื่องตัวแปรสุ่มและการแจกแจงความน่าจะเป็นต่อได้เลยค้าบบ
ตัวแปรสุ่ม
ตัวแปรสุ่ม (random variable) : ฟังก์ชันจากปริภูมิตัวอย่างของการทดลองสุ่มไปยังเซตของจำนวนจริง
ตัวแปรสุ่ม มักใช้ตัวอักษรภาษาอังกฤษตัวพิมพ์ใหญ่ ex.
ค่าของตัวแปรสุ่ม มักใช้ตัวอักษรภาษาอังกฤษตัวพิมพ์เล็ก ex.
Ex. ให้ เป็นตัวแปรสุ่มของจำนวนเหรียญที่ออกก้อยจากการโยนเหรียญ เหรียญ ครั้ง จะได้ว่า
โดยปกติแล้วจะใช้สัญลักษณ์ แทนเหตุการณ์ที่โยนเหรียญแล้วออกก้อย ครั้ง
และ แทนความน่าจะเป็นของเหตุการณ์ที่โยนเหรียญแล้วออกก้อย ครั้ง นั่นคือ
- คือ เหตุการณ์ที่โยนเหรียญแล้วออกก้อย ครั้ง (นั่นคือ โยนเหรียญแล้วได้เป็น )
และ แทนความน่าจะเป็นที่โยนเหรียญแล้วออกก้อย ครั้ง จะได้ว่า - คือ เหตุการณ์ที่โยนเหรียญแล้วออกก้อย ครั้ง (นั่นคือ โยนเหรียญแล้วได้เป็น และ )
และ แทนความน่าจะเป็นที่โยนเหรียญแล้วออกก้อย ครั้ง จะได้ว่า - คือ เหตุการณ์ที่โยนเหรียญแล้วออกก้อย ครั้ง (นั่นคือ โยนเหรียญแล้วได้เป็น )
และ แทนความน่าจะเป็นที่โยนเหรียญแล้วออกก้อย ครั้ง จะได้ว่า
นอกจากนี้ยังสามารถเขียนการแจกแจงความน่าจะเป็นได้ดังนี้
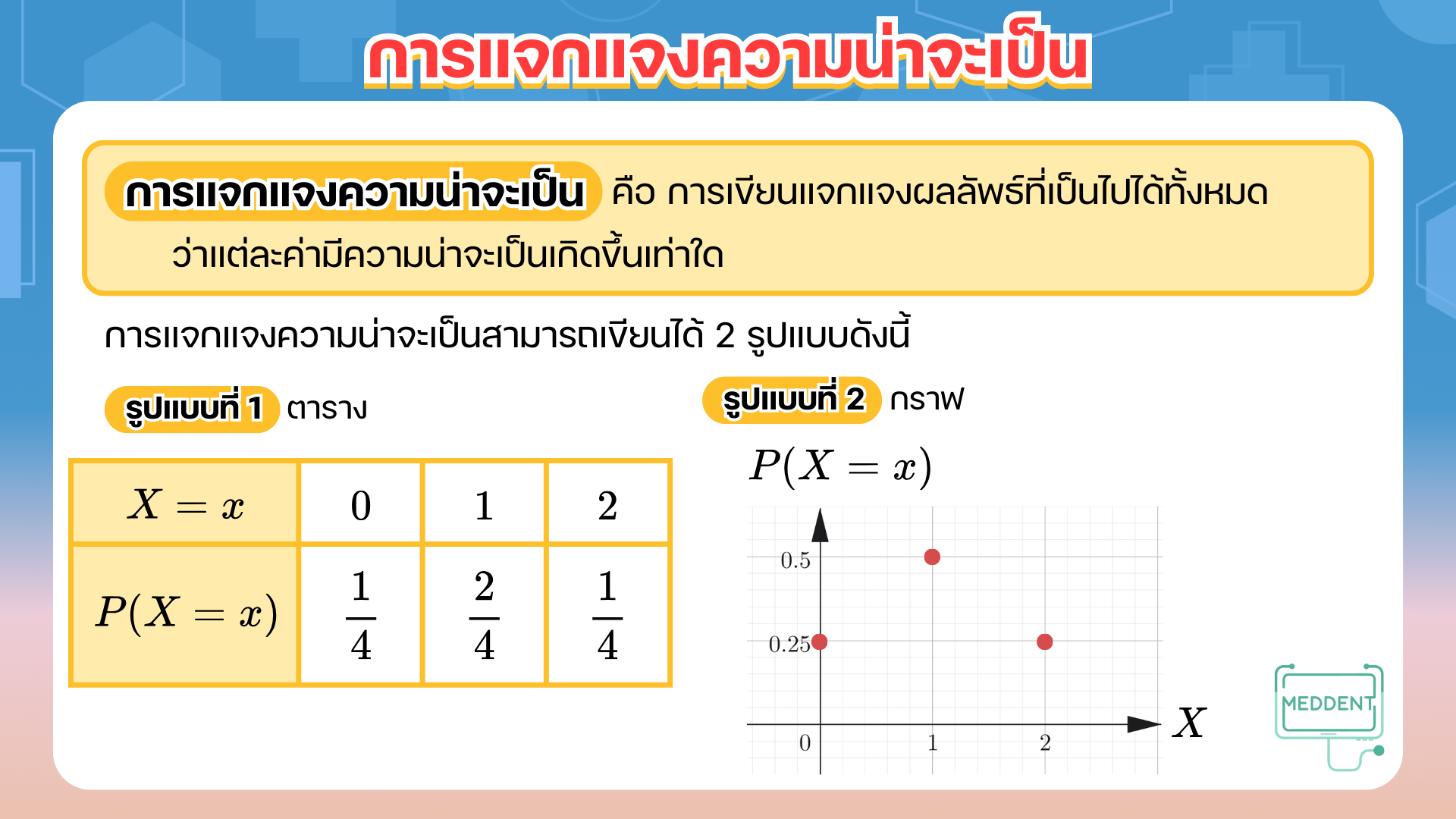
จากตัวอย่างข้างต้นจะเรียกตัวแปรสุ่ม ว่าตัวแปรสุ่มไม่ต่อเนื่อง
ต่อไปพี่แม็คจะให้น้อง ๆ มาทำความรู้จักกับตัวแปรสุ่มต่อเนื่องกันบ้าง ตามนี้เลยค้าบบ
Ex. ให้ เป็นตัวแปรสุ่มของคะแนนสอบของนักเรียนที่สอบในวิชาสถิติ ซึ่งสามารถเขียนการแจกแจงความน่าจะเป็นได้ดังนี้
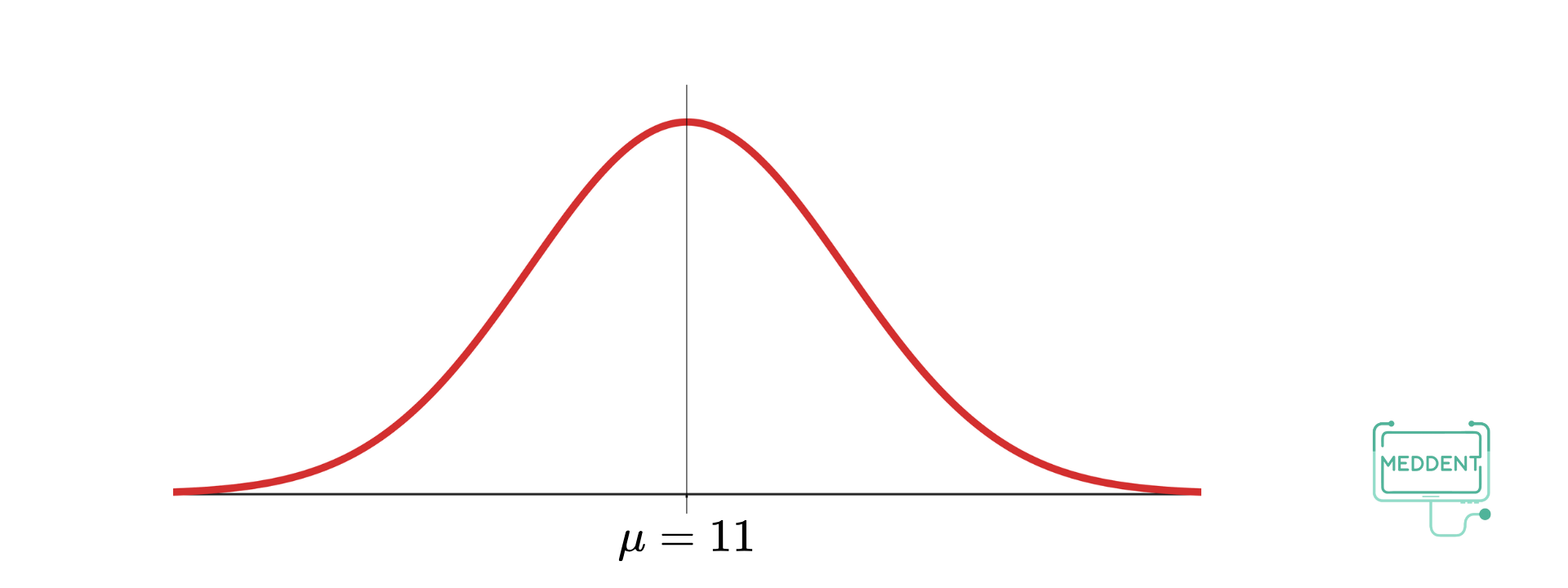
จะสังเกตเห็นว่า เส้นตรง จะเป็นเส้นตรงที่ผ่านจุดสูงสุดของกราฟและแบ่งกราฟออกเป็น ส่วนที่เท่ากัน ทำให้เส้นตรง เป็นแกนสมมาตรของกราฟนี้ เมื่อคำนวณหาค่าเฉลี่ยนเลขคณิตแล้ว ด้วยเช่นกัน จะเรียกการแจกแจงความน่าจะเป็นนี้ว่า การแจกแจงปกติ (normal distribution) และเรียกกราฟนี้ว่า เส้นโค้งปกติ
สำหรับการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม สามารถเขียนอยู่ในรูปของฟังก์ชันได้เป็น
ถ้าตัวแปรสุ่ม มีการแจกแจงปกติ จะเรียก ว่า ตัวแปรสุ่มปกติ
และสัญลักษณ์ เพื่อแสดงว่าเป็นการแจกแจงปกติ โดยเรียก ว่า พารามิเตอร์ของการแจกแจงปกติ
TIPS
- มีเส้นตั้งฉากกับแกน ที่ลากผ่านค่าเฉลี่ยเป็นแกนสมมาตร ทำให้พื้นที่ใต้เส้นโค้งทางด้านซ้าย ด้านขวา
- ปลายเส้นโค้งทั้งสองด้านเข้าใกล้แกน แต่จะไม่ตัดแกน
- ค่าเฉลี่ยเลขคณิต จะกำหนดลักษณะของเส้นโค้งว่ามีแกนสมมาตรอยู่ที่ใด
และส่วนเบี่ยงเบนมาตรฐาน จะกำหนดลักษณะของเส้นโค้งว่ามีการกระจายมากน้อยเพียงใด
Ex. ให้ เป็นตัวแปรสุ่มของคะแนนสอบของนักเรียนที่สอบในวิชาสถิติ ซึ่งเป็นการปรับค่าของตัวแปรสุ่ม ที่ทำให้ และ ดังนี้
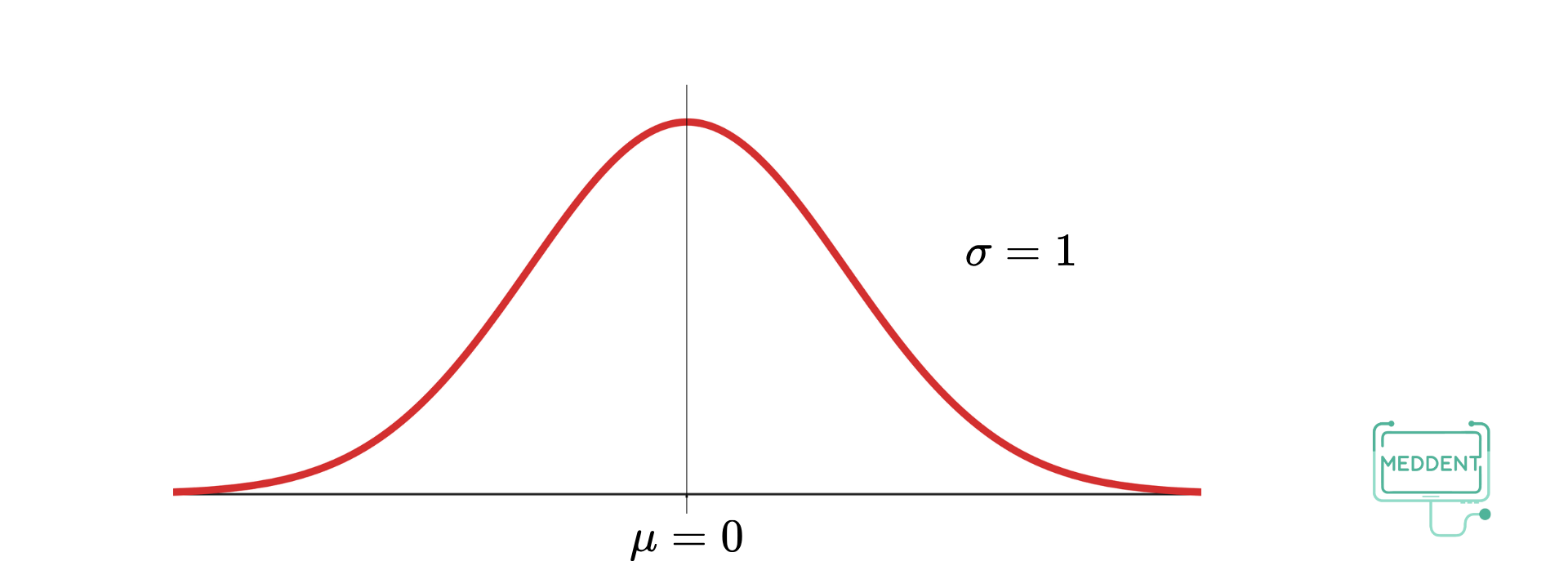
การแจกแจกความน่าจะเป็นในข้างต้นจะเรียกว่า การแจกแจกปกติมาตรฐาน และเรียกตัวแปรสุ่มที่มีการแจกแจงปกติมาตรฐานว่า ตัวแปรสุ่มปกติมาตรฐาน โดยทั่วไปนิยมใช้
ถ้า คือตัวแปรสุ่มปกติ แล้ว คือ ตัวแปรสุ่มปกติมาตรฐาน
โดยปกติแล้วถ้าน้อง ๆ ทราบว่าการแจกแจกความน่าจะเป็นใดเป็นการแจกแจงแบบปกติ จากข้อที่เป็นตัวแปรสุ่ม ที่เป็นตัวแปรสุ่มปกติ น้อง ๆ สามารถแปลงค่าให้ได้เป็นตัวแปรสุ่ม ได้ซึ่งเป็นตัวแปรสุ่มปกติมาตรฐาน แล้วทีนี้น้อง ๆ จะสามารถหาค่าความน่าจะเป็นที่จะเกิดเหตุการณ์ที่สนใจได้โดยการเปิดตารางค่า หรือตารางการแจกแจงปกติมาตรฐาน ดังนี้ค้าบบ
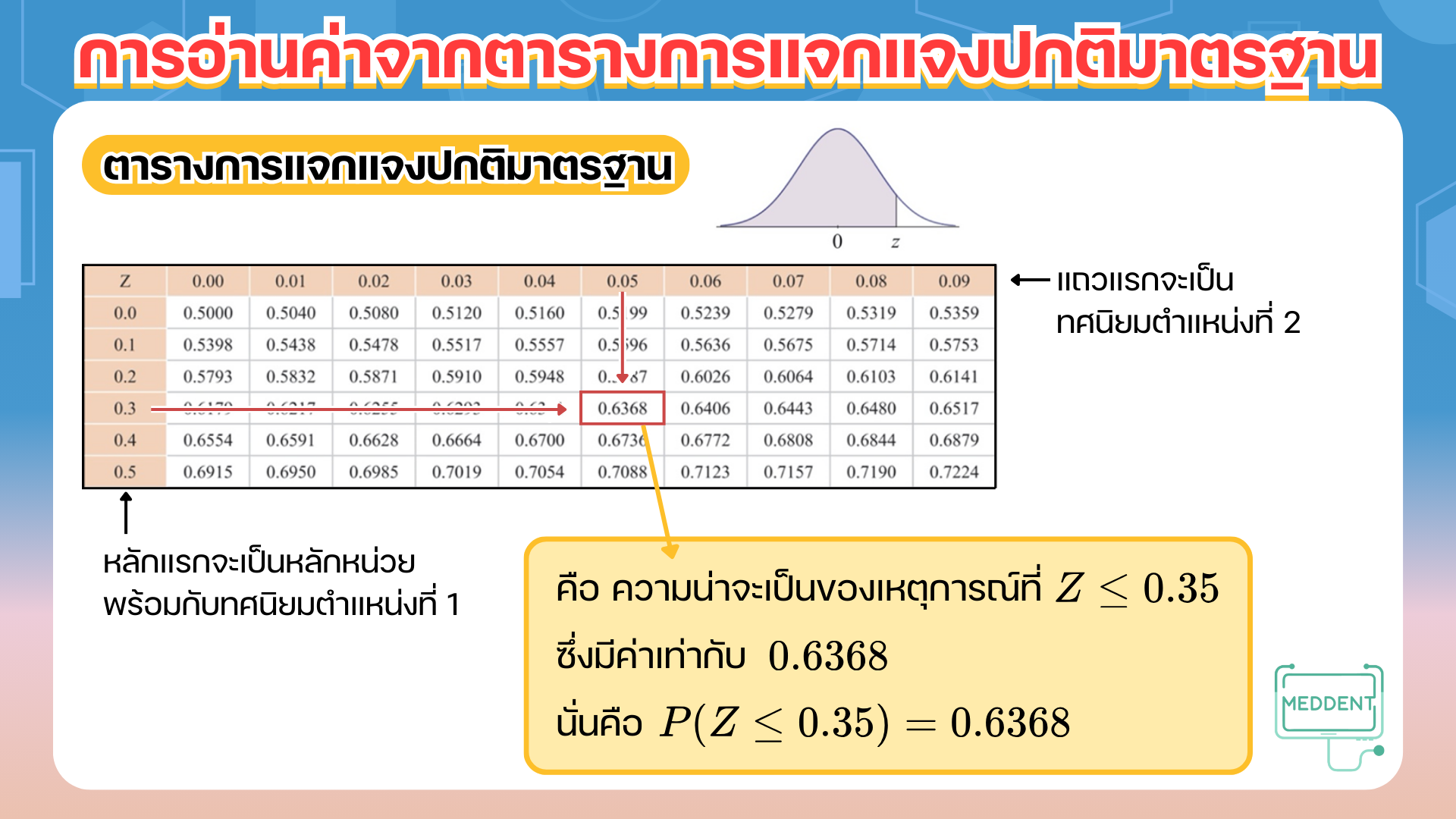
Ex. คะแนนสอบวิชาสถิติของนักเรียนห้องหนึ่งเป็นการแจกแจงแบบปกติ เมื่อหาค่าเฉลี่ยเลขคณิตได้ คะแนน และส่วนเบี่ยงเบนมาตรฐานเท่ากับ คะแนน เมื่อสุ่มนักเรียน คน จงหา
(1) ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนน
(2) ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนมากกว่าหรือเท่ากับ คะแนน
(3) ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนนหรือมากกว่า คะแนน
วิธีทำ เนื่องจากคะแนนสอบเป็นการแจกแจงแบบปกติ ดังนั้นในแต่ละข้อจะต้องปรับค่าก่อน
โดยใช้สูตร ก่อน เพื่อให้สามารถเปิดตารางแล้วหาความน่าจะเป็นต่อไปได้นั่นเองค้าบบ
กำหนดให้ เป็นตัวแปรสุ่มปกติซึ่งมี และ
และให้ เป็นตัวแปรสุ่มปกติมาตรฐาน
(1) เนื่องจากเหตุการณ์ที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนน คือ
เมื่อปรับค่าจะได้เป็นเหตุการณ์ที่
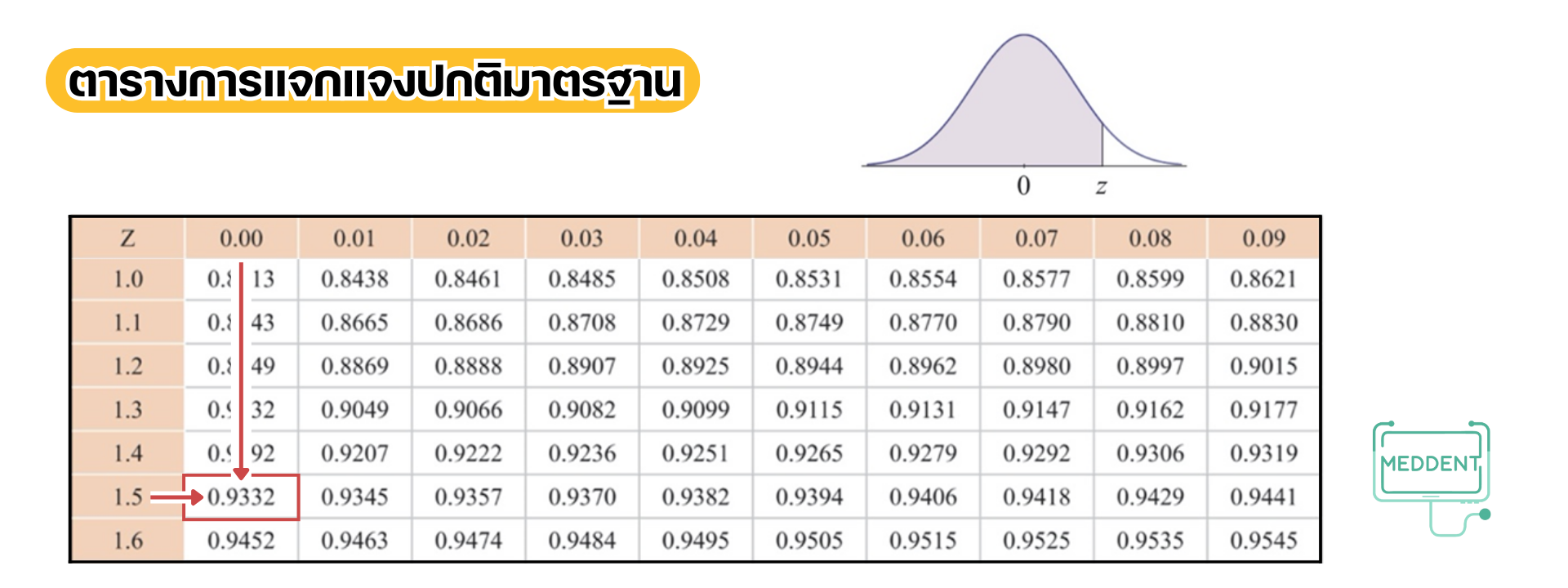
และดูค่าจากตารางแล้วพบว่า
ดังนั้น ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนน เท่ากับ
(2) เนื่องจากเหตุการณ์ที่นักเรียนคนนั้นได้คะแนนมากกว่าหรือเท่ากับ คะแนน คือ
เมื่อปรับค่าจะได้เป็นเหตุการณ์ที่
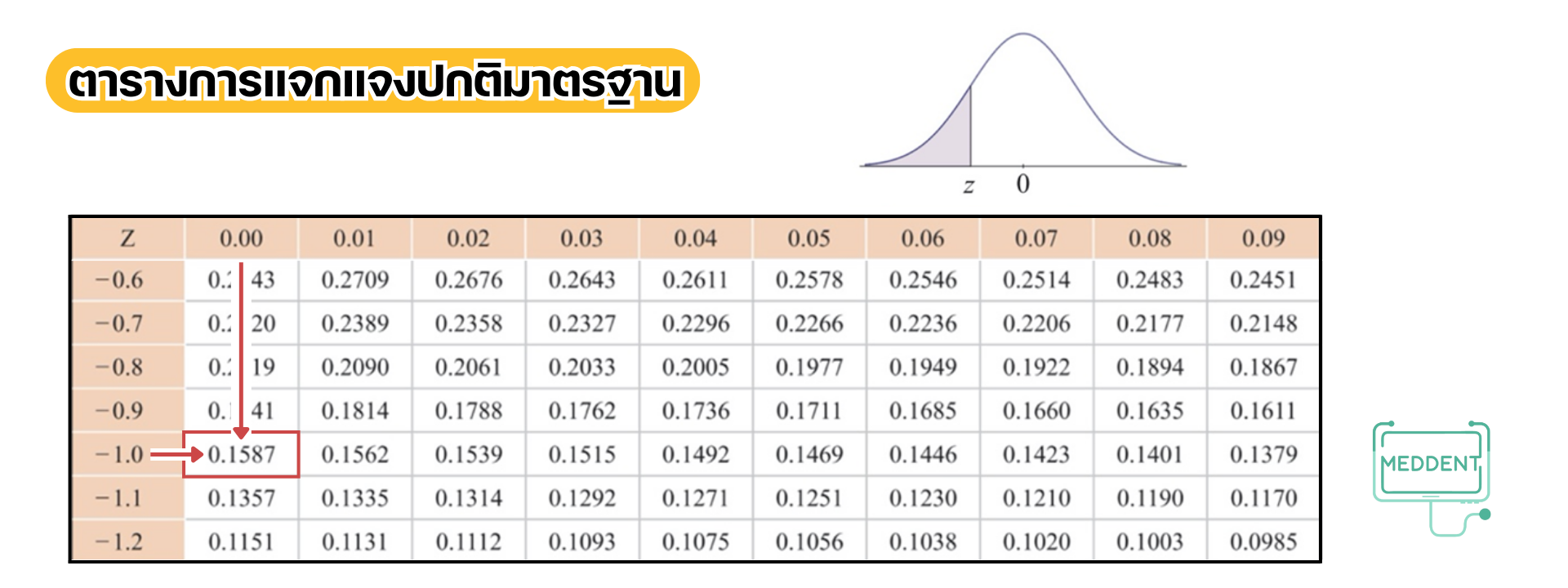
และดูค่าจากตารางแล้วพบว่า แต่เราต้องการหา
จากสมบัติความน่าจะเป็น ดังนั้นทำให้เราสามารถหา
ได้จาก
ดังนั้น ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนมากกว่าหรือเท่ากับ คะแนน เท่ากับ
จะสังเกตว่าความน่าจะเป็นนั่นคือเป็นการพิจารณาจากพื้นที่ใต้เส้นโค้งปกติกับแกน ซึ่งจะเห็นว่าพื้นที่จะนับเพียงแค่ส่วนที่เป็นบริเวณข้างในเท่านั้น ซึ่งจะไม่รวมกับเส้นขอบของพื้นที่ที่กำลังจะพิจารณาครับ
(3) เนื่องจากเหตุการณ์ที่ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนนหรือมากกว่า คะแนน คือ หรือ ซึ่งสามารถแบ่งกรณีคิดได้ดังนี้
สำหรับเหตุการณ์ เมื่อปรับค่าจะได้เป็นเหตุการณ์ที่
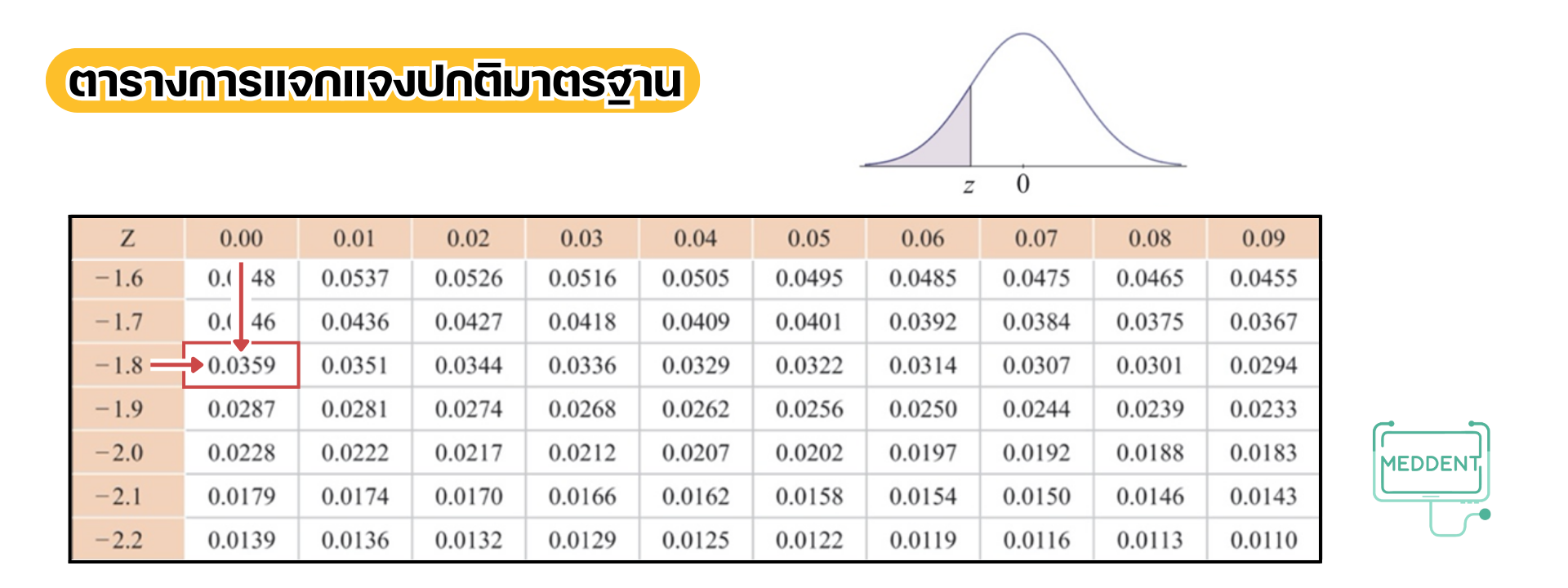
และดูค่าจากตารางแล้วพบว่า
และสำหรับเหตุการณ์ เมื่อปรับค่าจะได้เป็นเหตุการณ์ที่
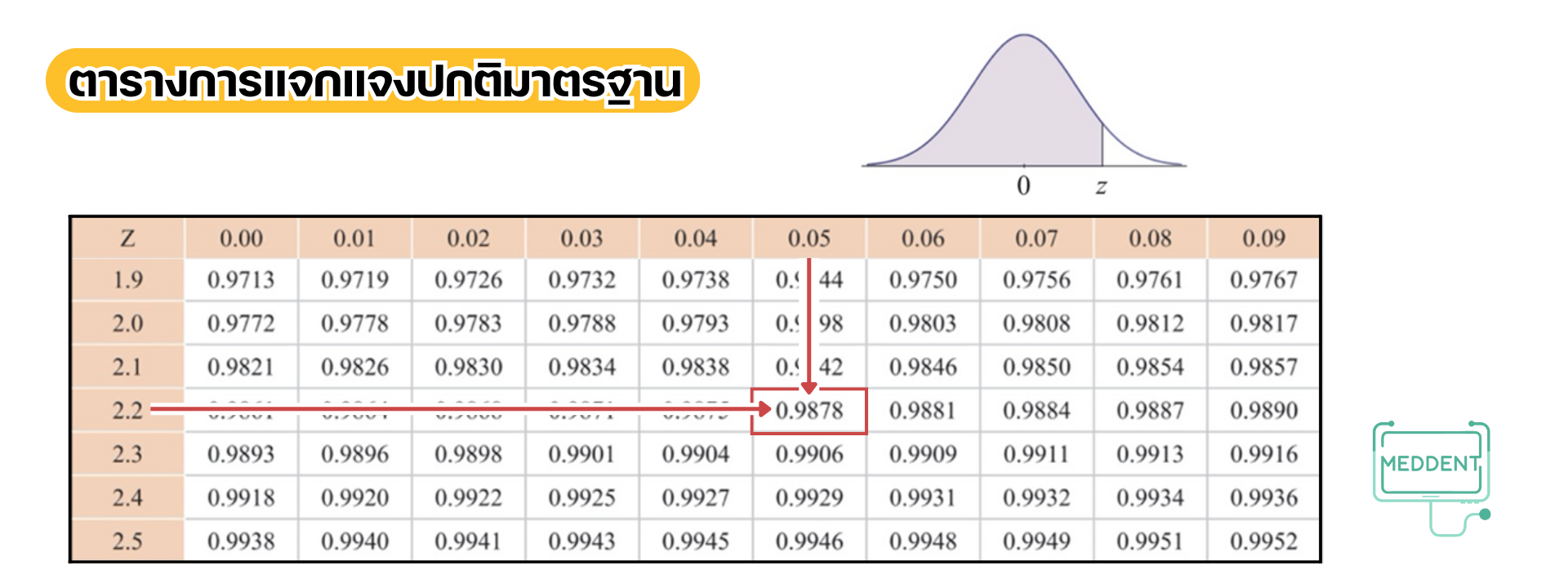
และดูค่าจากตารางแล้วพบว่า แต่เราต้องการหา
ดังนั้น
เนื่องจากเหตุการณ์ที่ และ ไม่เป็นเหตุการณ์ที่เกิดขึ้นร่วมกัน
จากสมบัติความน่าจะเป็น
ทำให้เราสามารถหาความน่าจะเป็นของทั้ง เหตุการณ์โดยนำความน่าจะเป็นของแต่ละเหตุการณ์มาบวกกัน
ดังนั้น ความน่าจะเป็นที่นักเรียนคนนั้นได้คะแนนน้อยกว่า คะแนนหรือมากกว่า คะแนน
เท่ากับ
ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1
เรื่องสถิติ (ปี 68)
ให้ เป็นข้อมูลชุดหนึ่งที่มีค่าเฉลี่ยเลขคณิตคือ
ถ้าตัด และ ออกไป จะทำให้ค่าเฉลี่ยเลขคณิตของข้อมูลชุดนี้เหลือ
ถ้าตัดเพียง ออกไป จะทำให้ค่าเฉลี่ยเลขคณิตของข้อมูลชุดนี้เหลือ
จงหาว่า มีค่าเท่ากับข้อใดต่อไปนี้
วิธีทำ เนื่องจาก จะได้ว่า
เนื่องจาก จะได้ว่า
นำสมการ (1) ลบกับสมการ (2) จะได้ว่า
เนื่องจาก จะได้ว่า
นำสมการ (1) ลบกับสมการ (3) จะได้ว่า
เนื่องจาก ดังนั้น
ดังนั้น
ตอบ ข้อ 3.

