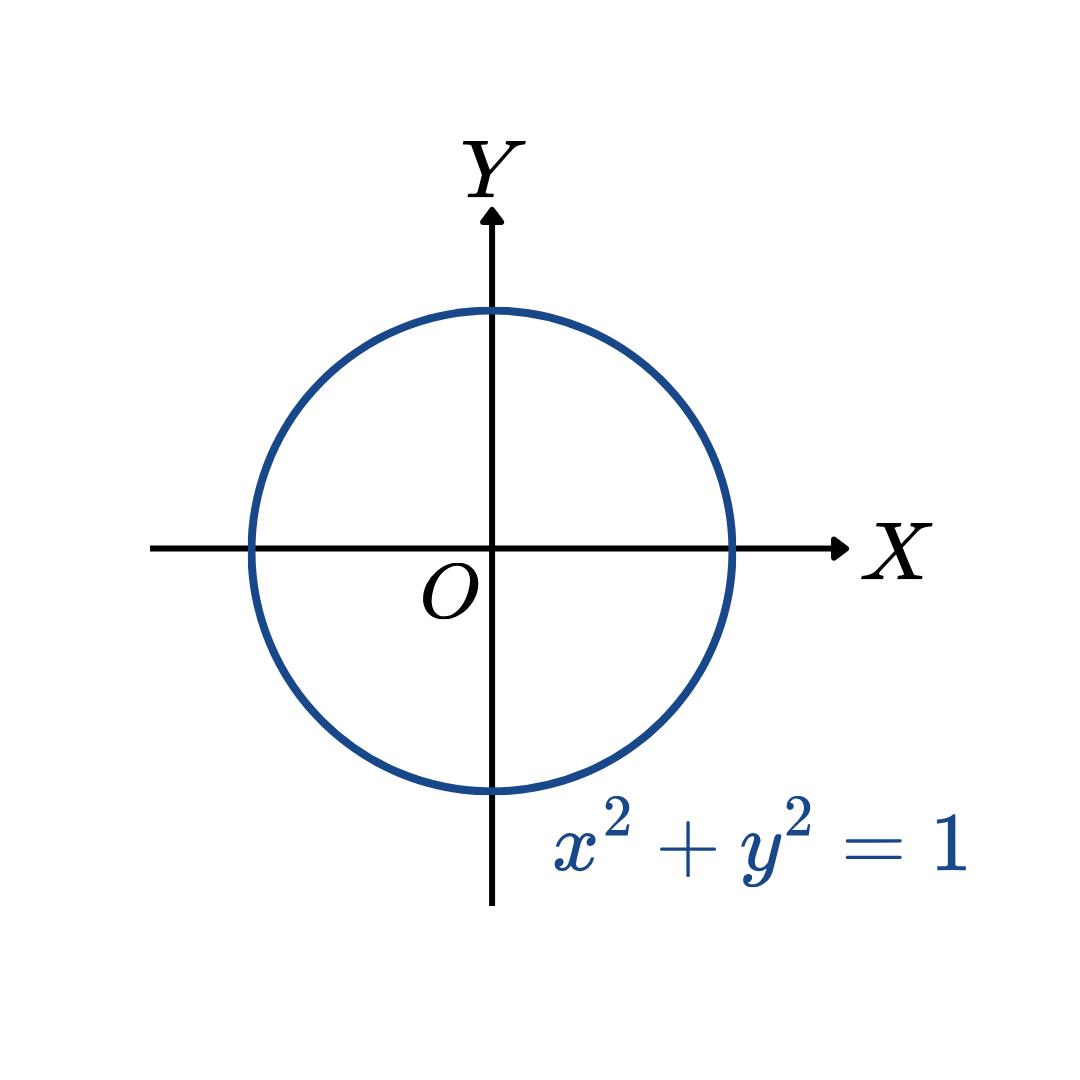สวัสดีน้อง ๆ ทุกคนนะค้าบบ ในตอนนี้พี่แม็คจะพูดถึงเกี่ยวกับฟังก์ชันตรีโกณมิติ ในตอนที่น้อง ๆ อยู่ม.ต้น น้อง ๆ ได้รู้จักเกี่ยวกับเรื่องอัตราส่วนตรีโกณมิติผ่านรูปสามเหลี่ยมมุมฉาก แต่ในระดับชั้น ม.ปลายนี้ น้อง ๆ จะรู้จักเกี่ยวกับฟังก์ชันตรีโกณมิติบนวงกลมหนึ่งหน่วย ซึ่งในตอนนี้พี่แม็คได้สรุปเกี่ยวกับฟังก์ชันตรีโกณมิติให้เข้าใจสั้น ๆ และง่าย ๆ ดังนี้ค้าบบ^^
วงกลมหนึ่งหน่วย คือ วงกลมที่มีรัศมี 1 1 1 ( 0 , 0 ) (0,0) ( 0 , 0 ) { ( x , y ) ∈ R × R ∣ x 2 + y 2 = 1 } \{ (x,y) \in \mathbb{R} \times \mathbb{R} | \ x^2 + y^2 = 1 \} {( x , y ) ∈ R × R ∣ x 2 + y 2 = 1 }
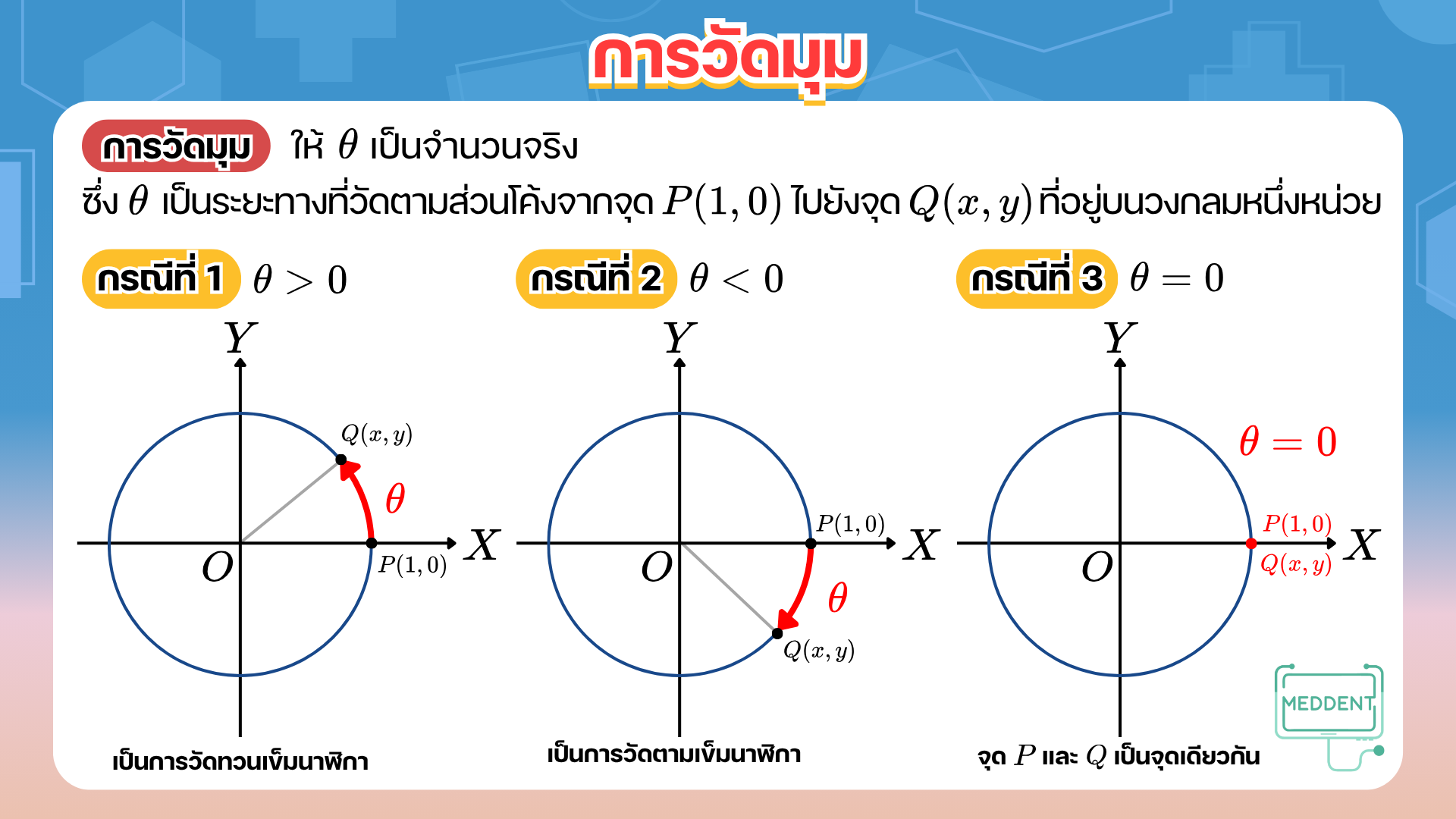
การวัดมุมเราจะกำหนดทิศทางการวัดมุมตามระยะทางที่เริ่มต้นจากจุด P ( 1 , 0 ) P(1,0) P ( 1 , 0 ) Q ( x , y ) Q(x,y) Q ( x , y ) 3 3 3
การวัดมุมในระดับชั้นม.ต้นที่น้อง ๆ รู้จักมา คือ องศา เขียนแทนด้วย ∘ ^\circ ∘ 360 ∘ 360^\circ 36 0 ∘ r r r 2 π r 2\pi r 2 π r 2 π r r = 2 π \displaystyle\frac{2\pi r}{r} = 2\pi r 2 π r = 2 π
การแปลงหน่วยดีกรีเป็นหน่วยเรเดียน เนื่องจาก 180 180 180 π \pi π ถ้ามุม x x x x ( π 180 ) x \left(\displaystyle\frac{\pi}{180}\right) x ( 180 π )
Ex. มุม 60 ∘ 60^\circ 6 0 ∘ วิธีทำ มุม 60 ∘ 60^\circ 6 0 ∘ 60 ( π 180 ) = π 3 60 \left(\displaystyle\frac{\pi}{180}\right) = \displaystyle\frac{\pi}{3} 60 ( 180 π ) = 3 π
Ex. มุม 315 ∘ 315^\circ 31 5 ∘ วิธีทำ มุม 315 ∘ 315^\circ 31 5 ∘ 315 ( π 180 ) = 7 π 4 315 \left(\displaystyle\frac{\pi}{180}\right) = \displaystyle\frac{7\pi}{4} 315 ( 180 π ) = 4 7 π
การแปลงหน่วยเรเดียนเป็นหน่วยดีกรี เนื่องจาก π \pi π 180 180 180 ถ้ามุม x x x x ( 180 π ) x \left(\displaystyle\frac{180}{\pi}\right) x ( π 180 )
Ex. มุม π 12 \displaystyle\frac{\pi}{12} 12 π วิธีทำ มุม π 12 \displaystyle\frac{\pi}{12} 12 π π 12 ( 180 π ) = 15 \displaystyle\frac{\pi}{12} \left(\displaystyle\frac{180}{\pi}\right) = 15 12 π ( π 180 ) = 15
Ex. มุม 7 π 6 \displaystyle\frac{7\pi}{6} 6 7 π วิธีทำ มุม 7 π 6 \displaystyle\frac{7\pi}{6} 6 7 π 7 π 6 ( 180 π ) = 210 \displaystyle\frac{7\pi}{6} \left(\displaystyle\frac{180}{\pi}\right) = 210 6 7 π ( π 180 ) = 210
ซึ่งพี่แม็คได้สรุปความสัมพันธ์การวัดมุมหน่วยดีกรีและหน่วยเรเดียนของมุมต่าง ๆ ดังนี้
ตารางแสดงความสัมพันธ์การวัดมุมหน่วยดีกรีและหน่วยเรเดียน
มุมในหน่วยดีกรี 360 ∘ 180 ∘ 90 ∘ 60 ∘ 45 ∘ 30 ∘ 0 ∘ มุมในหน่วยเรเดียน 2 π π π 2 π 3 π 4 π 6 0 \displaystyle \begin{array} {|c|c|c|c|c|c|c|c|} \hline \\ \textbf{มุมในหน่วยดีกรี} & 360^\circ & 180^\circ & 90^\circ & 60^\circ & 45^\circ & 30^\circ & 0^\circ \\ \hline \\ \textbf{มุมในหน่วยเรเดียน} & 2\pi & \pi & \frac{\pi}{2} & \frac{\pi}{3} & \frac{\pi}{4} & \frac{\pi}{6} & 0 \\ \\ \hline \end{array} มุมในหน่วยดีกรี มุมในหน่วยเรเดียน 36 0 ∘ 2 π 18 0 ∘ π 9 0 ∘ 2 π 6 0 ∘ 3 π 4 5 ∘ 4 π 3 0 ∘ 6 π 0 ∘ 0
ในหัวข้อนี้พี่แม็คจะให้น้อง ๆ ทำความรู้จักกับฟังก์ชันตรีโกณมิติ ได้แก่ ฟังก์ชันไซน์ (sine function: sin \sin sin cos \cos cos tan \tan tan c o s e c \mathrm{cosec} cosec csc \csc csc sec \sec sec cot \cot cot
จากภาพจะเห็นว่า จำนวนจริง θ \theta θ R \mathbb{R} R ( x , y ) (x,y) ( x , y ) − 1 ≤ x ≤ 1 -1 \leq x \leq 1 − 1 ≤ x ≤ 1 − 1 ≤ y ≤ 1 -1 \leq y \leq 1 − 1 ≤ y ≤ 1 [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ]
ข้อสังเกต (1) D sin = R D_{\sin} = \mathbb{R} D s i n = R D cos = R D_{\cos} = \mathbb{R} D c o s = R (2) R sin = [ − 1 , 1 ] R_{\sin} = [-1, 1] R s i n = [ − 1 , 1 ] R cos = [ − 1 , 1 ] R_{\cos} = [-1, 1] R c o s = [ − 1 , 1 ]
ฟังก์ชันตรีโกณมิติอื่น ๆ ได้แก่ ฟังก์ชันแทนเจนต์ ฟังก์ชันโคเซแคนต์ ฟังก์ชันเซแคนต์ ฟังก์ชันโคแทนเจนต์ จะนิยามผ่านฟังก์ชันไซน์และฟังก์ชันโคไซน์ ดังนี้
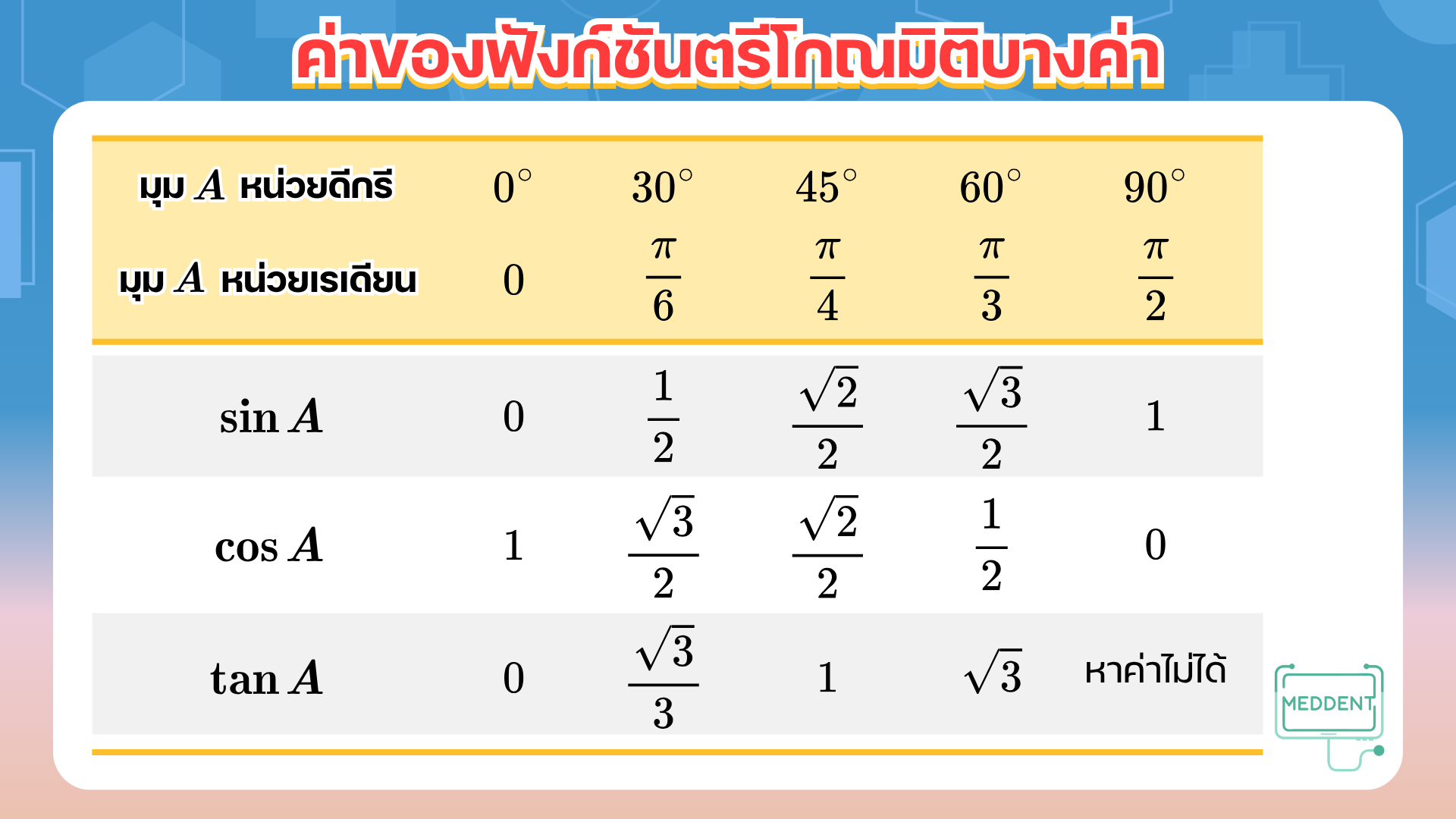
ซึ่งพี่แม็คได้หาค่าของฟังก์ชันตรีโกณมิติสำหรับบางค่าที่อยู่ในช่วง [ 0 , π 2 ] \left[0, \displaystyle\frac{\pi}{2}\right] [ 0 , 2 π ]
จากสมการวงกลม x 2 + y 2 = 1 x^2 + y^2 = 1 x 2 + y 2 = 1 cos 2 θ + sin 2 θ = 1 \cos^2\theta + \sin^2\theta = 1 cos 2 θ + sin 2 θ = 1
ถ้านำ cos 2 θ \cos^2\theta cos 2 θ cos 2 θ + sin 2 θ = 1 \cos^2\theta + \sin^2\theta = 1 cos 2 θ + sin 2 θ = 1 จะได้ 1 + sin 2 θ cos 2 θ = 1 cos 2 θ \displaystyle 1 + \frac{\sin^2\theta}{\cos^2\theta} = \frac{1}{\cos^2\theta} 1 + cos 2 θ sin 2 θ = cos 2 θ 1 1 + tan 2 θ = sec 2 θ 1 + \tan^2\theta = \sec^2\theta 1 + tan 2 θ = sec 2 θ
และนำ sin 2 θ \sin^2\theta sin 2 θ cos 2 θ + sin 2 θ = 1 \cos^2\theta + \sin^2\theta = 1 cos 2 θ + sin 2 θ = 1 จะได้ cos 2 θ sin 2 θ + 1 = 1 sin 2 θ \displaystyle \frac{\cos^2\theta}{\sin^2\theta} + 1 = \frac{1}{\sin^2\theta} sin 2 θ cos 2 θ + 1 = sin 2 θ 1 cot 2 θ + 1 = c o s e c 2 θ \cot^2\theta + 1 = \mathrm{cosec}^2\theta cot 2 θ + 1 = cosec 2 θ
สรุปเอกลักษณ์ตรีโกณมิติ
cos 2 θ + sin 2 θ = 1 \cos^2\theta + \sin^2\theta = 1 cos 2 θ + sin 2 θ = 1 1 + tan 2 θ = sec 2 θ 1 + \tan^2\theta = \sec^2\theta 1 + tan 2 θ = sec 2 θ 1 + cot 2 θ = c o s e c 2 θ 1 + \cot^2\theta = \mathrm{cosec}^2\theta 1 + cot 2 θ = cosec 2 θ เอกลักษณ์ตรีโกณมิติของผลบวกมุมและผลต่างมุม
cos ( α − β ) = cos α cos β + sin α sin β \cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta cos ( α − β ) = cos α cos β + sin α sin β cos ( α + β ) = cos α cos β − sin α sin β \cos(\alpha + \beta) = \cos\alpha \cos\beta - \sin\alpha \sin\beta cos ( α + β ) = cos α cos β − sin α sin β sin ( α − β ) = sin α cos β − cos α sin β \sin(\alpha - \beta) = \sin\alpha \cos\beta - \cos\alpha \sin\beta sin ( α − β ) = sin α cos β − cos α sin β sin ( α + β ) = sin α cos β + cos α sin β \sin(\alpha + \beta) = \sin\alpha \cos\beta + \cos\alpha \sin\beta sin ( α + β ) = sin α cos β + cos α sin β tan ( α − β ) = tan α − tan β 1 + tan α tan β เมื่อ tan α tan β ≠ − 1 \tan(\alpha - \beta) = \displaystyle\frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \quad \text{เมื่อ } \tan \alpha \tan \beta \neq -1 tan ( α − β ) = 1 + tan α tan β tan α − tan β เมื่อ tan α tan β = − 1 tan ( α + β ) = tan α + tan β 1 − tan α tan β เมื่อ tan α tan β ≠ 1 \tan(\alpha + \beta) = \displaystyle\frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \quad \text{เมื่อ } \tan \alpha \tan \beta \neq 1 tan ( α + β ) = 1 − tan α tan β tan α + tan β เมื่อ tan α tan β = 1 2 sin α cos β = sin ( α + β ) + sin ( α − β ) 2\sin \alpha \cos \beta = \sin(\alpha + \beta) + \sin(\alpha - \beta) 2 sin α cos β = sin ( α + β ) + sin ( α − β ) 2 cos α sin β = sin ( α + β ) − sin ( α − β ) 2\cos \alpha \sin \beta = \sin(\alpha + \beta) - \sin(\alpha - \beta) 2 cos α sin β = sin ( α + β ) − sin ( α − β ) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2\cos \alpha \cos \beta = \cos(\alpha + \beta) + \cos(\alpha - \beta) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2 sin α sin β = cos ( α − β ) − cos ( α + β ) 2\sin \alpha \sin \beta = \cos(\alpha - \beta) - \cos(\alpha + \beta) 2 sin α sin β = cos ( α − β ) − cos ( α + β ) sin α + sin β = 2 sin α + β 2 cos α − β 2 \sin \alpha + \sin \beta = 2\sin \displaystyle\frac{\alpha + \beta}{2} \cos \displaystyle\frac{\alpha - \beta}{2} sin α + sin β = 2 sin 2 α + β cos 2 α − β sin α − sin β = 2 cos α + β 2 sin α − β 2 \sin \alpha - \sin \beta = 2\cos \displaystyle\frac{\alpha + \beta}{2} \sin \displaystyle\frac{\alpha - \beta}{2} sin α − sin β = 2 cos 2 α + β sin 2 α − β cos α + cos β = 2 cos α + β 2 cos α − β 2 \cos \alpha + \cos \beta = 2\cos \displaystyle\frac{\alpha + \beta}{2} \cos \displaystyle\frac{\alpha - \beta}{2} cos α + cos β = 2 cos 2 α + β cos 2 α − β cos α − cos β = − 2 sin α + β 2 sin α − β 2 \cos \alpha - \cos \beta = -2\sin \displaystyle\frac{\alpha + \beta}{2} \sin \displaystyle\frac{\alpha - \beta}{2} cos α − cos β = − 2 sin 2 α + β sin 2 α − β เอกลักษณ์ตรีโกณมิติของมุมสองเท่า
sin 2 α = 2 sin α cos α \sin 2\alpha = 2\sin \alpha \cos \alpha sin 2 α = 2 sin α cos α cos 2 α = cos 2 α − sin 2 α \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha cos 2 α = cos 2 α − sin 2 α cos 2 α = 1 − 2 sin 2 α \cos 2\alpha = 1 - 2\sin^2 \alpha cos 2 α = 1 − 2 sin 2 α cos 2 α = 2 cos 2 α − 1 \cos 2\alpha = 2\cos^2 \alpha - 1 cos 2 α = 2 cos 2 α − 1 tan 2 α = 2 tan α 1 − tan 2 α เมื่อ tan 2 α ≠ 1 \tan 2\alpha = \displaystyle\frac{2 \tan \alpha}{1 - \tan^2 \alpha} \quad \text{เมื่อ } \tan^2 \alpha \neq 1 tan 2 α = 1 − tan 2 α 2 tan α เมื่อ tan 2 α = 1 Ex. จงแสดงว่า 1 + sin θ 1 − sin θ = c o s e c θ + 1 c o s e c θ − 1 \displaystyle\frac{1 + \sin \theta}{1 - \sin \theta} = \displaystyle\frac{\mathrm{cosec} \theta + 1}{\mathrm{cosec} \theta - 1} 1 − sin θ 1 + sin θ = cosec θ − 1 cosec θ + 1 วิธีทำ เนื่องจาก c o s e c θ = 1 sin θ \mathrm{cosec} \theta = \displaystyle\frac{1}{\sin \theta} cosec θ = sin θ 1
c o s e c θ + 1 c o s e c θ − 1 = 1 sin θ + 1 1 sin θ − 1 = 1 + sin θ sin θ 1 − sin θ sin θ = 1 + sin θ sin θ × sin θ 1 − sin θ = 1 + sin θ 1 − sin θ \begin{align*} \displaystyle\frac{\mathrm{cosec} \theta + 1}{\mathrm{cosec} \theta - 1} &= \displaystyle\frac{\displaystyle\frac{1}{\sin \theta} + 1}{\displaystyle\frac{1}{\sin \theta} - 1} \\ \\ &= \displaystyle\frac{\displaystyle\frac{1 + \sin \theta}{\sin \theta}}{\displaystyle\frac{1 - \sin \theta}{\sin \theta}} \\ \\ &= \displaystyle\frac{1 + \sin \theta}{\sin \theta} \times \displaystyle\frac{\sin \theta}{1 - \sin \theta} \\ \\ &= \displaystyle\frac{1 + \sin \theta}{1 - \sin \theta} \end{align*} cosec θ − 1 cosec θ + 1 = sin θ 1 − 1 sin θ 1 + 1 = sin θ 1 − sin θ sin θ 1 + sin θ = sin θ 1 + sin θ × 1 − sin θ sin θ = 1 − sin θ 1 + sin θ
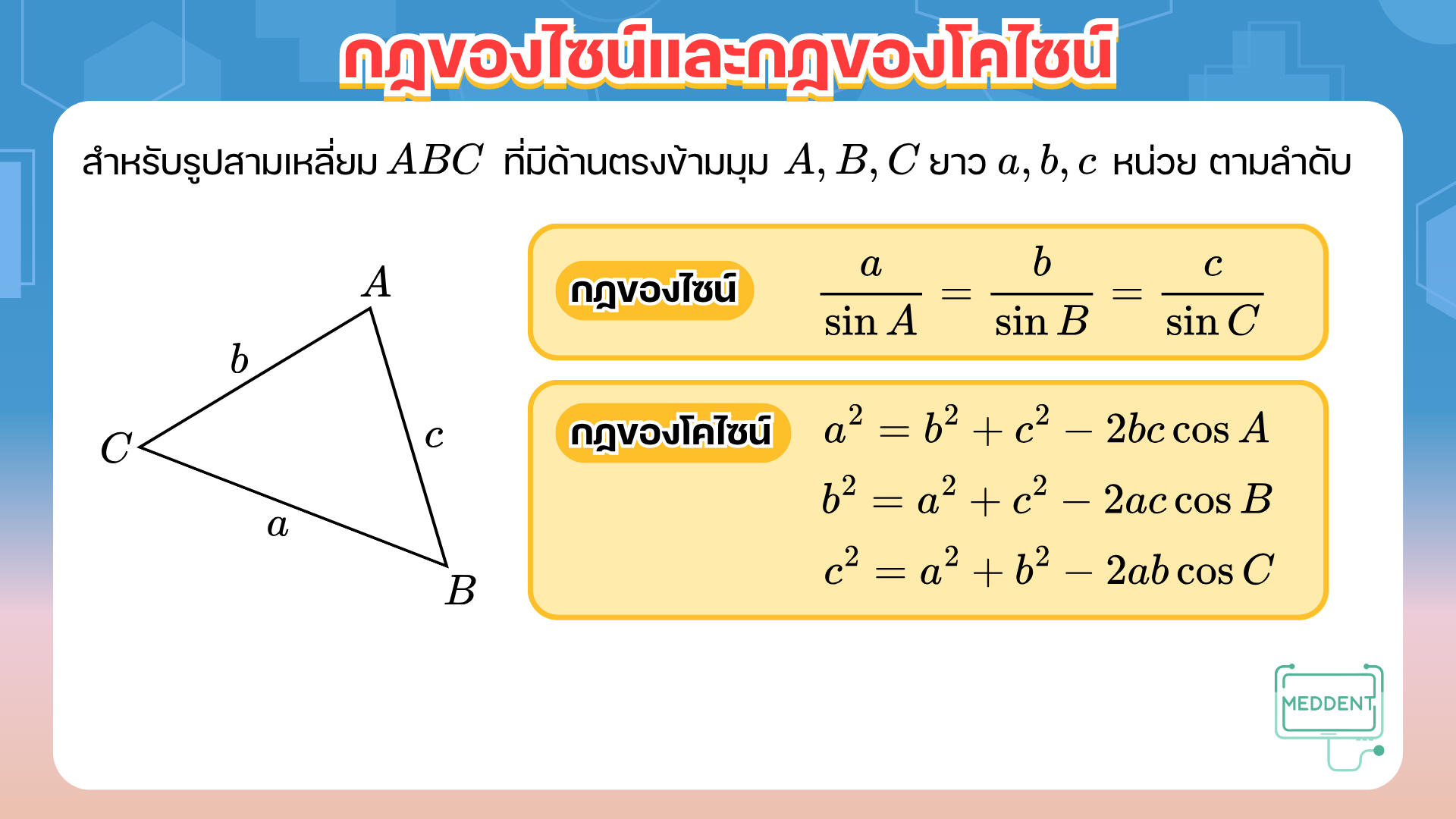
Ex. กำหนดรูปสามเหลี่ยม A B C ABC A BC B C BC BC 21 21 21 A A A B B B 30 30 30 105 105 105 A B AB A B วิธีทำ ก่อนอื่นจะหามุม C C C เนื่องจากมุม A A A B B B 30 30 30 105 105 105 แสดงว่ามุม C C C 180 ∘ − 30 ∘ − 105 ∘ = 45 ∘ 180^\circ-30^\circ-105^\circ = 45^\circ 18 0 ∘ − 3 0 ∘ − 10 5 ∘ = 4 5 ∘ จากกฎของไซน์ B C sin A = A B sin C \displaystyle\frac{BC}{\sin{A}} = \displaystyle\frac{AB}{\sin{C}} sin A BC = sin C A B 20 sin 30 ∘ = A B sin 45 ∘ \displaystyle\frac{20}{\sin{30^\circ}} = \displaystyle\frac{AB}{\sin{45^\circ}} sin 3 0 ∘ 20 = sin 4 5 ∘ A B นั่นคือ A B = 21 sin 30 ∘ × sin 45 ∘ = 21 1 2 × 2 2 = 21 2 AB = \displaystyle\frac{21}{\sin{30^\circ}} \times \sin{45^\circ} = \displaystyle\frac{21}{\displaystyle\frac{1}{2}} \times \displaystyle\frac{\sqrt{2}}{2} = 21\sqrt{2} A B = sin 3 0 ∘ 21 × sin 4 5 ∘ = 2 1 21 × 2 2 = 21 2
Ex. กำหนดรูปสามเหลี่ยม X Y Z XYZ X Y Z Y Z YZ Y Z X Z XZ XZ 4 4 4 4 3 4\sqrt{3} 4 3 Z Z Z 30 30 30 X Y XY X Y วิธีทำ ให้ x , y x, y x , y z z z Y Z , X Z YZ, XZ Y Z , XZ X Y XY X Y x = 4 x=4 x = 4 y = 4 3 y=4\sqrt{3} y = 4 3 จากกฎของโคไซน์ z 2 = x 2 + y 2 − 2 x y cos Z z^2 = x^2 + y^2 - 2xy\cos{Z} z 2 = x 2 + y 2 − 2 x y cos Z จะได้ว่า z 2 = 4 2 + ( 4 3 ) 2 − 2 ( 4 ) ( 4 3 ) cos 30 ∘ = 16 + 48 − 32 3 ( 3 2 ) = 64 − 16 ⋅ 3 = 16 z^2 = 4^2 + (4\sqrt{3})^2 - 2(4)(4\sqrt{3})\cos{30^\circ} = 16 + 48 - 32\sqrt{3} \left(\displaystyle\frac{\sqrt{3}}{2}\right) = 64 - 16 \cdot 3 = 16 z 2 = 4 2 + ( 4 3 ) 2 − 2 ( 4 ) ( 4 3 ) cos 3 0 ∘ = 16 + 48 − 32 3 ( 2 3 ) = 64 − 16 ⋅ 3 = 16 z = 4 z = 4 z = 4
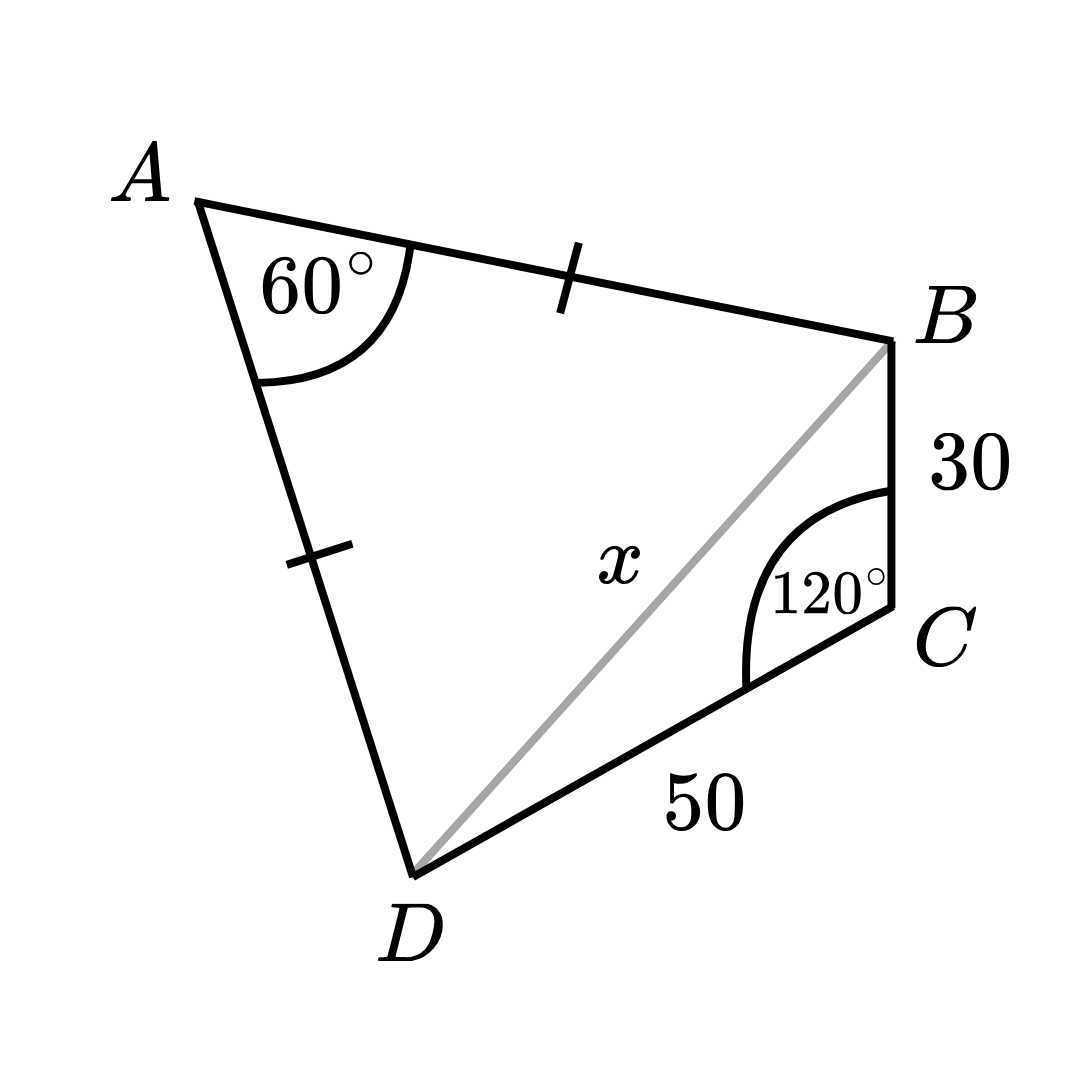
รูปสี่เหลี่ยม A B C D ABCD A BC D A A A 60 60 60 A A A มุม C C C A A A 120 120 120 C C C 30 30 30 50 50 50 จงหาว่า ด้าน A B AB A B
80 80 80 70 70 70 60 60 60 50 50 50 40 40 40 วิธีทำ
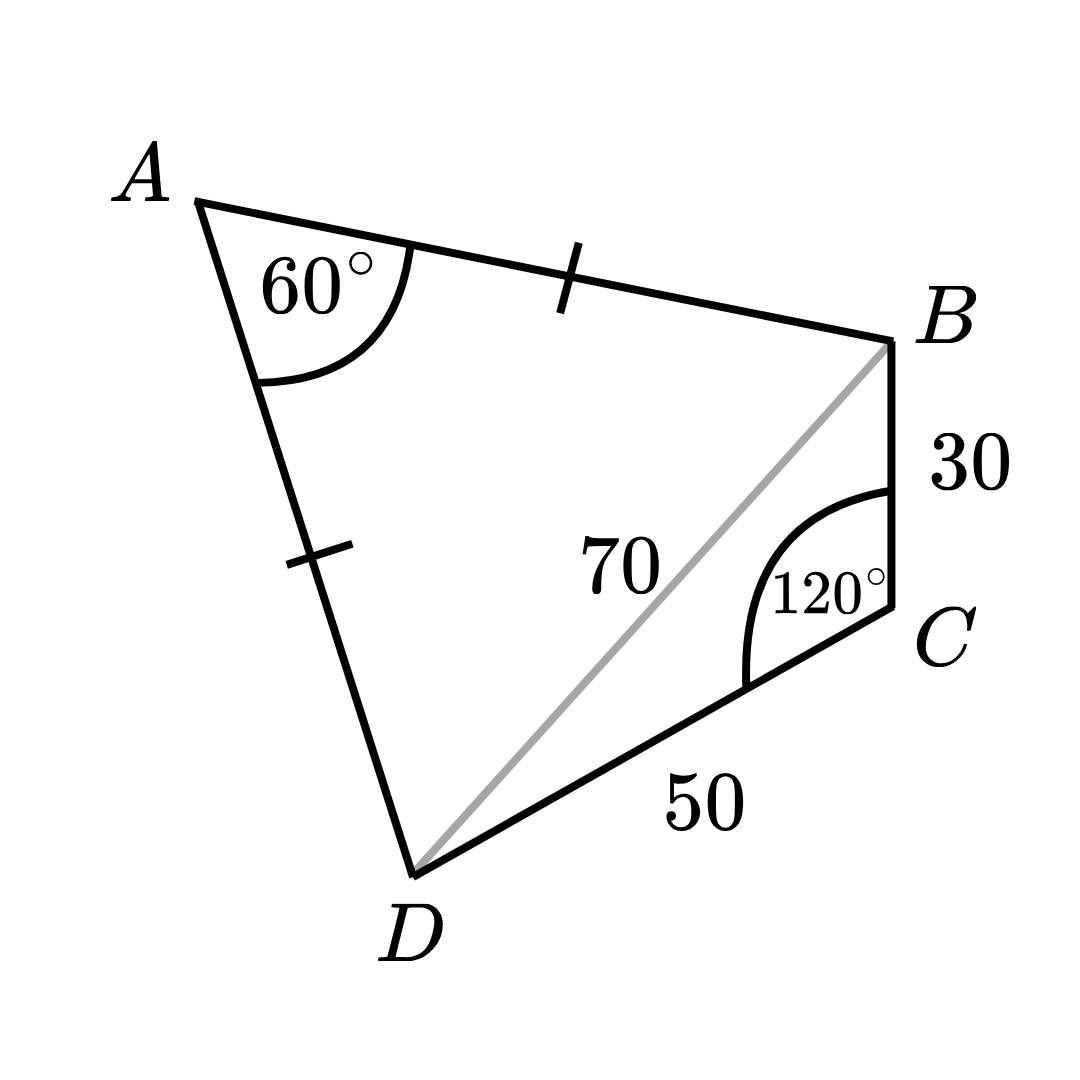
ให้ x x x B D BD B D A B C D ABCD A BC D โดยกฎของโคไซน์ จะได้ว่า x 2 = ( 30 ) 2 + ( 50 ) 2 − 2 ( 30 ) ( 50 ) cos C = x 2 = 900 + 2500 − 3000 cos 120 ∘ x^2 = (30)^2 + (50)^2 - 2(30)(50)\cos{C} = x^2 = 900 + 2500 - 3000 \cos{120^\circ} x 2 = ( 30 ) 2 + ( 50 ) 2 − 2 ( 30 ) ( 50 ) cos C = x 2 = 900 + 2500 − 3000 cos 12 0 ∘ จากเอกลักษณ์ตรีโกณมิติของมุมสองเท่า cos 2 α = 2 cos 2 α − 1 \cos 2\alpha = 2\cos^2 \alpha - 1 cos 2 α = 2 cos 2 α − 1 จะได้ว่า cos 120 ∘ = cos ( 2 ⋅ 60 ∘ ) = 2 cos 2 ( 60 ∘ ) − 1 = 2 ( 1 2 ) 2 − 1 = − 1 2 \cos{120^\circ} = \cos{(2 \cdot 60^\circ)} = 2\cos^2 {(60^\circ)} - 1 = 2\left(\displaystyle\frac{1}{2}\right)^2 - 1 = -\displaystyle\frac{1}{2} cos 12 0 ∘ = cos ( 2 ⋅ 6 0 ∘ ) = 2 cos 2 ( 6 0 ∘ ) − 1 = 2 ( 2 1 ) 2 − 1 = − 2 1 ดังนั้น x 2 = 900 + 2500 − 3000 ( − 1 2 ) = 4900 x^2 = 900 + 2500 - 3000 \left(-\displaystyle\frac{1}{2}\right) = 4900 x 2 = 900 + 2500 − 3000 ( − 2 1 ) = 4900 เพราะฉะนั้น x = 70 x = 70 x = 70
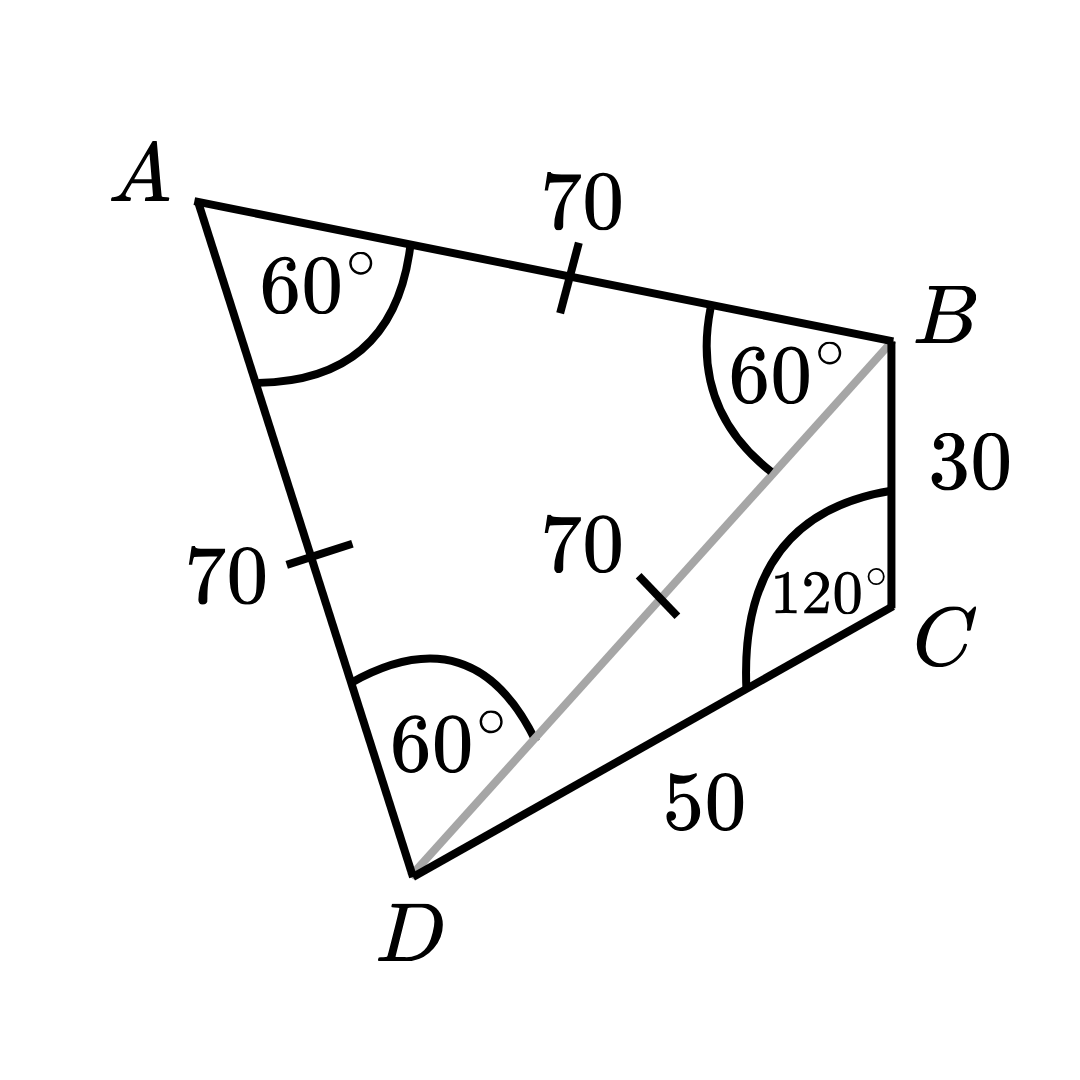
เนื่องจากด้านประกอบมุม A A A A B D ABD A B D A A A A B D ABD A B D A B ^ D = A D ^ B A\hat{B}D = A\hat{D}B A B ^ D = A D ^ B เนื่องจากมุมภายในของรูปสามเหลี่ยมเท่ากับ 180 ∘ 180^\circ 18 0 ∘ B A ^ D + A B ^ D + A D ^ B = 180 ∘ B\hat{A}D + A\hat{B}D + A\hat{D}B = 180^\circ B A ^ D + A B ^ D + A D ^ B = 18 0 ∘ ทำให้ได้ว่า 60 ∘ + 2 ( A B ^ D ) = 180 ∘ 60^\circ + 2(A\hat{B}D) = 180^\circ 6 0 ∘ + 2 ( A B ^ D ) = 18 0 ∘ A B ^ D = 180 ∘ − 60 ∘ 2 = 120 ∘ 2 = 60 ∘ A\hat{B}D = \displaystyle\frac{180^\circ-60^\circ}{2} = \displaystyle\frac{120^\circ}{2} = 60^\circ A B ^ D = 2 18 0 ∘ − 6 0 ∘ = 2 12 0 ∘ = 6 0 ∘ ดังนั้น A B ^ D = A D ^ B = 60 ∘ A\hat{B}D = A\hat{D}B = 60^\circ A B ^ D = A D ^ B = 6 0 ∘
เห็นว่ามุมทุกมุมของรูปสามเหลี่ยม A B D ABD A B D A B D ABD A B D สรุปได้ว่า ด้าน A B AB A B 70 70 70
ตอบ