สวัสดีครับ สำหรับในตอนนี้พี่แม็คจะมาสรุปเนื้อหาของเวกเตอร์กันนะครับ ถ้าน้องๆ ยังไม่เข้าใจว่าเวกเตอร์มีหน้าตาเป็นยังไงและมีสาระสำคัญอย่างไรบ้าง ในบทความนี้พี่แม็คจะมาสรุปให้ฟังกันนะครับ
ปริมาณสเกลาร์ (scalar quantity) เป็นปริมาณที่มีเพียงแค่ขนาดอย่างเดียวปริมาณเวกเตอร์ (vector quantity) เป็นปริมาณที่บอกทั้งขนาดและทิศทาง
Ex. ตัวอย่างปริมาณสเกลาร์
ตัวอย่างปริมาณเวกเตอร์
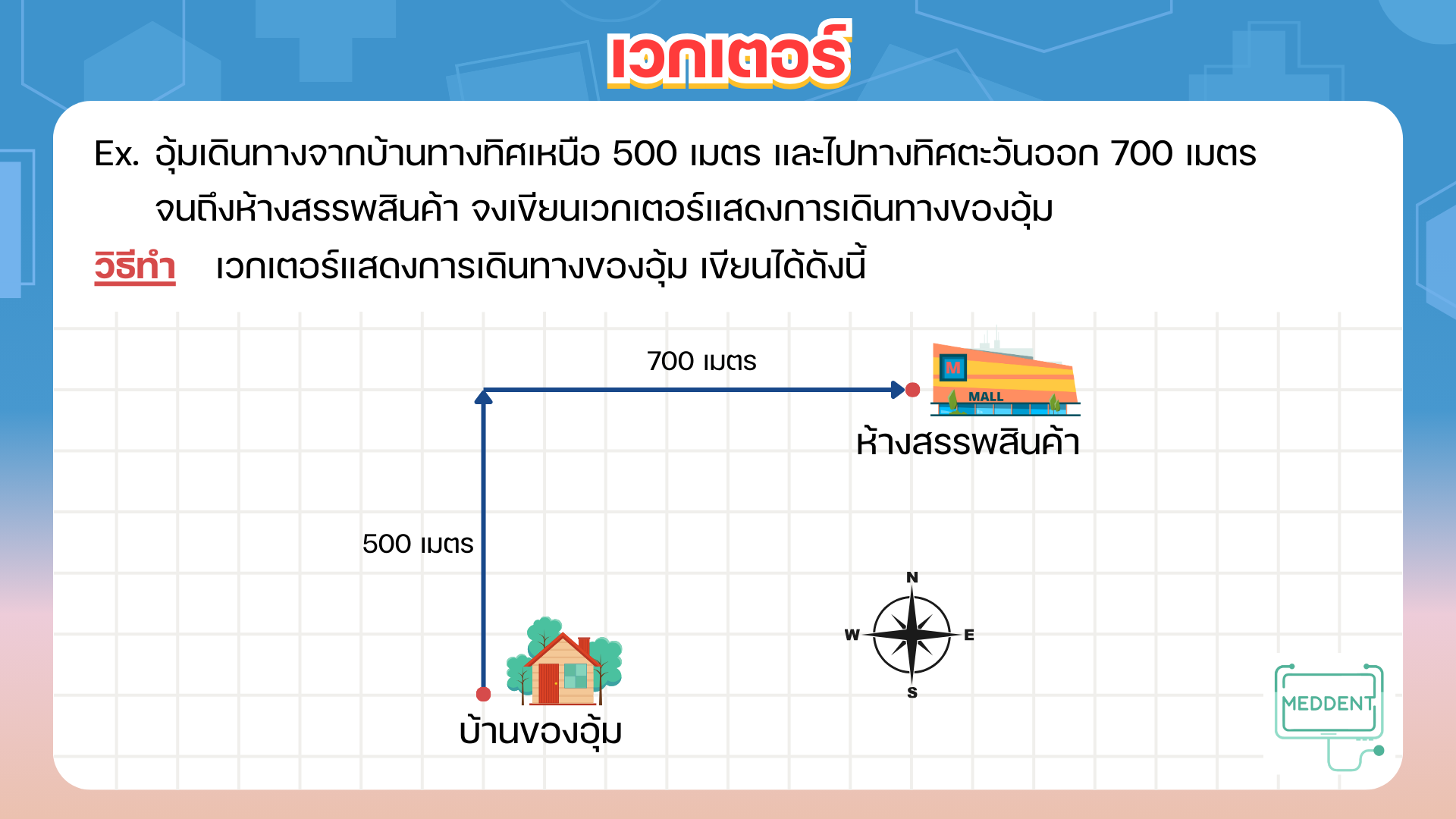
โดยปกติแล้ว ปริมาณสเกลาร์หรือเรียกสั้น ๆ ว่า สเกลาร์ จะแทนด้วยจำนวนจริง เวกเตอร์ จะแทนด้วยส่วนของเส้นตรงที่ระ บุ ทิศทาง
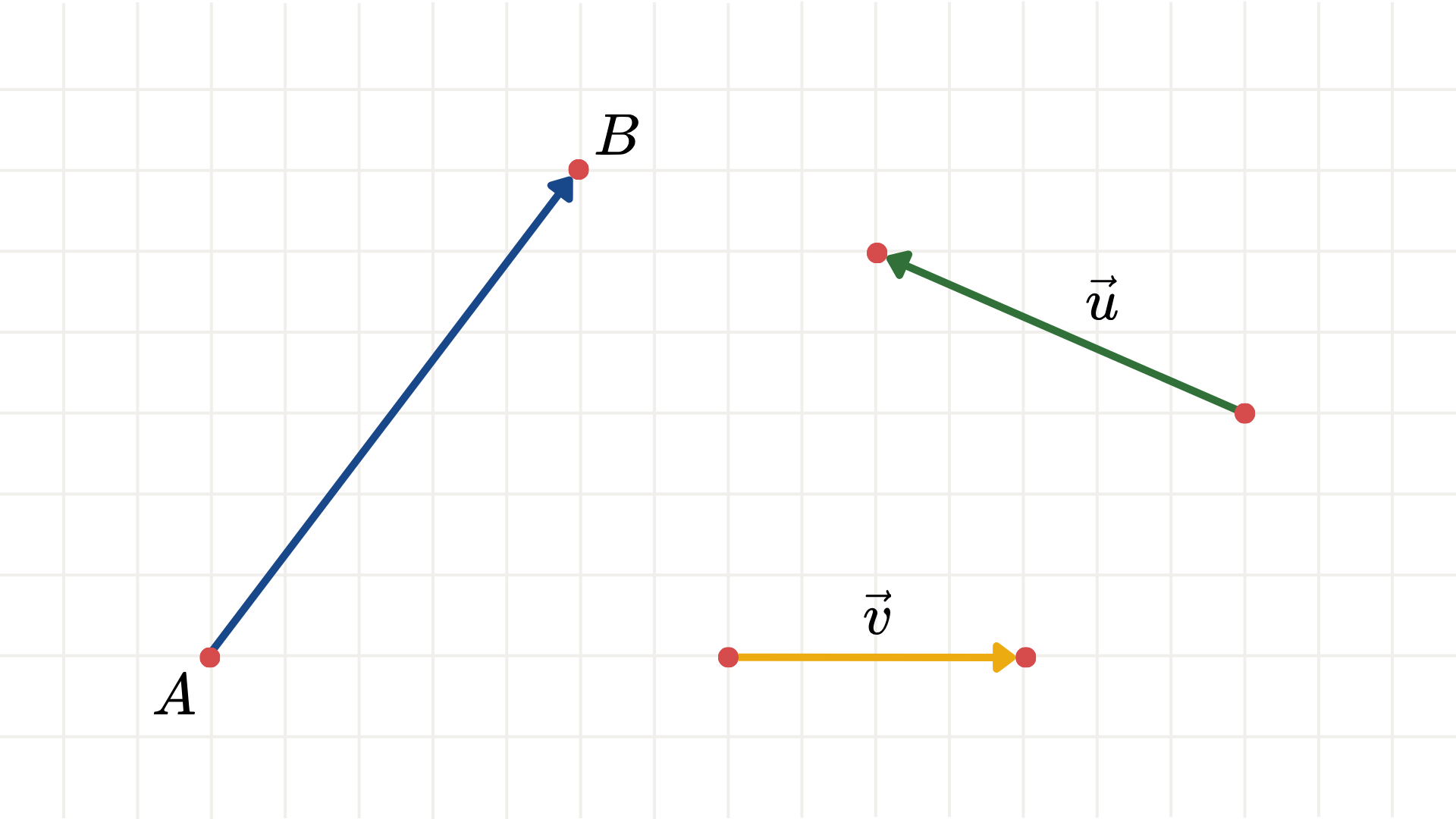
เวกเตอร์จากจุด A A A B B B A B → \overrightarrow{AB} A B เรียกจุด A A A จุดเริ่มต้น (initial point) และจุด B B B จุดสิ้นสุด (terminal point)ในบางครั้งอาจเขียนแทนเวกเตอร์ u ⃗ \vec{u} u v ⃗ \vec{v} v
ขนาด (magnitude) ของเวกเตอร์ u ⃗ \vec{u} u ∣ u ⃗ ∣ \left|\vec{u}\right| ∣ u ∣
เวกเตอร์ศูนย์ (zero vector) เขียนแทนด้วย 0 ⃗ \vec{0} 0 0 0 0
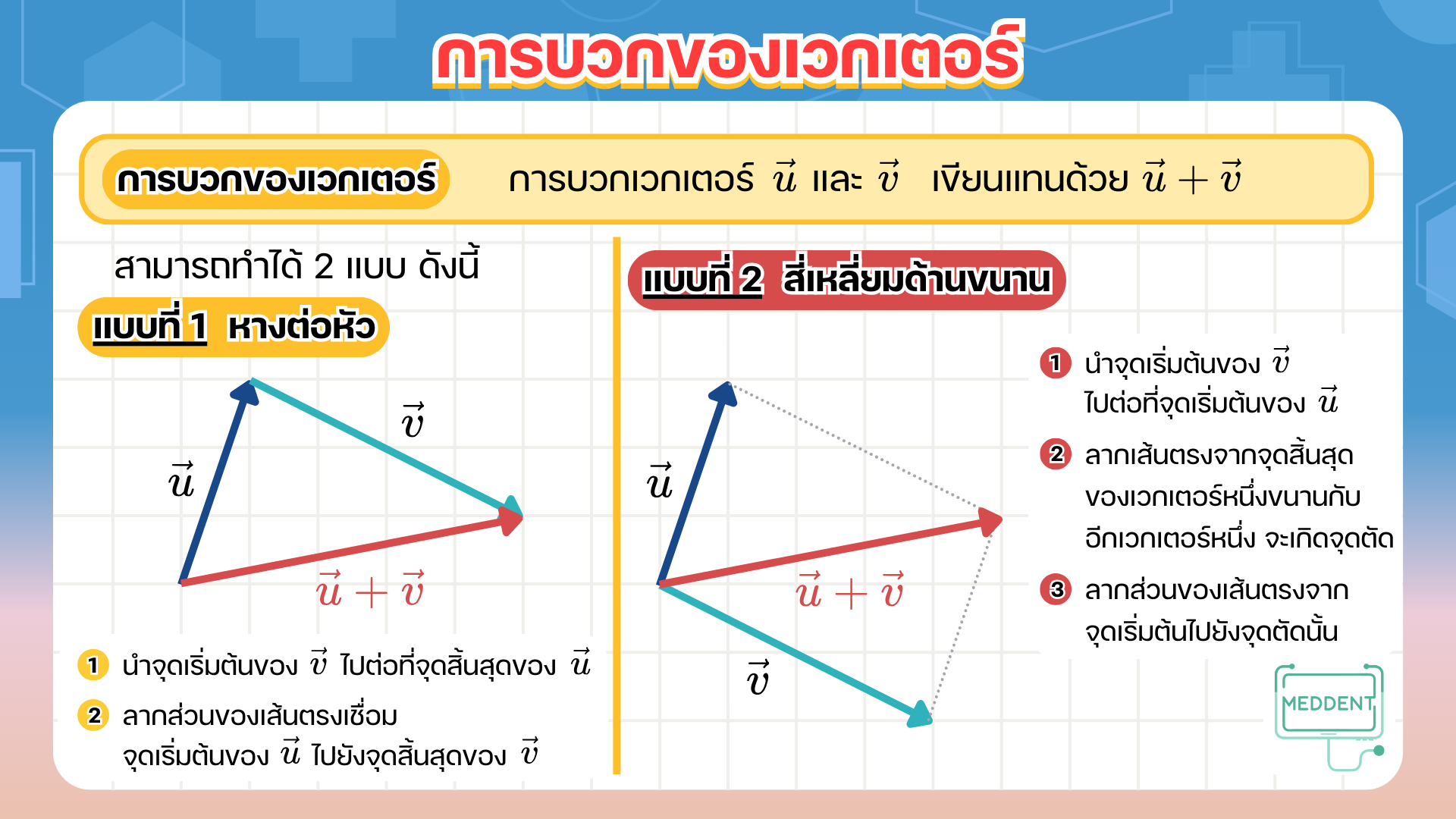
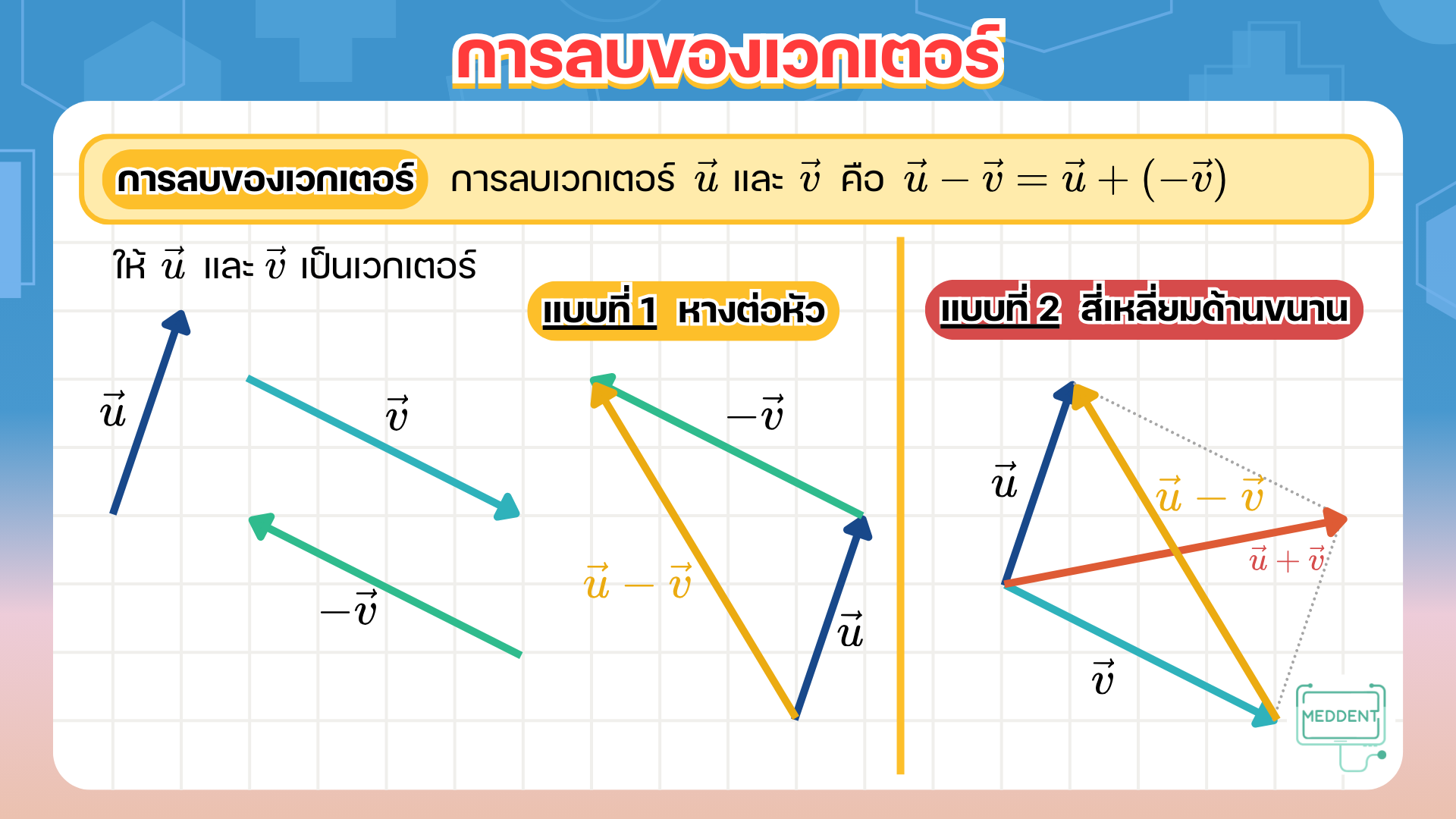
สมบัติการบวกของเวกเตอร์ ให้ u ⃗ , v ⃗ \vec{u}, \vec{v} u , v w ⃗ \vec{w} w
u ⃗ + v ⃗ = v ⃗ + u ⃗ \vec{u}+\vec{v} = \vec{v}+\vec{u} u + v = v + u ( u ⃗ + v ⃗ ) + w ⃗ = u ⃗ + ( v ⃗ + w ⃗ ) (\vec{u}+\vec{v})+\vec{w} = \vec{u}+(\vec{v}+\vec{w}) ( u + v ) + w = u + ( v + w ) u ⃗ + 0 ⃗ = 0 ⃗ + u ⃗ = u ⃗ \vec{u}+\vec{0} = \vec{0}+\vec{u} = \vec{u} u + 0 = 0 + u = u u ⃗ + ( − u ⃗ ) = ( − u ⃗ ) + u ⃗ = 0 ⃗ \vec{u}+(-\vec{u}) = (-\vec{u})+\vec{u} = \vec{0} u + ( − u ) = ( − u ) + u = 0 สมบัติการคูณเวกเตอร์ด้วยสเกลาร์ ให้ u ⃗ , v ⃗ \vec{u}, \vec{v} u , v a , b a,b a , b
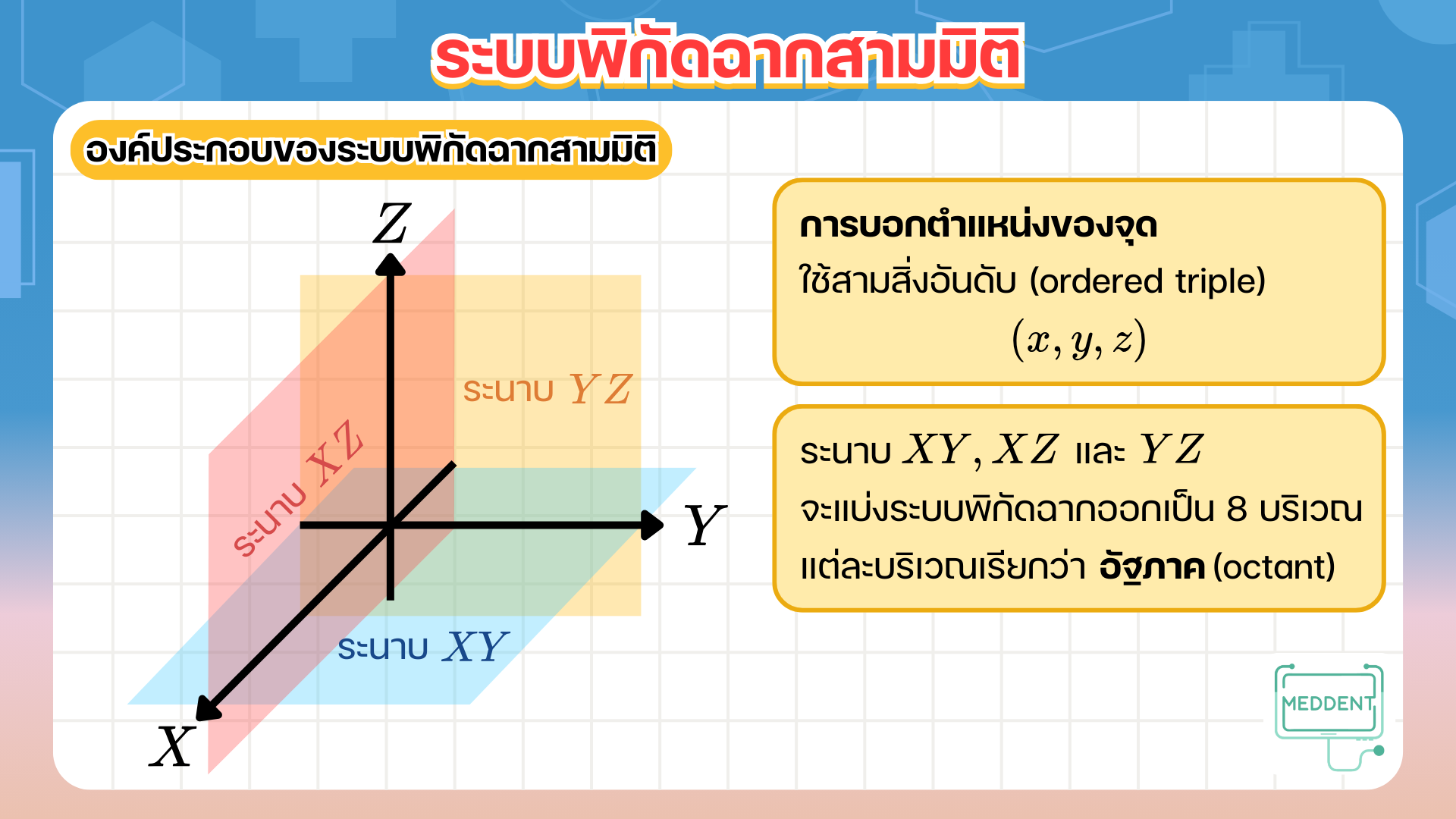
1 u ⃗ = u ⃗ 1\vec{u} = \vec{u} 1 u = u a ( u ⃗ + v ⃗ ) = a u ⃗ + a v ⃗ a(\vec{u}+\vec{v}) = a\vec{u}+a\vec{v} a ( u + v ) = a u + a v ( a + b ) u ⃗ = a u ⃗ + b u ⃗ (a+b)\vec{u} = a\vec{u}+b\vec{u} ( a + b ) u = a u + b u ( a b ) u ⃗ = a ( b u ⃗ ) = b ( a u ⃗ ) (ab)\vec{u} = a(b\vec{u}) = b(a\vec{u}) ( ab ) u = a ( b u ) = b ( a u ) การหาระยะห่างระหว่างจุดสองจุดบนระบบพิกัดฉากสามมิติ ให้ P ( x 1 , y 1 , z 1 ) P(x_1,y_1,z_1) P ( x 1 , y 1 , z 1 ) Q ( x 2 , y 2 , z 2 ) Q(x_2,y_2,z_2) Q ( x 2 , y 2 , z 2 ) ระยะห่างระหว่างจุด P P P Q Q Q ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 และเขียนแทนระยะห่างระหว่างจุด P P P Q Q Q ∣ P Q ∣ \left|PQ\right| ∣ PQ ∣
Ex. จงหาระยะห่างระหว่างจุด P ( 0 , 4 , 1 ) P(0,4,1) P ( 0 , 4 , 1 ) Q ( 3 , 1 , 4 ) Q(3,1,4) Q ( 3 , 1 , 4 ) วิธีทำ หาระยะห่างระหว่างจุด P P P Q Q Q
∣ P Q ∣ = ( 0 − 3 ) 2 + ( 4 − 1 ) 2 + ( 1 − 4 ) 2 = ( − 3 ) 2 + ( 3 ) 2 + ( − 3 ) 2 = 27 \begin{align*} \left|PQ\right| &= \sqrt{(0-3)^2+(4-1)^2+(1-4)^2} \\ &= \sqrt{(-3)^2+(3)^2+(-3)^2} \\ &= \sqrt{27} \end{align*} ∣ PQ ∣ = ( 0 − 3 ) 2 + ( 4 − 1 ) 2 + ( 1 − 4 ) 2 = ( − 3 ) 2 + ( 3 ) 2 + ( − 3 ) 2 = 27
ดังนั้น ระยะห่างระหว่างจุด P ( 0 , 4 , 1 ) P(0,4,1) P ( 0 , 4 , 1 ) Q ( 3 , 1 , 4 ) Q(3,1,4) Q ( 3 , 1 , 4 ) 27 \sqrt{27} 27
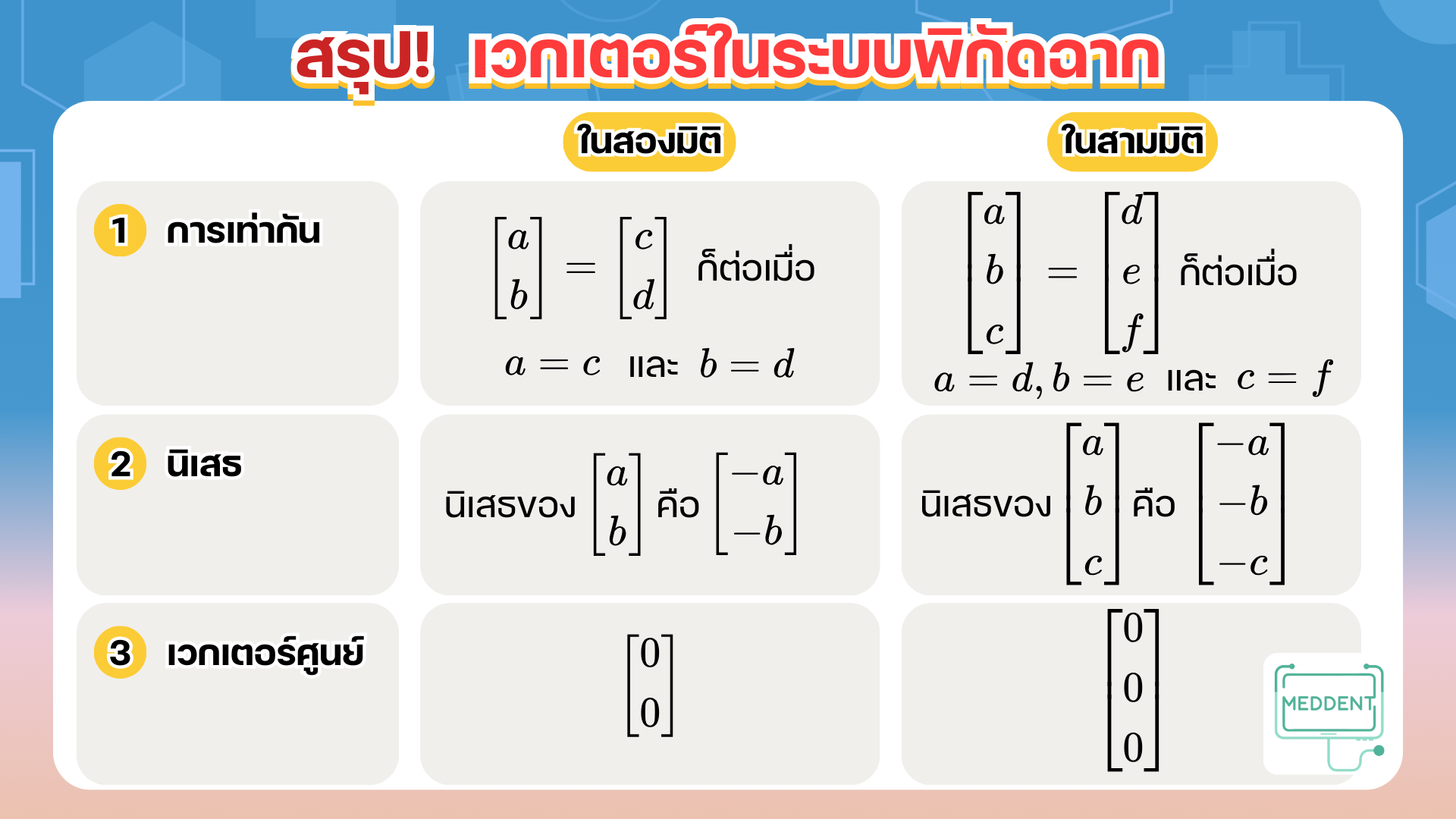
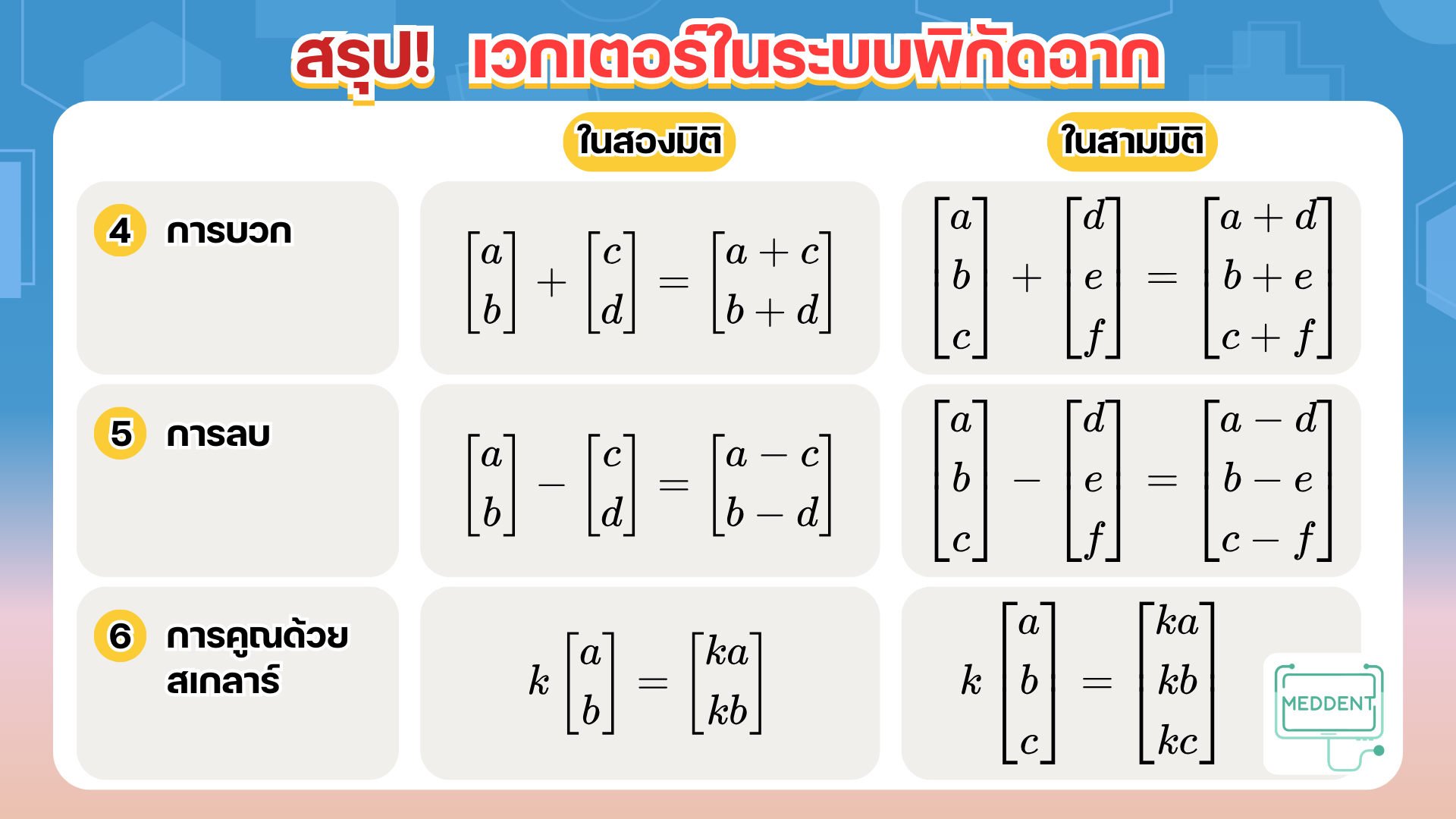
ในหัวข้อนี้พี่แม็คจะให้น้อง ๆ ลองหาเวกเตอร์ในระบบพิกัดฉากกัน แต่ก่อนอื่นพี่แม็คจะขอแนะนำเวกเตอร์ในระบบพิกัดฉากก่อน ดังนี้เลยค้าบบ
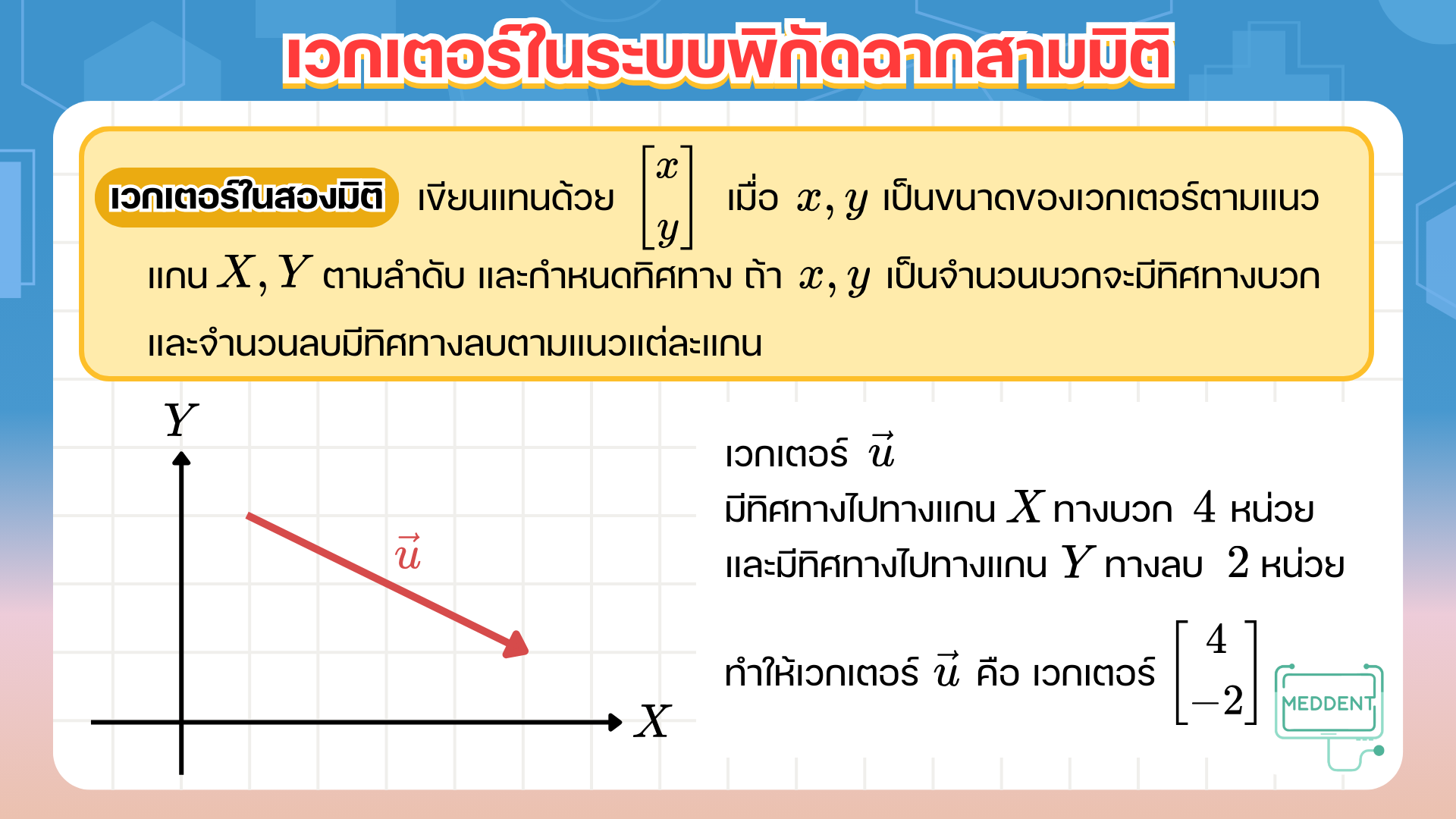
สำหรับเวกเตอร์ในสามมิติก็สามารถเขียนได้ในทำนองเดียวกัน นั่นคือ เขียนได้เป็นเวกเตอร์ [ x y z ] \begin{bmatrix} x \\ y \\ z \end{bmatrix} x y z โดยที่ x , y , z x,y,z x , y , z X , Y , Z X,Y,Z X , Y , Z ถ้า x , y , z x,y,z x , y , z แต่ถ้า x , y , z x,y,z x , y , z
ถ้าเกิดว่าน้อง ๆ รู้เพียงจุดเริ่มต้นและจุดสิ้นสุดจะสามารถเวกเตอร์ได้ โดยการนำจุดสิ้นสุดตั้งแล้วลบด้วยจุดเริ่มต้นTIPS การหาเวกเตอร์ในระบบพิกัดฉาก จะได้ว่า เวกเตอร์ = = = − - −
สำหรับเวกเตอร์ในระบบพิกัดฉากสองมิติ Ex. กำหนดให้ u ⃗ \vec{u} u P ( 2 , 5 ) P(2,5) P ( 2 , 5 ) Q ( 3 , − 4 ) Q(3,-4) Q ( 3 , − 4 ) จงหาเวกเตอร์ u ⃗ \vec{u} u วิธีทำ หาเวกเตอร์ u ⃗ \vec{u} u − - −
u ⃗ = [ 3 − 2 − 4 − 5 ] = [ 1 − 9 ] \begin{align*} \vec{u} = \begin{bmatrix} 3 - 2 \\ -4 - 5 \end{bmatrix} =\begin{bmatrix} 1 \\ -9 \end{bmatrix} \end{align*} u = [ 3 − 2 − 4 − 5 ] = [ 1 − 9 ]
ดังนั้น u ⃗ = [ 1 − 9 ] \vec{u} = \begin{bmatrix} 1 \\ -9 \end{bmatrix} u = [ 1 − 9 ]
Ex. กำหนดให้ A ( − 2 , 1 ) A(-2,1) A ( − 2 , 1 ) B ( 2 , 3 ) B(2,3) B ( 2 , 3 ) A B → \overrightarrow{AB} A B B A → \overrightarrow{BA} B A วิธีทำ เนื่องจากเวกเตอร์ A B → \overrightarrow{AB} A B A A A B B B
A B → = [ 2 − ( − 2 ) 3 − ( 1 ) ] = [ 4 2 ] \begin{align*} \overrightarrow{AB} &= \begin{bmatrix} 2 - (-2) \\ 3 - (1) \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \end{bmatrix} \end{align*} A B = [ 2 − ( − 2 ) 3 − ( 1 ) ] = [ 4 2 ]
และจากเวกเตอร์ B A → \overrightarrow{BA} B A B B B A A A
B A → = [ ( − 2 ) − 2 1 − 3 ] = [ − 4 − 2 ] \begin{align*} \overrightarrow{BA} &= \begin{bmatrix} (-2) - 2 \\ 1 - 3 \end{bmatrix} = \begin{bmatrix} -4 \\ -2 \end{bmatrix} \end{align*} B A = [ ( − 2 ) − 2 1 − 3 ] = [ − 4 − 2 ]
ตรงนี้น้อง ๆ อาจจะต้องระวังจุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์ให้ดี ๆ นะครับเพราะจากตัวอย่างที่ผ่านมาทำให้เห็นว่า เวกเตอร์ A B → \overrightarrow{AB} A B B A → \overrightarrow{BA} B A
สำหรับเวกเตอร์ในระบบพิกัดฉากสามมิติ Ex. กำหนดให้ u ⃗ \vec{u} u P ( 0 , 4 , 1 ) P(0,4,1) P ( 0 , 4 , 1 ) Q ( 3 , 1 , 4 ) Q(3,1,4) Q ( 3 , 1 , 4 ) จงหาเวกเตอร์ u ⃗ \vec{u} u วิธีทำ หาเวกเตอร์ u ⃗ \vec{u} u − - −
u ⃗ = [ 3 − 0 1 − 4 4 − 1 ] = [ 3 − 3 3 ] \begin{align*} \vec{u} = \begin{bmatrix} 3 - 0 \\ 1 - 4 \\ 4 - 1 \end{bmatrix} =\begin{bmatrix} 3 \\ -3 \\ 3 \end{bmatrix} \end{align*} u = 3 − 0 1 − 4 4 − 1 = 3 − 3 3
ดังนั้น u ⃗ = [ 3 − 3 3 ] \vec{u} = \begin{bmatrix} 3 \\ -3 \\ 3 \end{bmatrix} u = 3 − 3 3
Ex. ให้ v ⃗ = [ 5 − 1 − 2 ] \vec{v} = \begin{bmatrix} 5 \\ -1 \\ -2 \end{bmatrix} v = 5 − 1 − 2 P ( − 3 , − 2 , 7 ) P(-3,-2,7) P ( − 3 , − 2 , 7 ) จงหาจุดสิ้นสุดของเวกเตอร์ v ⃗ \vec{v} v วิธีทำ ให้ Q ( x , y , z ) Q(x,y,z) Q ( x , y , z ) v ⃗ \vec{v} v
v ⃗ = [ x − ( − 3 ) y − ( − 2 ) z − 7 ] = [ x + 3 y + 2 z − 7 ] \begin{align*} \vec{v} &= \begin{bmatrix} x - (-3) \\ y - (-2) \\ z - 7 \end{bmatrix} = \begin{bmatrix} x + 3 \\ y + 2 \\ z - 7 \end{bmatrix} \end{align*} v = x − ( − 3 ) y − ( − 2 ) z − 7 = x + 3 y + 2 z − 7
เนื่องจาก v ⃗ = [ 5 − 1 − 2 ] \vec{v} = \begin{bmatrix} 5 \\ -1 \\ -2 \end{bmatrix} v = 5 − 1 − 2 [ x + 3 y + 2 z − 7 ] = [ 5 − 1 − 2 ] \begin{bmatrix} x + 3 \\ y + 2 \\ z - 7 \end{bmatrix} = \begin{bmatrix} 5 \\ -1 \\ -2 \end{bmatrix} x + 3 y + 2 z − 7 = 5 − 1 − 2 ดังนั้น x + 3 = 5 , y + 2 = − 1 x+3 = 5,\ y+2 = -1 x + 3 = 5 , y + 2 = − 1 z − 7 = − 2 z-7 = -2 z − 7 = − 2 เพราะฉะนั้น จุดสิ้นสุดของเวกเตอร์ v ⃗ \vec{v} v Q Q Q ( x , y , z ) = ( 2 , − 3 , 5 ) (x,y,z) = (2, -3, 5) ( x , y , z ) = ( 2 , − 3 , 5 )
ขนาดของเวกเตอร์ ให้ v ⃗ \vec{v} v v ⃗ \vec{v} v ∣ v ⃗ ∣ \left|\vec{v}\right| ∣ v ∣
สำหรับสองมิติ: ถ้า v ⃗ = [ a b ] \vec{v} = \begin{bmatrix} a \\ b \end{bmatrix} v = [ a b ] v ⃗ \vec{v} v ∣ v ⃗ ∣ = a 2 + b 2 \left|\vec{v}\right| =\sqrt{a^2+b^2} ∣ v ∣ = a 2 + b 2 สำหรับสามมิติ: ถ้า v ⃗ = [ a b c ] \vec{v} = \begin{bmatrix} a \\ b \\ c \end{bmatrix} v = a b c v ⃗ \vec{v} v ∣ v ⃗ ∣ = a 2 + b 2 + c 2 \left|\vec{v}\right| =\sqrt{a^2+b^2+c^2} ∣ v ∣ = a 2 + b 2 + c 2
Ex. กำหนดให้ u ⃗ = [ 3 − 4 ] \vec{u} = \begin{bmatrix} 3 \\ -4 \end{bmatrix} u = [ 3 − 4 ] u ⃗ \vec{u} u วิธีทำ ขนาดของเวกเตอร์ u ⃗ \vec{u} u ∣ u ⃗ ∣ = 3 2 + ( − 4 ) 2 = 9 + 16 = 25 = 5 \left|\vec{u}\right| =\sqrt{3^2+(-4)^2} = \sqrt{9+16} = \sqrt{25} = 5 ∣ u ∣ = 3 2 + ( − 4 ) 2 = 9 + 16 = 25 = 5
Ex. กำหนดให้ v ⃗ = [ 3 − 1 2 ] \vec{v} = \begin{bmatrix} 3 \\ -1 \\ 2 \end{bmatrix} v = 3 − 1 2 v ⃗ \vec{v} v วิธีทำ ขนาดของ v ⃗ \vec{v} v ∣ v ⃗ ∣ = 3 2 + ( − 1 ) 2 + 2 2 = 9 + 1 + 4 = 15 \left|\vec{v}\right| =\sqrt{3^2+(-1)^2+2^2} = \sqrt{9+1+4} = \sqrt{15} ∣ v ∣ = 3 2 + ( − 1 ) 2 + 2 2 = 9 + 1 + 4 = 15
เวกเตอร์หนึ่งหน่วย เวกเตอร์หนึ่งหน่วย คือ เวกเตอร์ที่มีขนาด 1 หน่วย
Ex. กำหนดให้ u ⃗ = [ 3 − 4 ] \vec{u} = \begin{bmatrix} 3 \\ -4 \end{bmatrix} u = [ 3 − 4 ] จงหาเวกเตอร์หนึ่งหน่วยที่มีทิศทางเดียวกับเวกเตอร์ u ⃗ \vec{u} u u ⃗ \vec{u} u วิธีทำ เนื่องจากขนาดของเวกเตอร์ u ⃗ \vec{u} u 5 5 5 เวกเตอร์หนึ่งหน่วยที่มีทิศทางเดียวกับเวกเตอร์ u ⃗ \vec{u} u u ⃗ ∣ u ⃗ ∣ = 1 5 [ 3 − 4 ] = [ 3 5 − 4 5 ] \displaystyle\frac{\vec{u}}{\left|\vec{u}\right|} = \displaystyle\frac{1}{5}\begin{bmatrix} 3 \\ -4 \end{bmatrix} = \begin{bmatrix} \displaystyle\frac{3}{5} \\ -\displaystyle\frac{4}{5} \end{bmatrix} ∣ u ∣ u = 5 1 [ 3 − 4 ] = 5 3 − 5 4 และเวกเตอร์หนึ่งหน่วยที่มีทิศทางตรงข้ามกับเวกเตอร์ u ⃗ \vec{u} u − u ⃗ ∣ u ⃗ ∣ = − 1 5 [ 3 − 4 ] = [ − 3 5 4 5 ] -\displaystyle\frac{\vec{u}}{\left|\vec{u}\right|} = -\displaystyle\frac{1}{5}\begin{bmatrix} 3 \\ -4 \end{bmatrix} = \begin{bmatrix} -\displaystyle\frac{3}{5} \\ \displaystyle\frac{4}{5} \end{bmatrix} − ∣ u ∣ u = − 5 1 [ 3 − 4 ] = − 5 3 5 4
ให้ u ⃗ \vec{u} u v ⃗ \vec{v} v ผลคูณเชิงสเกลาร์ (dot product) ของ u ⃗ \vec{u} u v ⃗ \vec{v} v u ⃗ ⋅ v ⃗ \vec{u}\cdot\vec{v} u ⋅ v
สำหรับสองมิติ: ถ้า u ⃗ = [ u 1 u 2 ] \vec{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} u = [ u 1 u 2 ] v ⃗ = [ v 1 v 2 ] \vec{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} v = [ v 1 v 2 ] u ⃗ ⋅ v ⃗ = u 1 v 1 + u 2 v 2 \vec{u}\cdot\vec{v} = u_1v_1 + u_2v_2 u ⋅ v = u 1 v 1 + u 2 v 2 สำหรับสามมิติ: ถ้า u ⃗ = [ u 1 u 2 u 3 ] \vec{u} = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} u = u 1 u 2 u 3 v ⃗ = [ v 1 v 2 v 3 ] \vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} v = v 1 v 2 v 3 u ⃗ ⋅ v ⃗ = u 1 v 1 + u 2 v 2 + u 3 v 3 \vec{u}\cdot\vec{v} = u_1v_1 + u_2v_2 + u_3v3 u ⋅ v = u 1 v 1 + u 2 v 2 + u 3 v 3
Ex. กำหนดให้ u ⃗ = [ 3 − 4 ] \vec{u} = \begin{bmatrix} 3 \\ -4 \end{bmatrix} u = [ 3 − 4 ] v ⃗ = [ − 2 1 ] \vec{v} = \begin{bmatrix} -2 \\ 1 \end{bmatrix} v = [ − 2 1 ] u ⃗ ⋅ v ⃗ \vec{u}\cdot\vec{v} u ⋅ v วิธีทำ u ⃗ ⋅ v ⃗ = 3 ⋅ ( − 2 ) + ( − 4 ) ⋅ 1 = ( − 6 ) + ( − 4 ) = − 10 \vec{u}\cdot\vec{v} = 3\cdot(-2) + (-4)\cdot 1 = (-6)+(-4) = -10 u ⋅ v = 3 ⋅ ( − 2 ) + ( − 4 ) ⋅ 1 = ( − 6 ) + ( − 4 ) = − 10
Ex. กำหนดให้ u ⃗ = [ 12 − 5 1 ] \vec{u} = \begin{bmatrix} 12 \\ -5 \\ 1 \end{bmatrix} u = 12 − 5 1 v ⃗ = [ 1 2 − 3 ] \vec{v} = \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} v = 1 2 − 3 u ⃗ ⋅ v ⃗ \vec{u}\cdot\vec{v} u ⋅ v วิธีทำ u ⃗ ⋅ v ⃗ = 12 ⋅ 1 + ( − 5 ) ⋅ 2 + 1 ⋅ ( − 3 ) = 12 + ( − 10 ) + ( − 3 ) = − 1 \vec{u}\cdot\vec{v} = 12\cdot 1 + (-5)\cdot 2 + 1\cdot (-3) = 12+(-10)+(-3) = -1 u ⋅ v = 12 ⋅ 1 + ( − 5 ) ⋅ 2 + 1 ⋅ ( − 3 ) = 12 + ( − 10 ) + ( − 3 ) = − 1
ให้ u ⃗ = [ u 1 u 2 u 3 ] \vec{u} = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} u = u 1 u 2 u 3 v ⃗ = [ v 1 v 2 v 3 ] \vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} v = v 1 v 2 v 3 ผลคูณเชิงเวกเตอร์ (cross product) ของ u ⃗ \vec{u} u v ⃗ \vec{v} v u ⃗ × v ⃗ \vec{u}\times\vec{v} u × v [ u 2 v 3 − u 3 v 2 u 1 v 3 − u 3 v 1 u 1 v 2 − u 2 v 1 ] \begin{bmatrix} u_2v_3-u_3v_2 \\ u_1v_3-u_3v_1 \\ u_1v_2-u_2v_1 \end{bmatrix} u 2 v 3 − u 3 v 2 u 1 v 3 − u 3 v 1 u 1 v 2 − u 2 v 1
หมายเหตุ
u ⃗ × v ⃗ = ∣ i ⃗ j ⃗ k ⃗ u 1 u 2 u 3 v 1 v 2 v 3 ∣ i ⃗ j ⃗ u 1 u 2 v 1 v 2 = ( u 2 v 3 ) i ⃗ + ( u 1 v 3 ) j ⃗ + ( u 1 v 2 ) k ⃗ − ( u 2 v 1 ) k ⃗ − ( u 3 v 2 ) i ⃗ − ( u 3 v 1 ) j ⃗ = ( u 2 v 3 − u 3 v 2 ) i ⃗ + ( u 1 v 3 − u 3 v 1 ) j ⃗ + ( u 1 v 2 − u 2 v 1 ) k ⃗ \begin{align*}\vec{u}\times\vec{v} &= \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} {\color{gray}\begin{matrix} \vec{i} & \vec{j} \\ u_1 & u_2 \\ v_1 & v_2 \end{matrix}} \\ &= (u_2v_3)\vec{i} + (u_1v_3)\vec{j} + (u_1v_2)\vec{k} - (u_2v_1)\vec{k} - (u_3v_2)\vec{i} - (u_3v_1)\vec{j} \\ &= (u_2v_3-u_3v_2)\vec{i} + (u_1v_3-u_3v_1)\vec{j} + (u_1v_2-u_2v_1)\vec{k} \end{align*} u × v = i u 1 v 1 j u 2 v 2 k u 3 v 3 i u 1 v 1 j u 2 v 2 = ( u 2 v 3 ) i + ( u 1 v 3 ) j + ( u 1 v 2 ) k − ( u 2 v 1 ) k − ( u 3 v 2 ) i − ( u 3 v 1 ) j = ( u 2 v 3 − u 3 v 2 ) i + ( u 1 v 3 − u 3 v 1 ) j + ( u 1 v 2 − u 2 v 1 ) k
เมื่อ i ⃗ , j ⃗ , k ⃗ \vec{i}, \vec{j}, \vec{k} i , j , k X , Y X,Y X , Y Z Z Z
Ex. กำหนดให้ u ⃗ = [ 12 − 5 1 ] \vec{u} = \begin{bmatrix} 12 \\ -5 \\ 1 \end{bmatrix} u = 12 − 5 1 v ⃗ = [ 1 2 − 3 ] \vec{v} = \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} v = 1 2 − 3 u ⃗ × v ⃗ \vec{u}\times\vec{v} u × v วิธีทำ
u ⃗ × v ⃗ = ∣ i ⃗ j ⃗ k ⃗ 12 − 5 1 1 2 − 3 ∣ i ⃗ j ⃗ 12 − 5 1 2 = 15 i ⃗ + 1 j ⃗ + 24 k ⃗ − ( − 5 ) k ⃗ − 2 i ⃗ − ( − 36 ) j ⃗ = 13 i ⃗ + 37 j ⃗ + 29 k ⃗ \begin{align*}\vec{u}\times\vec{v} &= \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 12 & -5 & 1 \\ 1 & 2 & -3 \end{vmatrix} {\color{gray}\begin{matrix} \vec{i} & \vec{j} \\ 12 & -5 \\ 1 & 2 \end{matrix}} \\ &= 15\vec{i} + 1\vec{j} + 24\vec{k} - (-5)\vec{k} - 2\vec{i} - (-36)\vec{j} \\ &= 13\vec{i} + 37\vec{j} + 29\vec{k} \end{align*} u × v = i 12 1 j − 5 2 k 1 − 3 i 12 1 j − 5 2 = 15 i + 1 j + 24 k − ( − 5 ) k − 2 i − ( − 36 ) j = 13 i + 37 j + 29 k
ดังนั้น u ⃗ × v ⃗ = [ 13 37 29 ] \vec{u}\times\vec{v} = \begin{bmatrix} 13 \\ 37 \\ 29 \end{bmatrix} u × v = 13 37 29
การหาผลคูณเชิงเวกเตอร์สามารถประยุกต์ในเรื่องต่าง ๆ ดังนี้1. พื้นที่ของรูปสี่เหลี่ยมด้านขนาน = ∣ u ⃗ × v ⃗ ∣ = \left|\vec{u} \times \vec{v}\right| = ∣ u × v ∣ 2. พื้นที่ของรูปสามเหลี่ยม = 1 2 ∣ u ⃗ × v ⃗ ∣ = \displaystyle\frac{1}{2}\left|\vec{u} \times \vec{v}\right| = 2 1 ∣ u × v ∣ 3. ปริมาตรของรูปทรงสี่เหลี่ยมด้านขนาน = ∣ u ⃗ ⋅ ( v ⃗ × w ⃗ ) ∣ = \left|\vec{u} \cdot (\vec{v}\times \vec{w})\right| = ∣ u ⋅ ( v × w ) ∣ เมื่อ u ⃗ , v ⃗ , w ⃗ \vec{u}, \vec{v}, \vec{w} u , v , w
กำหนดรูปสามเหลี่ยม A B C ABC A BC A ( − 2 , − 4 , − 4 ) , B ( 0 , − 2 , 0 ) A(-2,-4,-4),\ B(0,-2,0) A ( − 2 , − 4 , − 4 ) , B ( 0 , − 2 , 0 ) C ( 0 , 0 , 2 ) C(0,0,2) C ( 0 , 0 , 2 ) A B C ABC A BC
1 1 1 3 \sqrt{3} 3 2 2 2 2 3 2\sqrt{3} 2 3 4 3 4\sqrt{3} 4 3 วิธีทำ จากสูตรพื้นที่ของรูปสามเหลี่ยม = 1 2 ∣ A B → × A C → ∣ = \displaystyle\frac{1}{2}\left|\overrightarrow{AB} \times \overrightarrow{AC}\right| = 2 1 A B × A C A ( − 2 , − 2 , − 4 ) , B ( 0 , − 2 , 0 ) A(-2,-2,-4),\ B(0,-2,0) A ( − 2 , − 2 , − 4 ) , B ( 0 , − 2 , 0 ) C ( 0 , 0 , 2 ) C(0,0,2) C ( 0 , 0 , 2 ) A B → = [ 0 − ( − 2 ) − 2 − ( − 4 ) 0 − ( − 4 ) ] = [ 2 2 4 ] \overrightarrow{AB} = \begin{bmatrix} 0-(-2) \\ -2-(-4) \\ 0-(-4) \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 4 \end{bmatrix} A B = 0 − ( − 2 ) − 2 − ( − 4 ) 0 − ( − 4 ) = 2 2 4 A C → = [ 0 − ( − 2 ) 0 − ( − 4 ) 2 − ( − 4 ) ] = [ 2 4 6 ] \overrightarrow{AC} = \begin{bmatrix} 0-(-2) \\ 0-(-4) \\ 2-(-4) \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix} A C = 0 − ( − 2 ) 0 − ( − 4 ) 2 − ( − 4 ) = 2 4 6 นั่นคือ A B → = 2 i ⃗ + 2 j ⃗ + 4 k ⃗ \overrightarrow{AB} = 2\vec{i} + 2\vec{j} + 4\vec{k} A B = 2 i + 2 j + 4 k A C → = 2 i ⃗ + 4 j ⃗ + 6 k ⃗ \overrightarrow{AC} = 2\vec{i} + 4\vec{j} + 6\vec{k} A C = 2 i + 4 j + 6 k
จะได้ว่า
A B → × A C → = ∣ i ⃗ j ⃗ k ⃗ 2 2 4 2 4 6 ∣ i ⃗ j ⃗ 2 2 2 4 = 12 i ⃗ + 8 j ⃗ + 8 k ⃗ − 4 k ⃗ − 16 i ⃗ − 12 j ⃗ = − 4 i ⃗ − 4 j ⃗ + 4 k ⃗ \begin{align*}\overrightarrow{AB} \times \overrightarrow{AC} &= \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 2 & 2 & 4 \\ 2 & 4 & 6 \end{vmatrix} {\color{gray}\begin{matrix} \vec{i} & \vec{j} \\ 2 & 2 \\ 2 & 4 \end{matrix}} \\ &= 12\vec{i} + 8\vec{j} + 8\vec{k} - 4\vec{k} - 16\vec{i} - 12\vec{j} \\ &= -4\vec{i} -4\vec{j} + 4\vec{k} \end{align*} A B × A C = i 2 2 j 2 4 k 4 6 i 2 2 j 2 4 = 12 i + 8 j + 8 k − 4 k − 16 i − 12 j = − 4 i − 4 j + 4 k
ดังนั้น ∣ A B → × A C → ∣ = ( − 4 ) 2 + ( − 4 ) 2 + 4 2 = 16 + 16 + 16 = 3 ⋅ 16 = 4 3 \left|\overrightarrow{AB} \times \overrightarrow{AC}\right| = \sqrt{(-4)^2+(-4)^2+4^2} = \sqrt{16+16+16} = \sqrt{3\cdot 16} = 4\sqrt{3} A B × A C = ( − 4 ) 2 + ( − 4 ) 2 + 4 2 = 16 + 16 + 16 = 3 ⋅ 16 = 4 3
เพราะฉะนั้น พื้นที่ของรูปสามเหลี่ยม = 1 2 ∣ A B → × A C → ∣ = 1 2 ⋅ ( 4 3 ) = 2 3 = \displaystyle\frac{1}{2}\left|\overrightarrow{AB} \times \overrightarrow{AC}\right| = \displaystyle\frac{1}{2}\cdot(4\sqrt{3}) = 2\sqrt{3} = 2 1 A B × A C = 2 1 ⋅ ( 4 3 ) = 2 3
ตอบ ข้อ 4. 2 3 2\sqrt{3} 2 3