
รวมข้อง่าย คณิต 2 A-Level
มกราคม 24, 2026
ช่วงนี้เป็นโค้งสุดท้ายที่น้อง ๆ หลายคนกำลังอ่านหนังสือเพื่อเตรียมสอบเข้ามหาวิทยาลัยกัน ในบทความนี้ พี่แม็คจะพาให้น้อง ๆ มาลองดูกันกับข้อสอบเข้ามหาวิทยาลัยที่เคยออกสอบมาแล้ว แต่อยู่ในระดับความยากและมีเนื้อหาเดียวกันกับวิชาคณิตศาสตร์ประยุกต์ 2 A-Level กัน ถ้าน้อง ๆ พร้อมแล้ว มาเริ่มกันเล้ยย!
คำถาม
1. ครอบครัวหนึ่งมีสมาชิก คน มี คนที่ชอบดูสารคดี มี คนที่ชอบดูละคร และมี คนที่ไม่ชอบดูทั้งสารคดีและละคร จำนวนคนในครอบครัวนี้ที่ชอบดูสารคดี แต่ไม่ชอบดูละครเท่ากับเท่าใด
- คน
- คน
- คน
- คน
- คน
2. กำหนดให้ เป็นประพจน์ที่มีค่าความจริงเป็นจริงและเท็จ ตามลำดับ
ประพจน์ในข้อใดต่อไปนี้มีค่าความจริงเป็นจริง
3. กำหนดให้ เป็นฟังก์ชันเชิงเส้น ถ้า และ แล้ว เท่ากับเท่าใด
4. เท่ากับเท่าใด
5. ถ้า แล้วผลบวก พจน์แรกของลำดับนี้เท่ากับข้อใดต่อไปนี้
6. ข้อสอบแบบเลือกคำตอบชุดหนึ่งมี ข้อ แต่ละข้อมี ตัวเลือก และมีตัวเลือกที่ถูกเพียงตัวเลือกเดียว
ถ้านายสบโชคเดาคำตอบแต่ละข้ออย่างสุ่ม ข้อละ ตัวเลือก ความน่าจะเป็นที่นายสบโชคจะเดาคำตอบผิดหมดทุกข้อเท่ากับข้อใดต่อไปนี้
7. ข้อมูลชุดใดต่อไปนี้ที่ มัธยฐาน ฐานนิยม
8. จากผลการสอบวิชาคณิตศาสตร์ของนักเรียนระดับชั้น ม.4 ซึ่งประกอบด้วยห้อง ม.4/1 และ ม.4/2 ที่มีจำนวนนักเรียนห้องละ คนเท่ากัน ได้ผลสรุปของคะแนนสอบเป็นแผนภาพกล่องดังนี้
ถ้าในการสอบครั้งนี้ครูให้ระดับคะแนน แก่ผู้ที่สอบได้คะแนนน้อยกว่า คะแนน และให้ระดับคะแนน แก่ผู้ที่สอบได้คะแนนมากกว่า คะแนน
แล้วพิจารณาข้อความต่อไปนี้
ก. พิสัยของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
ข. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
ค. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
ง. ค่าเฉลี่ยเลขคณิตของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
จำนวนข้อความที่ถูกต้อง เท่ากับข้อใดต่อไปนี้
- (ไม่มีข้อความใดถูก)
- มากกว่า
เฉลย
1. ครอบครัวหนึ่งมีสมาชิก คน มี คนที่ชอบดูสารคดี มี คนที่ชอบดูละคร และมี คนที่ไม่ชอบดูทั้งสารคดีและละคร จำนวนคนในครอบครัวนี้ที่ชอบดูสารคดี แต่ไม่ชอบดูละครเท่ากับเท่าใด
- คน
- คน
- คน
- คน
- คน
(ข้อสอบ A-Level คณิตศาสตร์ประยุกต์ 2 รอบ มี.ค. 68)
วิธีทำ
ให้ เป็นเอกภพสัมพัทธ์ของสมาชิกในครอบครัวนี้ จะได้ว่า
เป็นเซตของคนที่ชอบดูสารคดี จะได้ว่า
และ เป็นเซตของคนที่ชอบดูละคร จะได้ว่า
เนื่องจากมี คนที่ไม่ชอบดูทั้งสารคดีและละคร จะได้ว่า จำนวนคนที่ชอบดูสารคดีหรือละคร
เท่ากับ คน นั่นคือ
จากสูตร
จะได้ว่า
นั่นคือ ซึ่งสามารถวาดเป็นแผนภาพได้ดังนี้
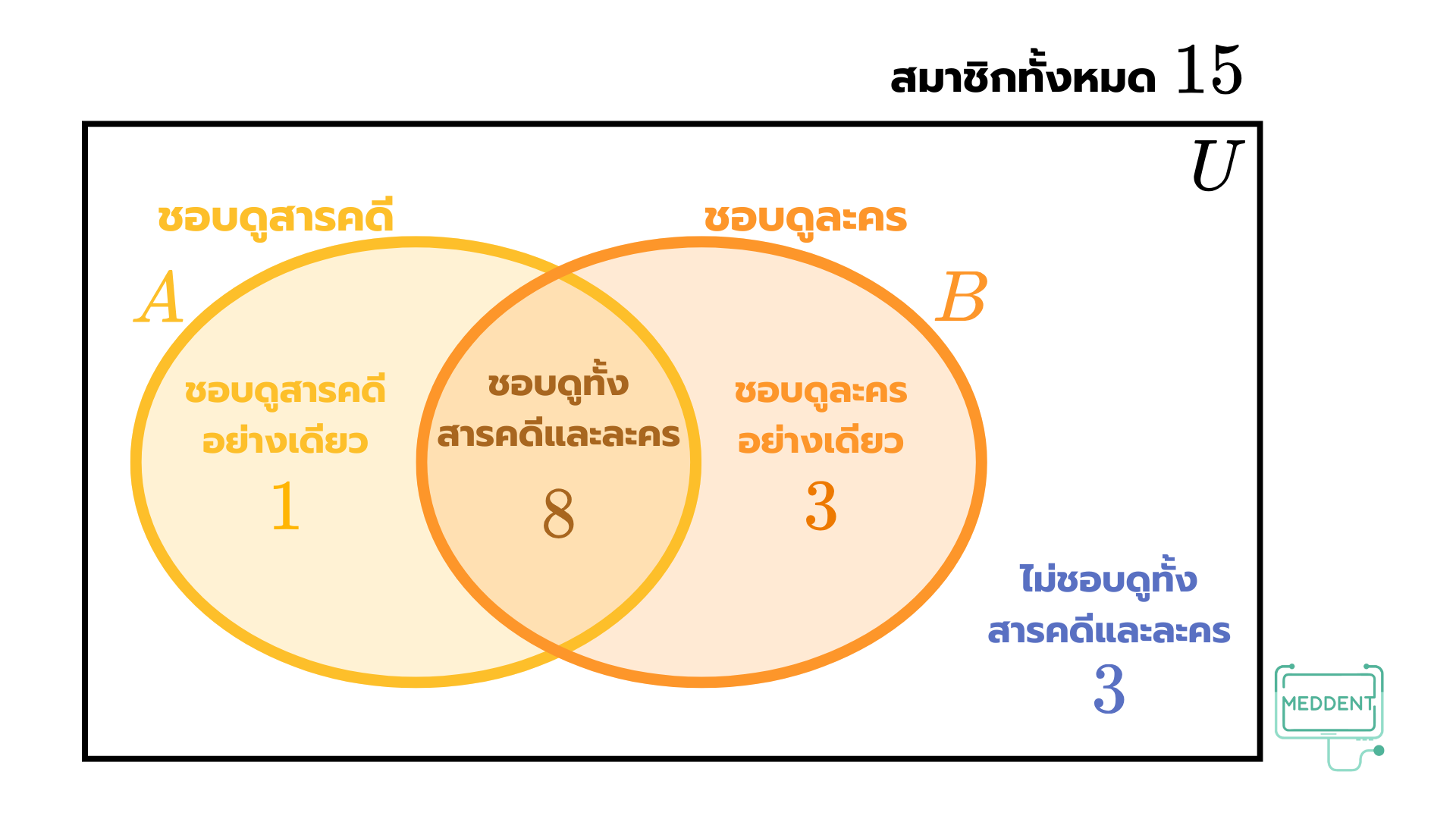
ดังนั้น คนในครอบครัวนี้ที่ชอบดูสารคดี แต่ไม่ชอบดูละครเท่ากับ คน
ตอบ ข้อ 1. คน
2. กำหนดให้ เป็นประพจน์ที่มีค่าความจริงเป็นจริงและเท็จ ตามลำดับ
ประพจน์ในข้อใดต่อไปนี้มีค่าความจริงเป็นจริง
(ข้อสอบ A-Level คณิตศาสตร์ประยุกต์ 2 รอบ มี.ค. 66)
วิธีทำ เนื่องจากประพจน์ " หรือ " จะเป็นเท็จในกรณีเดียวคือ ทั้ง และ ต่างเป็นเท็จทั้งคู่
ประพจน์ " และ " จะเป็นจริงในกรณีเดียวคือ ทั้ง และ ต่างเป็นจริงทั้งคู่
ประพจน์ "ถ้า แล้ว " จะเป็นเท็จในกรณีเดียวคือ ประพจน์ เป็นจริงและ เป็นเท็จ
ประพจน์ " ก็ต่อเมื่อ " จะเป็นจริง เมื่อ ทั้ง และ ต่างมีค่าความจริงเหมือนกันทั้งคู่
ซึ่งสามารถเขียนเป็นแผนภาพได้ดังนี้
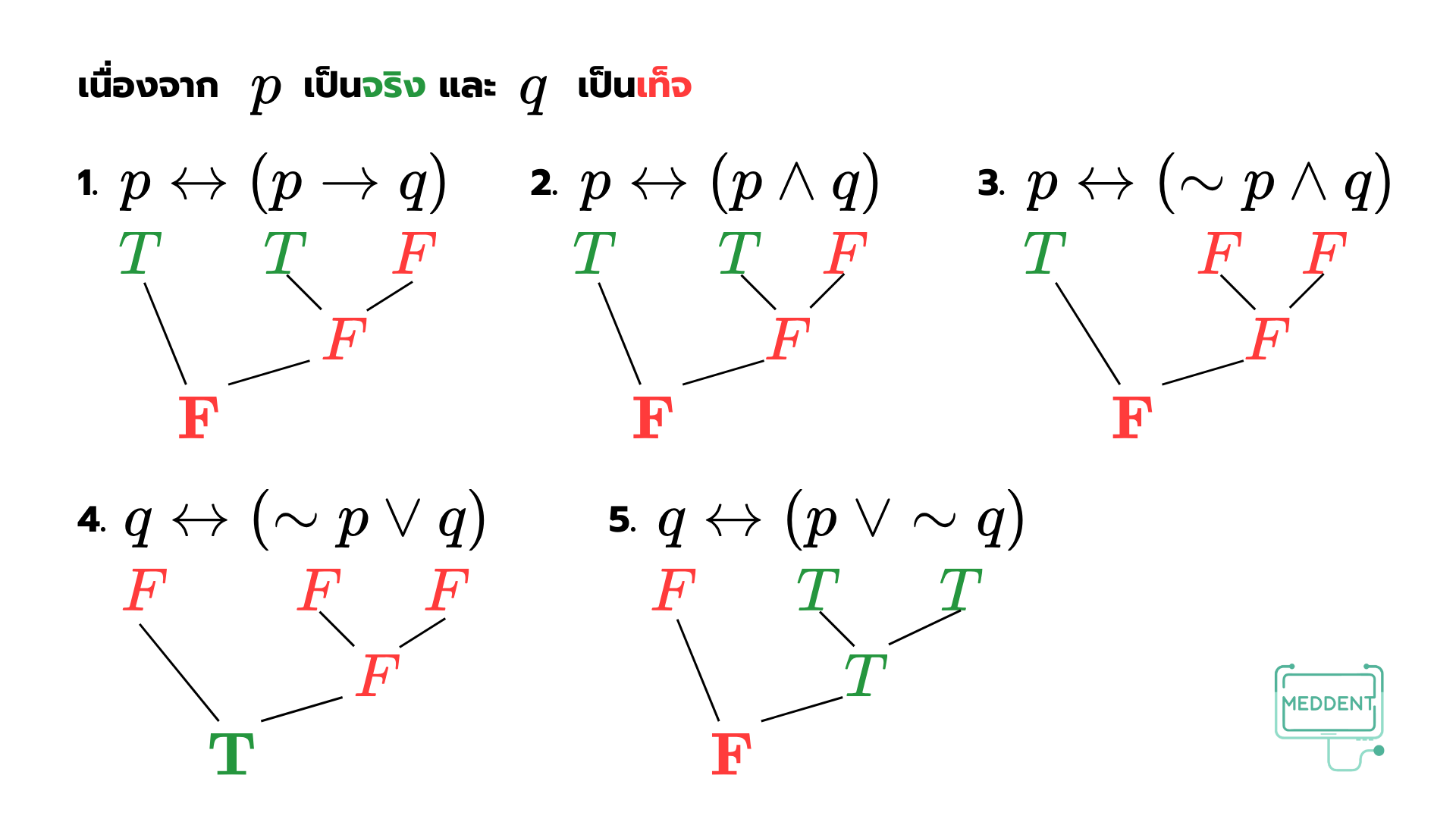
ตอบ ข้อ 4.
3. กำหนดให้ เป็นฟังก์ชันเชิงเส้น ถ้า และ แล้ว เท่ากับเท่าใด
(ข้อสอบ A-Level คณิตศาสตร์ประยุกต์ 2 รอบ มี.ค. 66)
วิธีทำ กำหนดให้ เป็นฟังก์ชันเชิงเส้น จะได้ว่า สำหรับทุกจำนวนจริง
(เมื่อ เป็นความชัน (slope) และ เป็นระยะตัดแกน )
เนื่องจาก และ จะได้ว่าความชัน
แทนค่าลงไปในสมการ จะได้ว่า นั่นคือ
ดังนั้น
ตอบ
4. เท่ากับเท่าใด
(ข้อสอบ วิชาสามัญคณิตศาสตร์ 2 รอบ มี.ค. 65)
วิธีทำ เนื่องจาก และ จะได้ว่า
ตอบ ข้อ 4.
5. ถ้า แล้วผลบวก พจน์แรกของลำดับนี้เท่ากับข้อใดต่อไปนี้
(ข้อสอบ วิชาสามัญคณิตศาสตร์ 2 รอบ ธ.ค. 59)
วิธีทำ เนื่องจาก และ
จากอนุกรมเลขคณิต
จะได้ว่า ผลบวก พจน์แรก คือ
ตอบ ข้อ 1.
6. ข้อสอบแบบเลือกคำตอบชุดหนึ่งมี ข้อ แต่ละข้อมี ตัวเลือก และมีตัวเลือกที่ถูกเพียงตัวเลือกเดียว
ถ้านายสบโชคเดาคำตอบแต่ละข้ออย่างสุ่ม ข้อละ ตัวเลือก ความน่าจะเป็นที่นายสบโชคจะเดาคำตอบผิดหมดทุกข้อเท่ากับข้อใดต่อไปนี้
(ข้อสอบ วิชาสามัญคณิตศาสตร์ 2 รอบ ธ.ค. 59)
วิธีทำ เนื่องจากข้อสอบชุดนี้มี ข้อ ในแต่ละข้อมี ตัวเลือก
จากหลักการคูณ จะได้ว่า คำตอบที่จะสามารถตอบได้แตกต่างกันทั้งหมดมี วิธี
และเหตุการณ์ที่จะเลือกตัวเลือกที่ผิดใน ข้อมี ตัวเลือก
จากหลักการคูณ จะได้ว่า คำตอบผิดที่สามารถตอบได้แตกต่างกันทั้งหมดมี วิธี
ดังนั้น ความน่าจะเป็นที่นายสบโชคจะเดาคำตอบผิดหมดทุกข้อเท่ากับ
ตอบ ข้อ 5.
7. ข้อมูลชุดใดต่อไปนี้ที่ มัธยฐาน ฐานนิยม
(ข้อสอบ วิชาสามัญคณิตศาสตร์ 2 รอบ มี.ค. 63)
วิธีทำ เนื่องจากมัธยฐานคือ ข้อมูลตัวที่อยู่ตรงกลาง ซึ่งสามารถหาได้โดยการนำจำนวนข้อมูลทั้งหมดบวกกับ แล้วนำจำนวนนี้ไปหารด้วย และฐานนิยม คือ ข้อมูลที่มีการซ้ำกันมากที่สุด ซึ่งมีได้สูงสุด ค่า โดยในแต่ละข้อสามารถหาได้ดังนี้
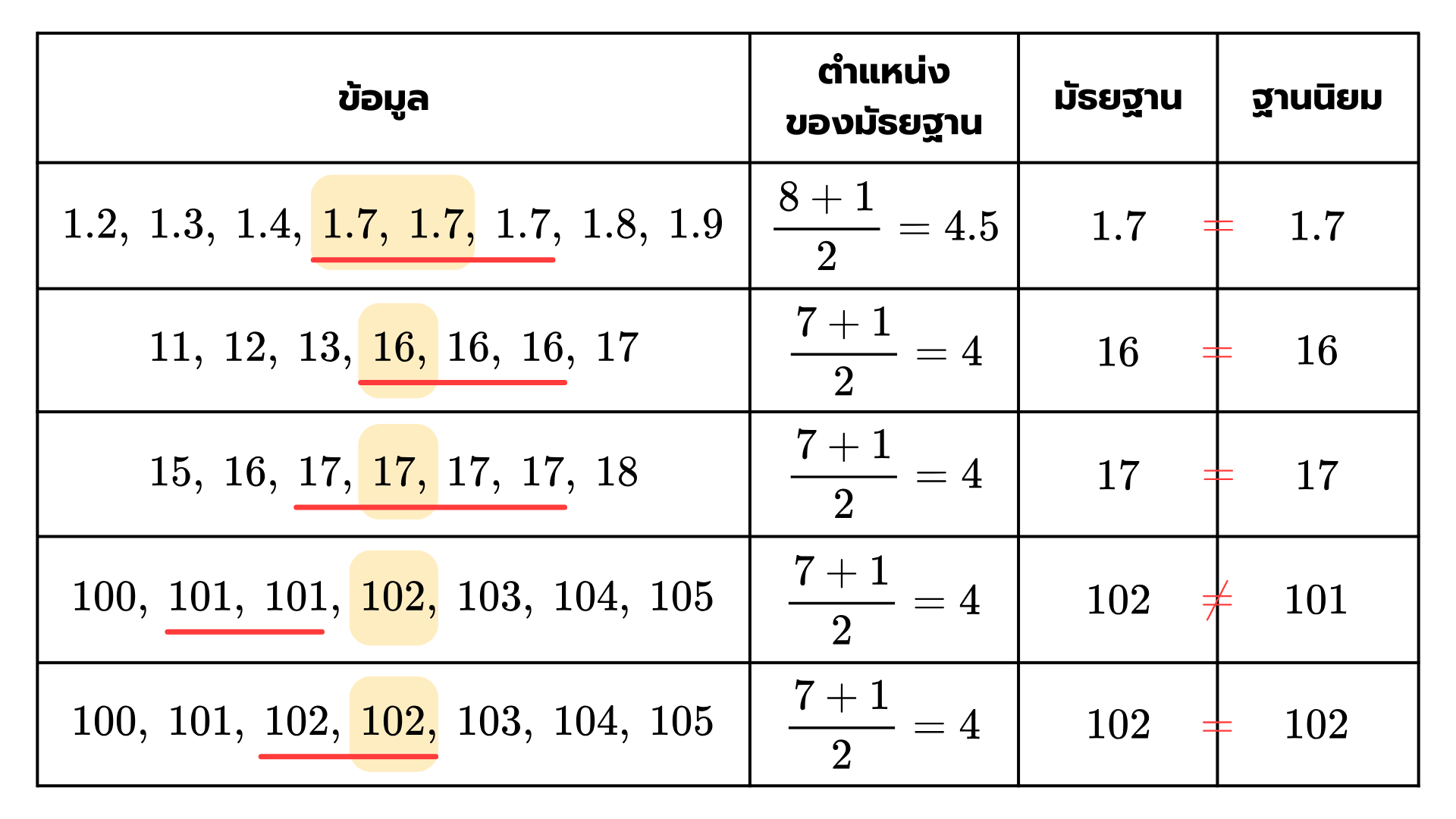
ตอบ ข้อ 4.
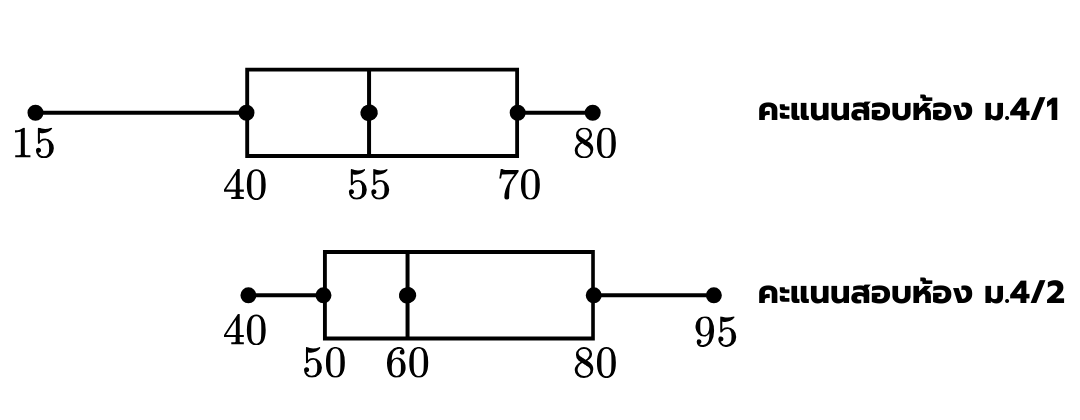
8. จากผลการสอบวิชาคณิตศาสตร์ของนักเรียนระดับชั้น ม.4 ซึ่งประกอบด้วยห้อง ม.4/1 และ ม.4/2 ที่มีจำนวนนักเรียนห้องละ คนเท่ากัน ได้ผลสรุปของคะแนนสอบเป็นแผนภาพกล่องดังนี้

ถ้าในการสอบครั้งนี้ครูให้ระดับคะแนน แก่ผู้ที่สอบได้คะแนนน้อยกว่า คะแนน และให้ระดับคะแนน แก่ผู้ที่สอบได้คะแนนมากกว่า คะแนน
แล้วพิจารณาข้อความต่อไปนี้
ก. พิสัยของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
ข. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
ค. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
ง. ค่าเฉลี่ยเลขคณิตของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
จำนวนข้อความที่ถูกต้อง เท่ากับข้อใดต่อไปนี้
- (ไม่มีข้อความใดถูก)
- มากกว่า
(ข้อสอบ วิชาสามัญคณิตศาสตร์ 2 รอบ ธ.ค. 59)
วิธีทำ เนื่องจากแผนภาพกล่องเป็นแผนภาพที่เกิดจากการแบ่งข้อมูลออกเป็น ส่วนที่เท่ากัน และนักเรียนห้อง ม.4/1 และ ม.4/2 ที่มีจำนวนนักเรียนห้องละ คนเท่ากัน แสดงว่าในแต่ละช่วงของนักเรียนในแต่ละห้องจะแบ่งเป็น คน
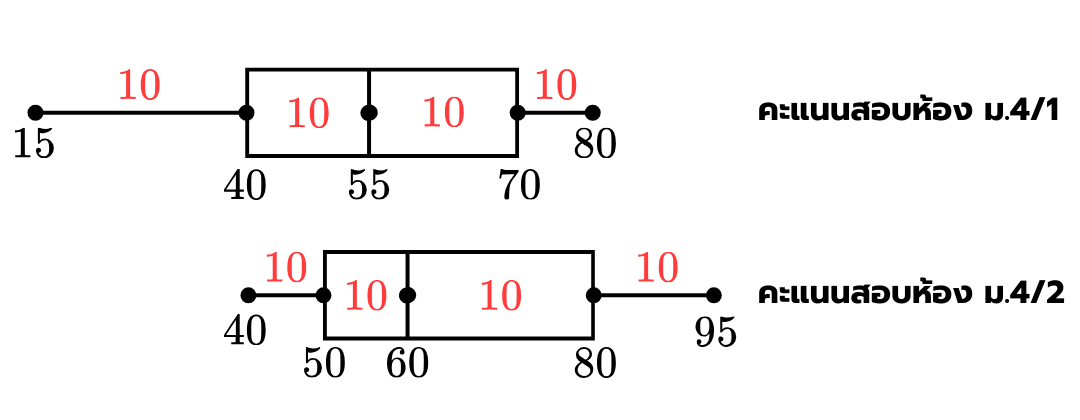
พิจารณาข้อความในแต่ละข้อต่อไปนี้
ก. พิสัยของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
เนื่องจากคะแนนต่ำสุดของนักเรียนทั้งระดับชั้นม.4 เท่ากับ คะแนน และคะแนนสูงสุดของนักเรียนทั้งระดับชั้น ม.4 เท่ากับ คะแนน จะได้ว่า พิสัย คะแนน ดังนั้น ข้อความนี้เป็นจริง
ข. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
เนื่องจากระดับคะแนน เป็นคนที่ได้คะแนนน้อยกว่า คะแนน ซึ่งมีทั้งหมด คน ซึ่งไม่เกิน คน ดังนั้น ข้อความนี้เป็นจริง
ค. นักเรียนชั้น ม.4 ที่ได้ระดับคะแนน มีไม่เกิน คน
เนื่องจากระดับคะแนน เป็นคนที่ได้คะแนนมากกว่า คะแนน ซึ่งมีทั้งหมด คน ซึ่งไม่เกิน คน ดังนั้น ข้อความนี้เป็นจริง
ง. ค่าเฉลี่ยเลขคณิตของคะแนนสอบของนักเรียนชั้น ม.4 เท่ากับ คะแนน
จากแผนภาพกล่องเป็นการแสดงการกระจายของข้อมูล ซึ่งจะไม่เห็นข้อมูลแต่ละตัวเป็นอะไรบ้าง จะได้ว่าไม่สามารถหาผลรวมของข้อมูลทั้งหมดได้ ทำให้ได้ว่า ค่าเฉลี่ยเลขคณิตหาไม่ได้ ดังนั้น ข้อความนี้เป็นเท็จ
จะเห็นว่า มีข้อถูกทั้งหมด ข้อ
ตอบ ข้อ 4.

