สวัสดีครับทุกคน วันนี้พี่แม็คจะพาไปทำความรู้จัก “แคลคูลัส
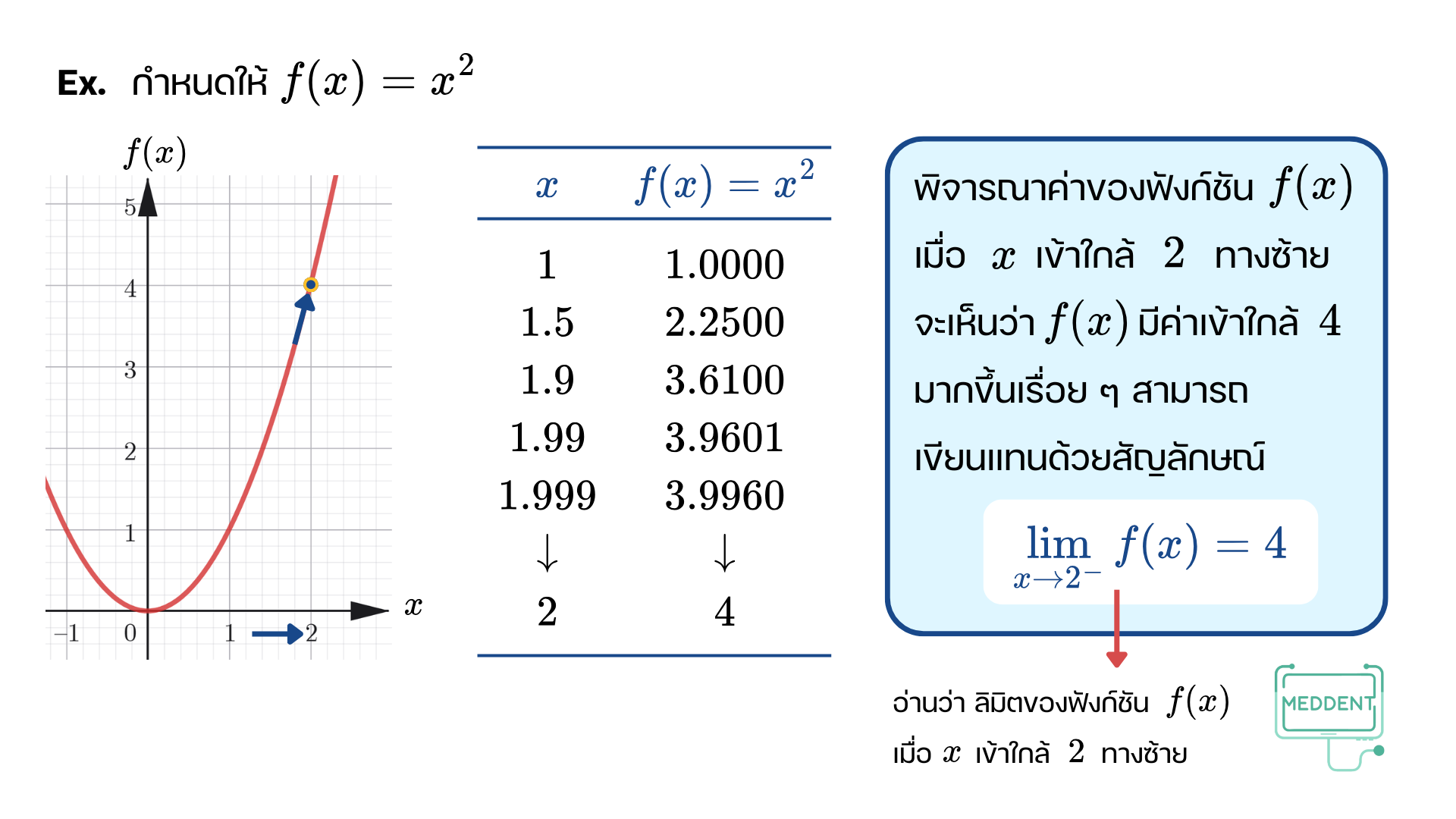
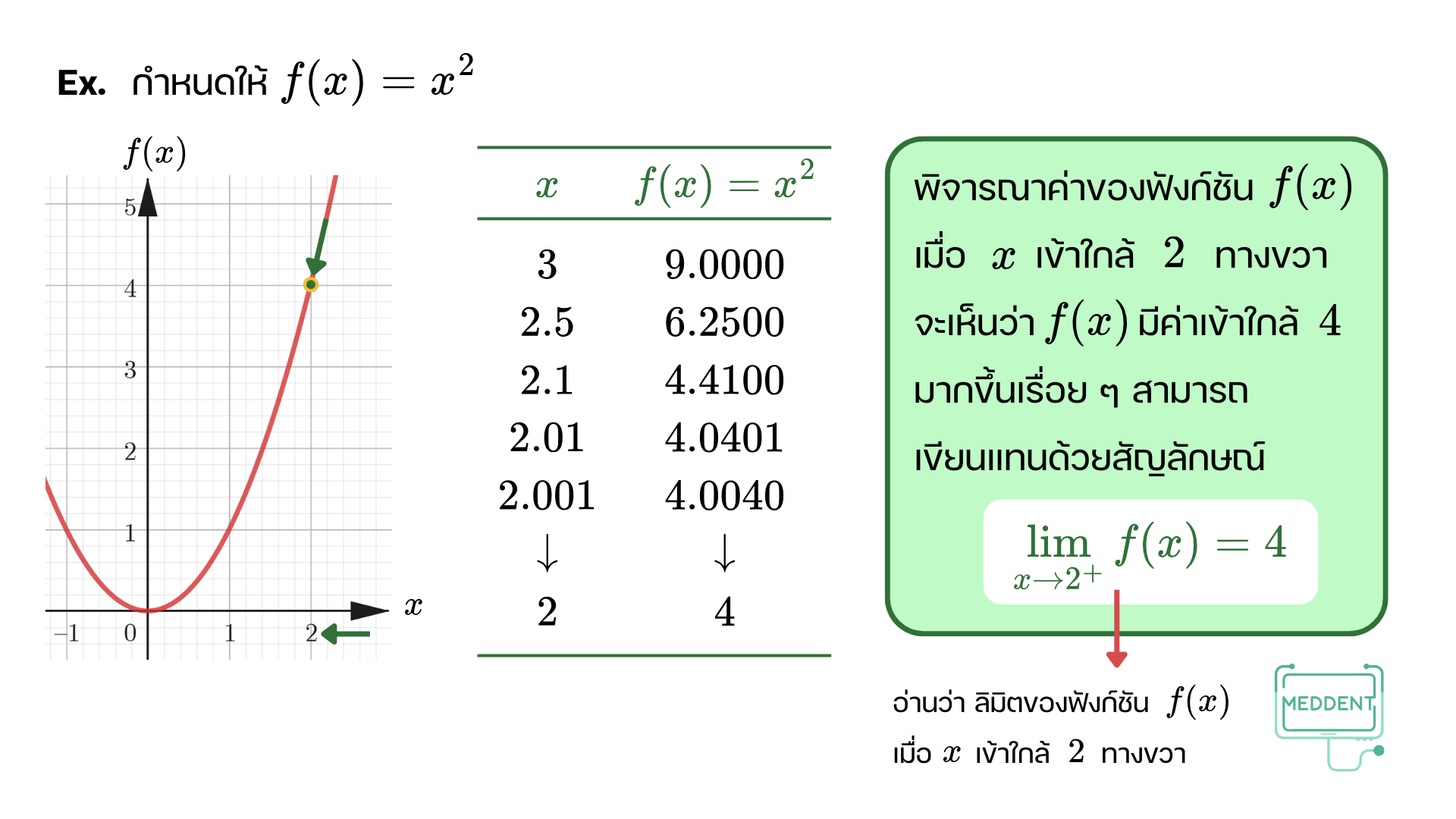
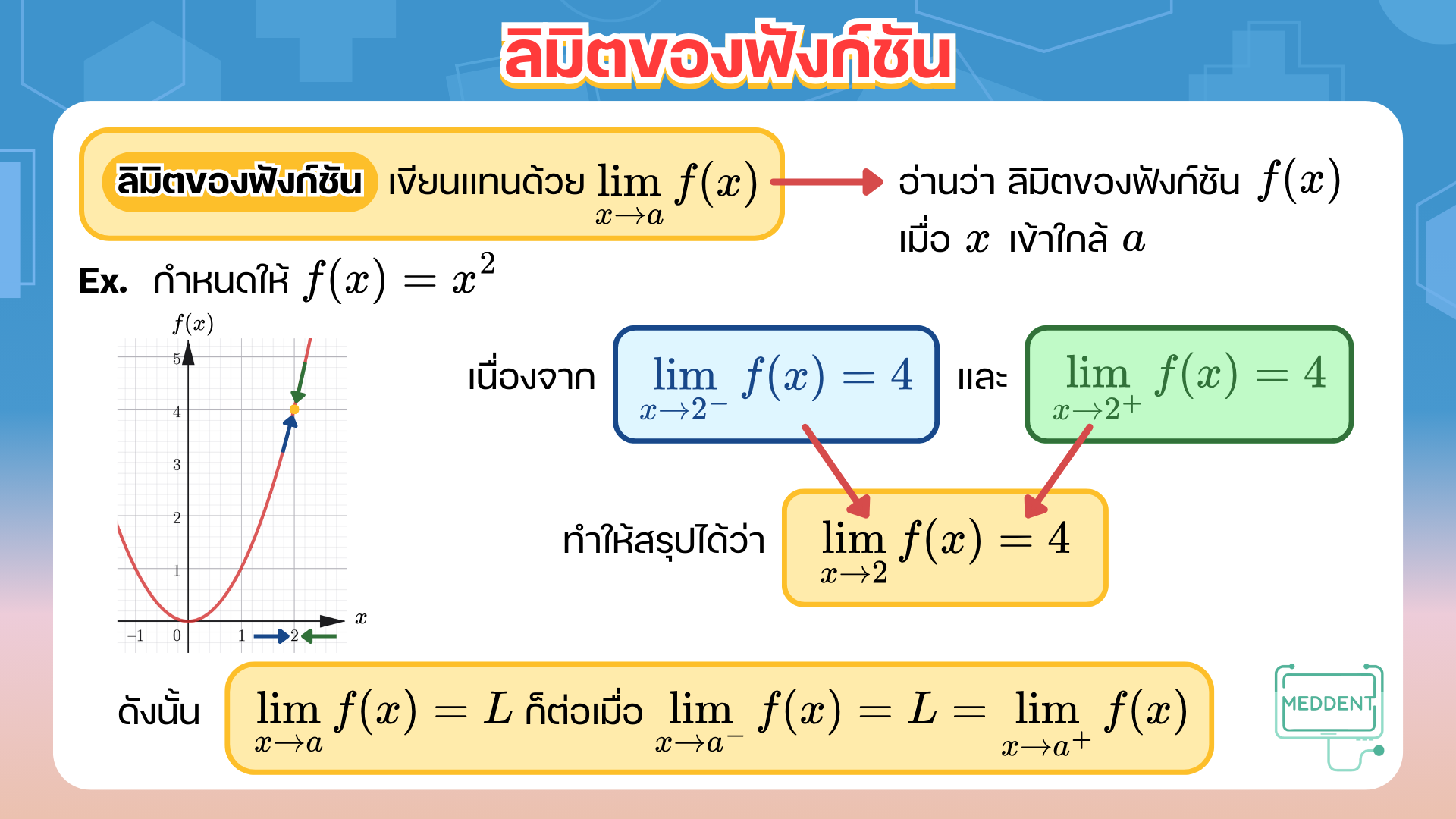
ก่อนอื่นพี่แม็คจะให้น้อง ๆ พิจารณาฟังก์ชัน y = x 2 y=x^2 y = x 2
จากตัวอย่างที่ผ่านมาทำให้เห็นว่า ถ้าลิมิตทางซ้ายของฟังก์ชัน f ( x ) f(x) f ( x ) x x x a a a f ( x ) f(x) f ( x ) x x x a a a lim x → a − f ( x ) = lim x → a + f ( x ) = L \displaystyle\lim_{x\to a^{-}}f(x) = \displaystyle\lim_{x\to a^{+}}f(x) = L x → a − lim f ( x ) = x → a + lim f ( x ) = L lim x → a f ( x ) = L \displaystyle\lim_{x\to a}f(x) = L x → a lim f ( x ) = L
แต่ถ้าลิมิตทางซ้ายของฟังก์ชัน f ( x ) f(x) f ( x ) x x x a a a f ( x ) f(x) f ( x ) x x x a a a lim x → a − f ( x ) ≠ lim x → a + f ( x ) \displaystyle\lim_{x\to a^{-}}f(x) \neq \displaystyle\lim_{x\to a^{+}}f(x) x → a − lim f ( x ) = x → a + lim f ( x ) f ( x ) f(x) f ( x ) x x x a a a
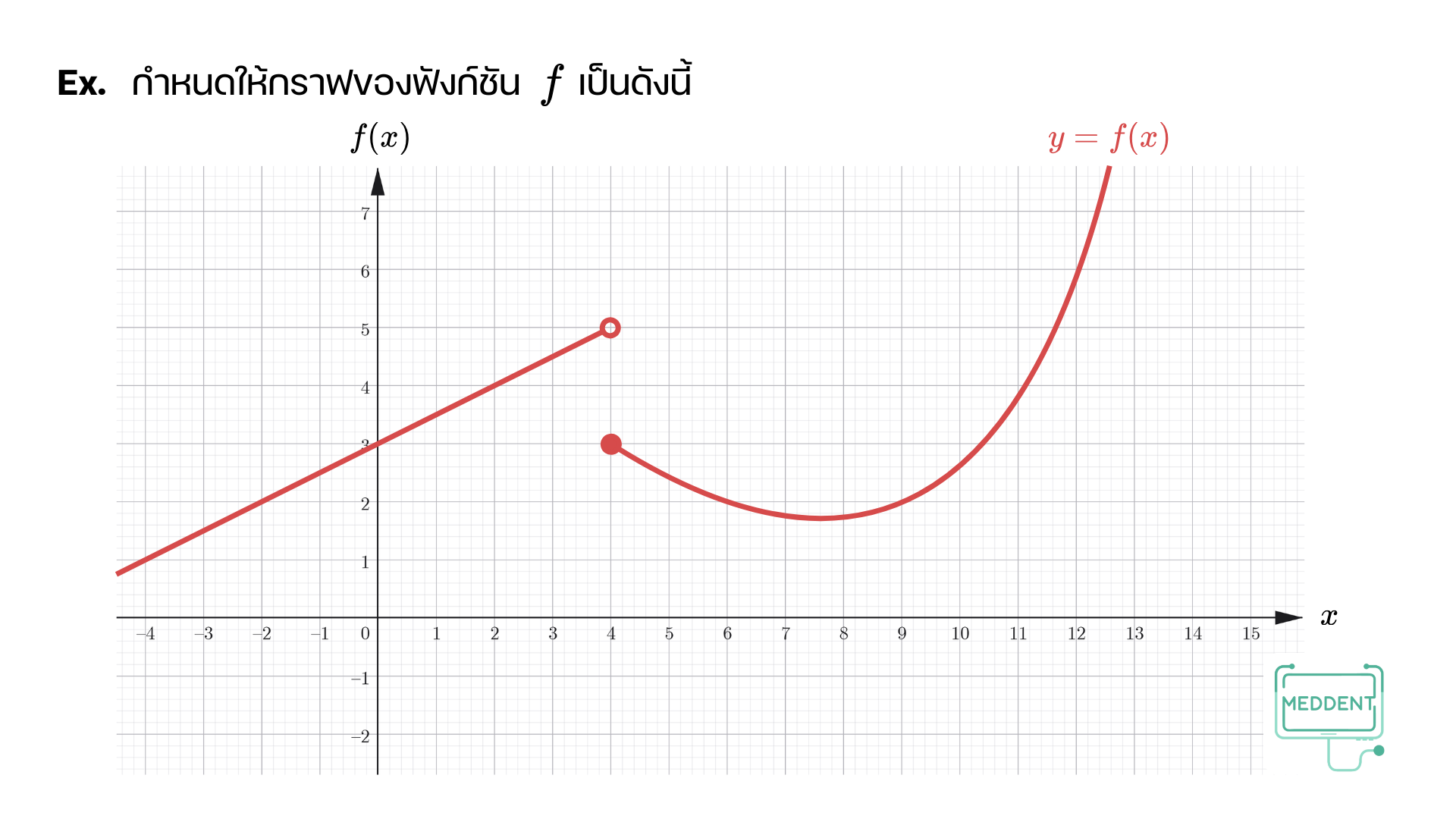
จงหา
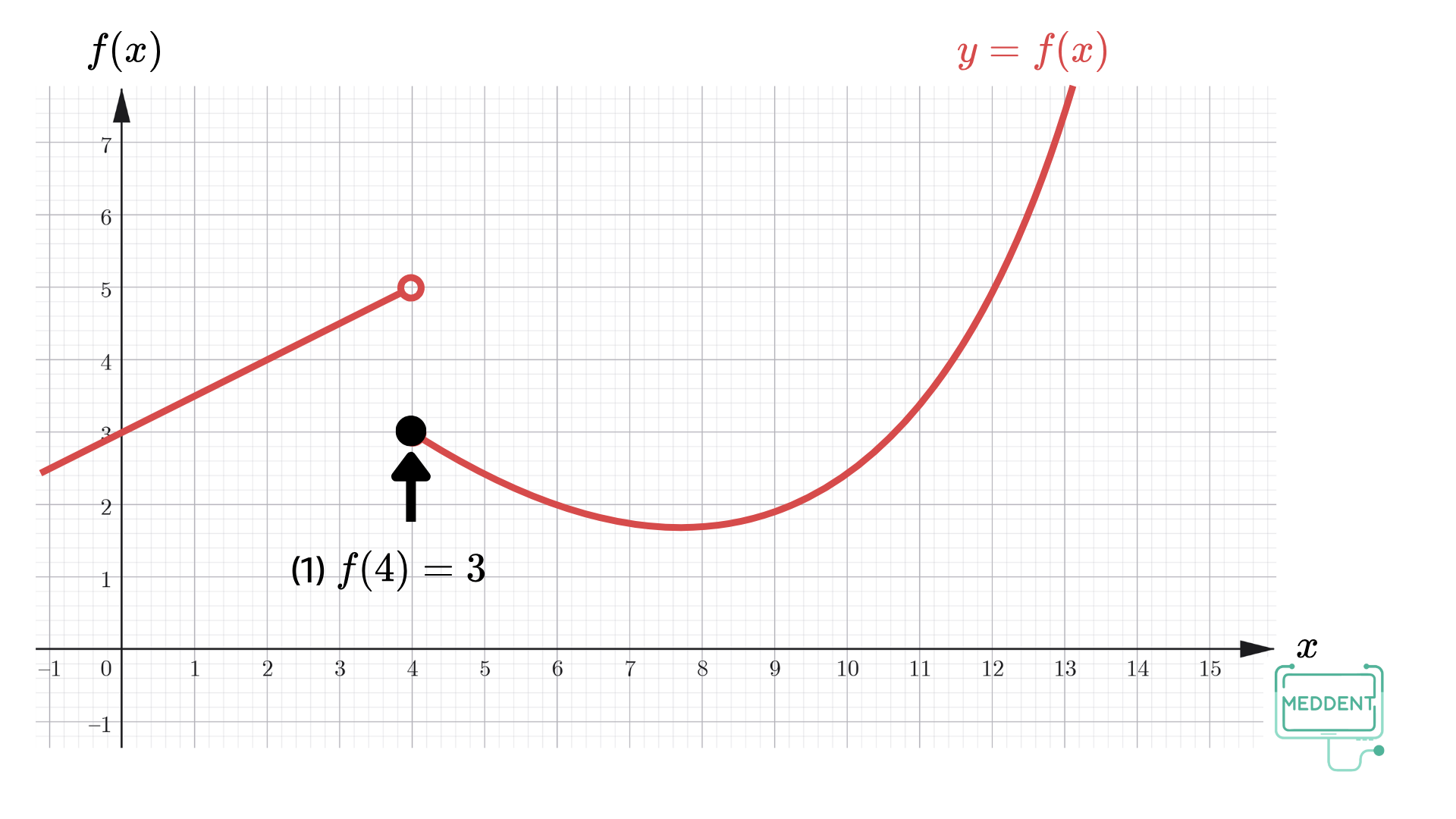
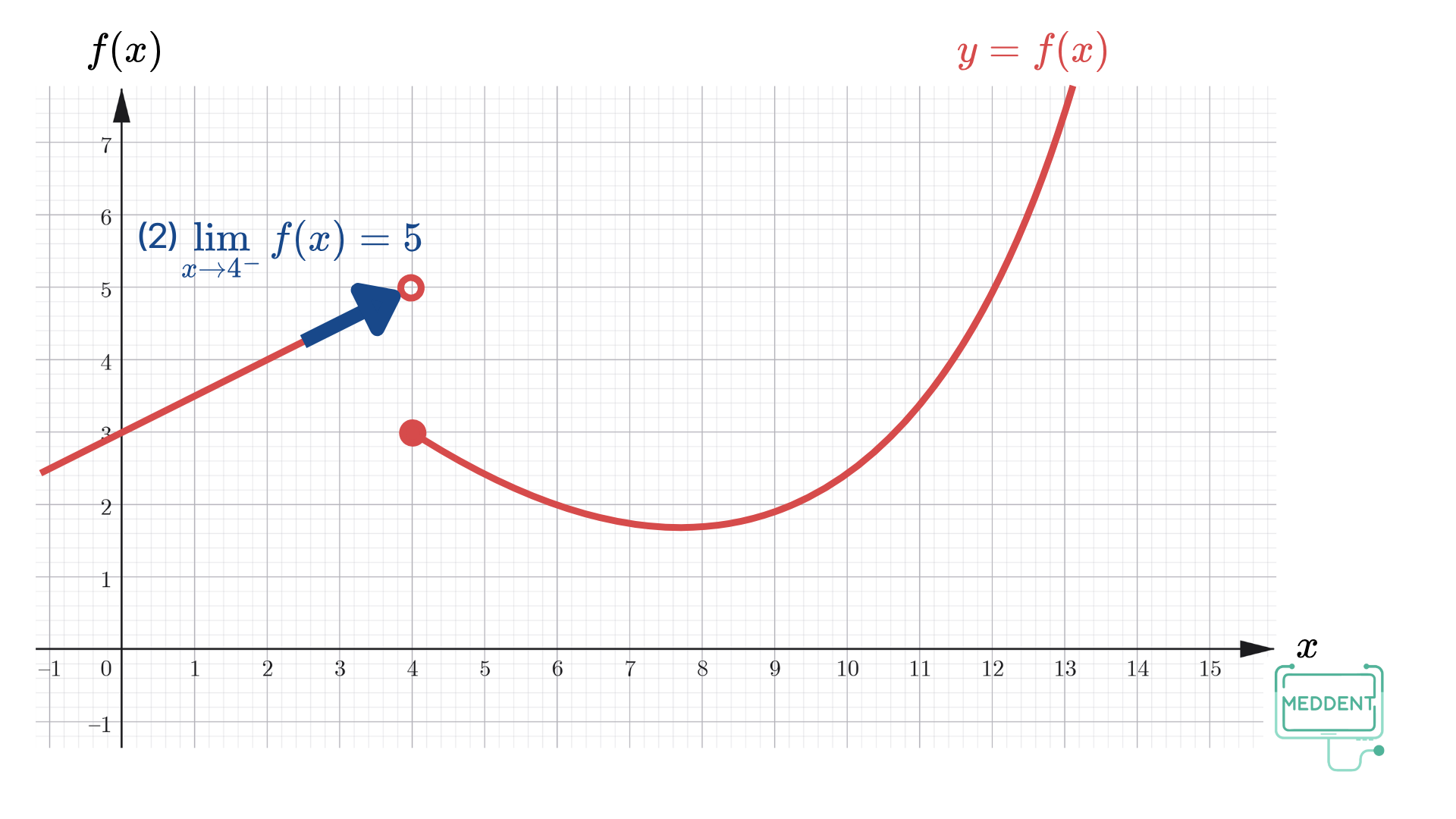
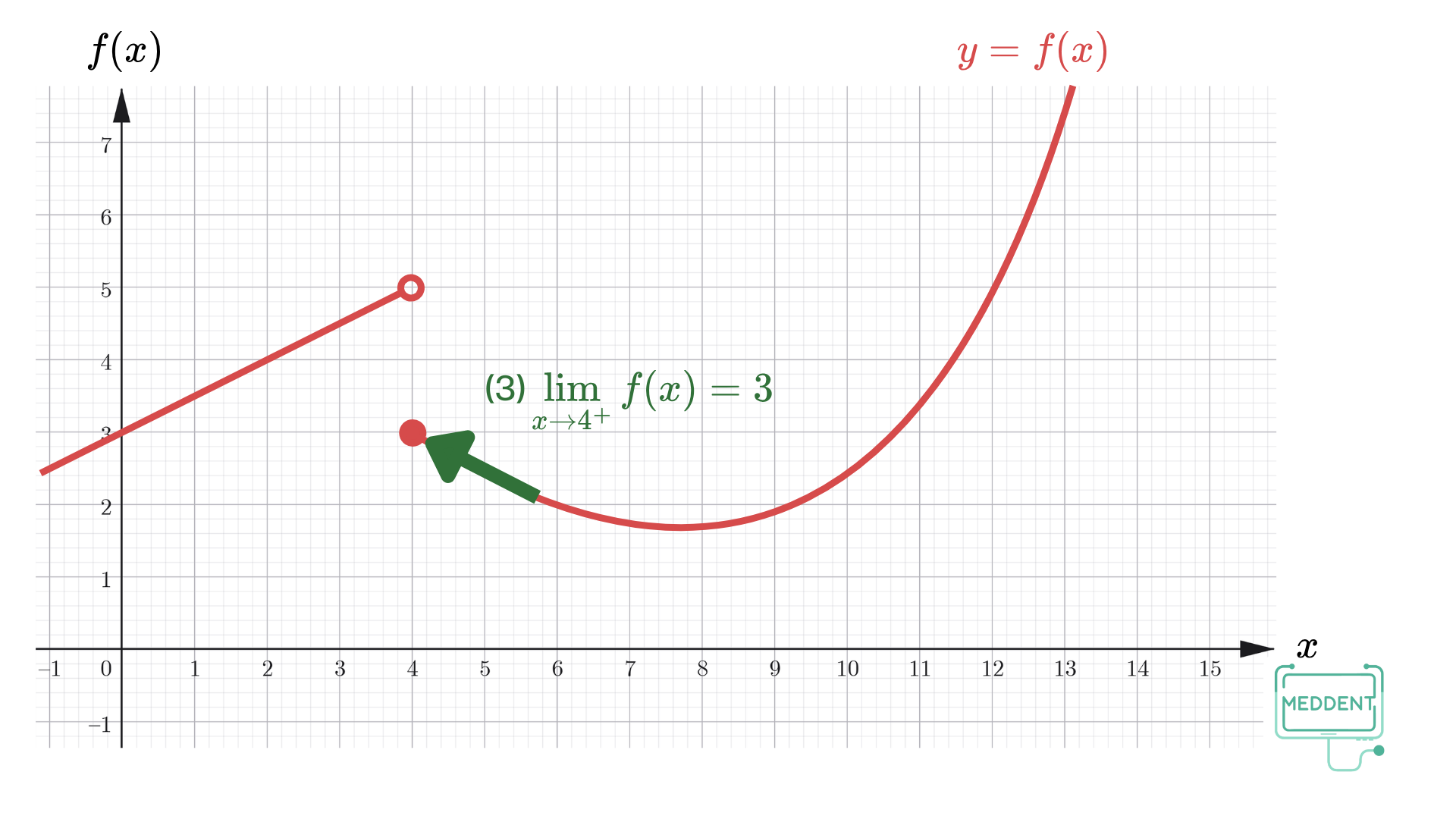
f ( 4 ) f(4) f ( 4 ) lim x → 4 − f ( x ) \displaystyle\lim_{x\to 4^-} f(x) x → 4 − lim f ( x ) lim x → 4 + f ( x ) \displaystyle\lim_{x\to 4^+} f(x) x → 4 + lim f ( x ) lim x → 4 f ( x ) \displaystyle\lim_{x\to 4} f(x) x → 4 lim f ( x ) วิธีทำ
f ( 4 ) = 3 f(4) = 3 f ( 4 ) = 3 lim x → 4 − f ( x ) = 5 \displaystyle\lim_{x\to 4^-} f(x) = 5 x → 4 − lim f ( x ) = 5 lim x → 4 + f ( x ) = 3 \displaystyle\lim_{x\to 4^+} f(x) = 3 x → 4 + lim f ( x ) = 3 เนื่องจาก lim x → 4 − f ( x ) = 5 \displaystyle\lim_{x\to 4^-} f(x) = 5 x → 4 − lim f ( x ) = 5 lim x → 4 + f ( x ) = 3 \displaystyle\lim_{x\to 4^+} f(x) = 3 x → 4 + lim f ( x ) = 3 lim x → 4 f ( x ) \displaystyle\lim_{x\to 4} f(x) x → 4 lim f ( x ) กำหนดให้ a a a L L L M M M f f f g g g โดยที่ lim x → a f ( x ) = L \displaystyle \lim_{x \to a} f(x) = L x → a lim f ( x ) = L lim x → a g ( x ) = M \displaystyle \lim_{x \to a} g(x) = M x → a lim g ( x ) = M
lim x → a c = c \displaystyle \lim_{x \to a} c = c x → a lim c = c c c c lim x → a x n = a n \displaystyle \lim_{x \to a} x^n = a^n x → a lim x n = a n n ∈ N n \in \mathbb{N} n ∈ N lim x → a c f ( x ) = c lim x → a f ( x ) = c L \displaystyle \lim_{x \to a} c f(x) = c \displaystyle \lim_{x \to a} f(x) = cL x → a lim c f ( x ) = c x → a lim f ( x ) = c L c c c lim x → a ( f ( x ) + g ( x ) ) = lim x → a f ( x ) + lim x → a g ( x ) = L + M \displaystyle \lim_{x \to a} (f(x) + g(x)) = \displaystyle \lim_{x \to a} f(x) + \displaystyle \lim_{x \to a} g(x) = L + M x → a lim ( f ( x ) + g ( x )) = x → a lim f ( x ) + x → a lim g ( x ) = L + M lim x → a ( f ( x ) − g ( x ) ) = lim x → a f ( x ) − lim x → a g ( x ) = L − M \displaystyle \lim_{x \to a} (f(x) - g(x)) = \displaystyle \lim_{x \to a} f(x) - \displaystyle \lim_{x \to a} g(x) = L - M x → a lim ( f ( x ) − g ( x )) = x → a lim f ( x ) − x → a lim g ( x ) = L − M lim x → a ( f ( x ) ⋅ g ( x ) ) = lim x → a f ( x ) ⋅ lim x → a g ( x ) = L ⋅ M \displaystyle \lim_{x \to a} (f(x) \cdot g(x)) = \displaystyle \lim_{x \to a} f(x) \cdot \displaystyle \lim_{x \to a} g(x) = L \cdot M x → a lim ( f ( x ) ⋅ g ( x )) = x → a lim f ( x ) ⋅ x → a lim g ( x ) = L ⋅ M lim x → a ( f ( x ) g ( x ) ) = lim x → a f ( x ) lim x → a g ( x ) = L M \displaystyle \lim_{x \to a} \left( \frac{f(x)}{g(x)} \right) = \frac{\displaystyle \lim_{x \to a} f(x)}{\displaystyle \lim_{x \to a} g(x)} = \frac{L}{M} x → a lim ( g ( x ) f ( x ) ) = x → a lim g ( x ) x → a lim f ( x ) = M L M ≠ 0 M \neq 0 M = 0 lim x → a ( f ( x ) ) n = ( lim x → a f ( x ) ) n = L n \displaystyle \lim_{x \to a} (f(x))^n = \left(\displaystyle \lim_{x \to a} f(x)\right)^n = L^n x → a lim ( f ( x ) ) n = ( x → a lim f ( x ) ) n = L n n ∈ N n \in \mathbb{N} n ∈ N lim x → a f ( x ) n = lim x → a f ( x ) n = L n \displaystyle \lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\displaystyle \lim_{x \to a} f(x)} = \sqrt[n]{L} x → a lim n f ( x ) = n x → a lim f ( x ) = n L n ∈ N − { 1 } n \in \mathbb{N}-\{1\} n ∈ N − { 1 } L n ∈ R \sqrt[n]{L} \in \mathbb{R} n L ∈ R Ex. จงหาค่าของ lim x → 2 ( 4 x 3 − 5 x + 7 ) \displaystyle \lim_{x \to 2} (4x^3 - 5x + 7) x → 2 lim ( 4 x 3 − 5 x + 7 ) วิธีทำ
lim x → 2 ( 4 x 3 − 5 x + 7 ) = lim x → 2 ( 4 x 3 ) − lim x → 2 ( 5 x ) + lim x → 2 ( 7 ) = 4 lim x → 2 ( x 3 ) − 5 lim x → 2 ( x ) + lim x → 2 ( 7 ) = 4 ( 2 3 ) − 5 ( 2 ) + 7 = 4 ( 8 ) − 10 + 7 = 32 − 10 + 7 = 29 \begin{align*}\displaystyle \lim_{x \to 2} (4x^3 - 5x + 7) &= \displaystyle \lim_{x \to 2} (4x^3) - \displaystyle \lim_{x \to 2}(5x) + \displaystyle \lim_{x \to 2} (7) \\ &= 4 \displaystyle \lim_{x \to 2} (x^3) - 5 \displaystyle \lim_{x \to 2} (x) + \displaystyle \lim_{x \to 2} (7) \\ &= 4(2^3) - 5(2) + 7 \\ &= 4(8) - 10 + 7 \\ &= 32 - 10 + 7 \\ &= 29 \end{align*} x → 2 lim ( 4 x 3 − 5 x + 7 ) = x → 2 lim ( 4 x 3 ) − x → 2 lim ( 5 x ) + x → 2 lim ( 7 ) = 4 x → 2 lim ( x 3 ) − 5 x → 2 lim ( x ) + x → 2 lim ( 7 ) = 4 ( 2 3 ) − 5 ( 2 ) + 7 = 4 ( 8 ) − 10 + 7 = 32 − 10 + 7 = 29
Ex. จงหาค่าของ lim x → 3 ( x 2 − 4 ) 2 x + 1 \displaystyle \lim_{x \to 3} \frac{(x^2 - 4)^2}{x + 1} x → 3 lim x + 1 ( x 2 − 4 ) 2 วิธีทำ
lim x → 3 ( x 2 − 4 ) 2 x + 1 = lim x → 3 ( ( x 2 − 4 ) 2 ) lim x → 3 ( x + 1 ) = ( lim x → 3 ( x 2 − 4 ) ) 2 lim x → 3 x + lim x → 3 1 = ( 3 2 − 4 ) 2 3 + 1 = ( 9 − 4 ) 2 4 = 5 2 4 = 25 4 \begin{align*}\displaystyle \lim_{x \to 3} \frac{(x^2 - 4)^2}{x + 1} &= \displaystyle \frac{\displaystyle \lim_{x \to 3} \left((x^2 - 4)^2\right)}{\displaystyle \lim_{x \to 3} (x + 1)} \\ &= \displaystyle \frac{\left(\displaystyle \lim_{x \to 3} (x^2 - 4)\right)^2}{\displaystyle \lim_{x \to 3} x + \displaystyle \lim_{x \to 3} 1} \\ &= \displaystyle \frac{(3^2 - 4)^2}{3 + 1} \\ &= \displaystyle \frac{(9 - 4)^2}{4} \\ &= \displaystyle \frac{5^2}{4} \\ &= \frac{25}{4} \end{align*} x → 3 lim x + 1 ( x 2 − 4 ) 2 = x → 3 lim ( x + 1 ) x → 3 lim ( ( x 2 − 4 ) 2 ) = x → 3 lim x + x → 3 lim 1 ( x → 3 lim ( x 2 − 4 ) ) 2 = 3 + 1 ( 3 2 − 4 ) 2 = 4 ( 9 − 4 ) 2 = 4 5 2 = 4 25
Ex. จงหาค่าของ lim x → 5 2 x 2 − 5 x − 5 \displaystyle \lim_{x \to 5} \sqrt{2x^2 - 5x - 5} x → 5 lim 2 x 2 − 5 x − 5 วิธีทำ
lim x → 5 2 x 2 − 5 x − 5 = lim x → 5 ( 2 x 2 − 5 x − 5 ) = lim x → 5 ( 2 x 2 ) − lim x → 5 ( 5 x ) − lim x → 5 ( 5 ) = 2 lim x → 5 ( x 2 ) − 5 lim x → 5 ( x ) − lim x → 5 ( 5 ) = 2 ( 5 2 ) − 5 ( 5 ) − 5 = 50 − 25 − 5 = 20 = 2 5 \begin{align*}\displaystyle \lim_{x \to 5} \sqrt{2x^2 - 5x - 5} &= \sqrt{\displaystyle \lim_{x \to 5} (2x^2 - 5x - 5)} \\ &= \sqrt{\displaystyle \lim_{x \to 5} (2x^2) -\displaystyle \lim_{x \to 5} (5x) - \displaystyle \lim_{x \to 5} (5) } \\ &= \sqrt{2 \displaystyle \lim_{x \to 5} (x^2) - 5 \displaystyle \lim_{x \to 5} (x) - \displaystyle \lim_{x \to 5} (5)} \\ &= \sqrt{2(5^2) - 5(5) - 5} \\ &= \sqrt{50 - 25 - 5} \\ &= \sqrt{20} \\ &= 2\sqrt{5} \end{align*} x → 5 lim 2 x 2 − 5 x − 5 = x → 5 lim ( 2 x 2 − 5 x − 5 ) = x → 5 lim ( 2 x 2 ) − x → 5 lim ( 5 x ) − x → 5 lim ( 5 ) = 2 x → 5 lim ( x 2 ) − 5 x → 5 lim ( x ) − x → 5 lim ( 5 ) = 2 ( 5 2 ) − 5 ( 5 ) − 5 = 50 − 25 − 5 = 20 = 2 5
จากทฤษฎีบทที่เกี่ยวกับลิมิตของฟังก์ชัน ข้อ (7) lim x → a ( f ( x ) g ( x ) ) = lim x → a f ( x ) lim x → a g ( x ) = L M \displaystyle \lim_{x \to a} \left( \frac{f(x)}{g(x)} \right) = \frac{\displaystyle \lim_{x \to a} f(x)}{\displaystyle \lim_{x \to a} g(x)} = \frac{L}{M} x → a lim ( g ( x ) f ( x ) ) = x → a lim g ( x ) x → a lim f ( x ) = M L M ≠ 0 M \neq 0 M = 0 แต่ถ้า M = 0 M=0 M = 0 lim x → a g ( x ) = 0 \displaystyle \lim_{x \to a} g(x)=0 x → a lim g ( x ) = 0
Ex. จงหาค่าของ lim x → 4 x 2 − 16 x − 4 \displaystyle \lim_{x \to 4} \frac{x^2 - 16}{x - 4} x → 4 lim x − 4 x 2 − 16 วิธีทำ เนื่องจาก lim x → 4 ( x − 4 ) = 0 \displaystyle \lim_{x \to 4} (x - 4) = 0 x → 4 lim ( x − 4 ) = 0
lim x → 4 x 2 − 16 x − 4 = lim x → 4 ( x − 4 ) ( x + 4 ) x − 4 = lim x → 4 ( x + 4 ) = 4 + 4 = 8 \begin{align*}\displaystyle \lim_{x \to 4} \frac{x^2 - 16}{x - 4} &= \displaystyle \lim_{x \to 4} \frac{(x-4)(x+4)}{x - 4} \\ &= \displaystyle \lim_{x \to 4} (x+4) \\ &= 4 + 4 \\ &= 8 \end{align*} x → 4 lim x − 4 x 2 − 16 = x → 4 lim x − 4 ( x − 4 ) ( x + 4 ) = x → 4 lim ( x + 4 ) = 4 + 4 = 8
Ex. จงหาค่าของ lim x → 0 x + 4 − 2 x \displaystyle \lim_{x \to 0} \frac{\sqrt{x+4} - 2}{x} x → 0 lim x x + 4 − 2 วิธีทำ เนื่องจาก lim x → 0 x = 0 \displaystyle \lim_{x \to 0} x = 0 x → 0 lim x = 0
lim x → 0 x + 4 − 2 x = lim x → 0 x + 4 − 2 x ⋅ x + 4 + 2 x + 4 + 2 = lim x → 0 ( x + 4 ) 2 − 2 2 x ( x + 4 + 2 ) = lim x → 0 x x ( x + 4 + 2 ) = lim x → 0 1 x + 4 + 2 = 1 0 + 4 + 2 = 1 2 + 2 = 1 4 \begin{align*}\displaystyle \lim_{x \to 0} \frac{\sqrt{x+4} - 2}{x} &= \displaystyle \lim_{x \to 0} \frac{\sqrt{x+4} - 2}{x} \cdot \frac{\sqrt{x+4} + 2}{\sqrt{x+4} + 2} \\ &= \displaystyle \lim_{x \to 0} \frac{\left(\sqrt{x+4}\right)^2 - 2^2}{x(\sqrt{x+4} + 2)} \\ &= \displaystyle \lim_{x \to 0} \frac{x}{x(\sqrt{x+4} + 2)} \\ &= \displaystyle \lim_{x \to 0} \frac{1}{\sqrt{x+4} + 2} \\ &= \displaystyle \frac{1}{\sqrt{0+4} + 2} \\ &= \displaystyle \frac{1}{2 + 2} \\ &= \frac{1}{4} \end{align*} x → 0 lim x x + 4 − 2 = x → 0 lim x x + 4 − 2 ⋅ x + 4 + 2 x + 4 + 2 = x → 0 lim x ( x + 4 + 2 ) ( x + 4 ) 2 − 2 2 = x → 0 lim x ( x + 4 + 2 ) x = x → 0 lim x + 4 + 2 1 = 0 + 4 + 2 1 = 2 + 2 1 = 4 1
ในเรื่องของความต่อเนื่องของฟังก์ชันเป็นแนวคิดที่ง่ายมากในแคลคูลัสครับ พี่แม็คจะสรุปให้น้อง ๆ ฟังอย่างคร่าวๆ เลยก็คือ ฟังก์ชันจะมีความต่อเนื่องที่จุดใดจุดหนึ่ง ก็ต่อเมื่อ เราสามารถลากเส้นกราฟผ่านจุดนั้นได้โดยไม่ต้องยกปากกานั่นเองครับ
เมื่อน้อง ๆ ลากปากกาไปตามกราฟจากฝั่งซ้ายมือไปยังฝั่งขวามือเรื่อย ๆ ที่เป็นกราฟเส้นตรง แต่เมื่อถึงที่จุด x = 4 x=4 x = 4 x = 4 x=4 x = 4 x = 4 x=4 x = 4
ต่อไปพี่แม็คจะให้น้อง ๆ พิจารณาว่า ฟังก์ชันจะมีความต่อเนื่องที่จุด x = a x=a x = a
Ex. กำหนดให้ฟังก์ชัน f f f
f ( x ) = { x 2 − 9 x − 3 เมื่อ x ≠ 3 6 เมื่อ x = 3 \begin{align*} f(x) = \begin{cases} \displaystyle \frac{x^2 - 9}{x - 3} & \text{เมื่อ } x \neq 3 \\ 6 & \text{เมื่อ } x = 3 \end{cases} \end{align*} f ( x ) = ⎩ ⎨ ⎧ x − 3 x 2 − 9 6 เมื่อ x = 3 เมื่อ x = 3
จงหาว่า ฟังก์ชัน f f f x = 3 x=3 x = 3 วิธีทำ ในการพิจารณาว่าฟังก์ชัน f f f x = 3 x=3 x = 3 3 3 3
ตรวจสอบว่า ค่าของฟังก์ชัน f ( 3 ) f(3) f ( 3 ) จากฟังก์ชัน f f f x = 3 x = 3 x = 3 f ( 3 ) f(3) f ( 3 ) 6 6 6 f ( 3 ) = 6 f(3) = 6 f ( 3 ) = 6 ตรวจสอบว่า ลิมิตของฟังก์ชัน lim x → 3 f ( x ) \displaystyle \lim_{x \to 3} f(x) x → 3 lim f ( x ) (เนื่องจากการหาค่าลิมิตเป็นการพิจารณาค่าที่อยู่รอบ ๆ จุด x = 3 x = 3 x = 3 (1) lim x → 3 + f ( x ) = lim x → 3 + x 2 − 9 x − 3 = lim x → 3 + ( x − 3 ) ( x + 3 ) x − 3 = lim x → 3 + ( x + 3 ) = 3 + 3 = 6 \displaystyle \lim_{x \to 3^+} f(x) = \displaystyle \lim_{x \to 3^+} \displaystyle \frac{x^2 - 9}{x - 3} = \displaystyle \lim_{x \to 3^+} \displaystyle \frac{(x-3)(x+3)}{x - 3} = \displaystyle \lim_{x \to 3^+} (x+3) = 3+3 = 6 x → 3 + lim f ( x ) = x → 3 + lim x − 3 x 2 − 9 = x → 3 + lim x − 3 ( x − 3 ) ( x + 3 ) = x → 3 + lim ( x + 3 ) = 3 + 3 = 6 (2) lim x → 3 − f ( x ) = lim x → 3 − x 2 − 9 x − 3 = lim x → 3 − ( x − 3 ) ( x + 3 ) x − 3 = lim x → 3 − ( x + 3 ) = 3 + 3 = 6 \displaystyle \lim_{x \to 3^-} f(x) = \displaystyle \lim_{x \to 3^-} \displaystyle \frac{x^2 - 9}{x - 3} = \displaystyle \lim_{x \to 3^-} \displaystyle \frac{(x-3)(x+3)}{x - 3} = \displaystyle \lim_{x \to 3^-} (x+3) = 3+3 = 6 x → 3 − lim f ( x ) = x → 3 − lim x − 3 x 2 − 9 = x → 3 − lim x − 3 ( x − 3 ) ( x + 3 ) = x → 3 − lim ( x + 3 ) = 3 + 3 = 6 จะได้ว่า lim x → 3 f ( x ) = 6 \displaystyle \lim_{x \to 3} f(x) = 6 x → 3 lim f ( x ) = 6 ตรวจสอบว่า f ( 3 ) = lim x → 3 f ( x ) f(3) = \displaystyle \lim_{x \to 3} f(x) f ( 3 ) = x → 3 lim f ( x ) จากข้อ 1. f ( 3 ) = 6 f(3) = 6 f ( 3 ) = 6 lim x → 3 f ( x ) = 6 \displaystyle \lim_{x \to 3} f(x) = 6 x → 3 lim f ( x ) = 6 จะได้ว่า f ( 3 ) = lim x → 3 f ( x ) f(3) = \displaystyle \lim_{x \to 3} f(x) f ( 3 ) = x → 3 lim f ( x ) ดังนั้น ฟังก์ชัน f f f x = 3 x=3 x = 3
Ex. กำหนดให้ฟังก์ชัน g g g
g ( x ) = { 2 x + 1 เมื่อ x ≤ 2 x 2 − 1 เมื่อ x > 2 \begin{align*} g(x) = \begin{cases} \displaystyle 2x + 1 & \text{เมื่อ } x \leq 2 \\ \displaystyle x^2 - 1 & \text{เมื่อ } x > 2 \end{cases} \end{align*} g ( x ) = { 2 x + 1 x 2 − 1 เมื่อ x ≤ 2 เมื่อ x > 2
จงหาว่า ฟังก์ชัน g g g x = 2 x=2 x = 2 วิธีทำ ในการพิจารณาว่าฟังก์ชัน g g g x = 2 x=2 x = 2 3 3 3
ตรวจสอบว่า ค่าของฟังก์ชัน g ( 2 ) g(2) g ( 2 ) จากฟังก์ชัน g g g x = 2 x = 2 x = 2 g ( 2 ) = 2 ( 2 ) + 1 = 5 g(2) = 2(2)+1 = 5 g ( 2 ) = 2 ( 2 ) + 1 = 5 ตรวจสอบว่า ลิมิตของฟังก์ชัน lim x → 2 g ( x ) \displaystyle \lim_{x \to 2} g(x) x → 2 lim g ( x ) (1) lim x → 2 + g ( x ) = lim x → 2 + 2 x + 1 = 2 ( 2 ) + 1 = 5 \displaystyle \lim_{x \to 2^+} g(x) = \displaystyle \lim_{x \to 2^+} 2x + 1 = 2(2)+1 = 5 x → 2 + lim g ( x ) = x → 2 + lim 2 x + 1 = 2 ( 2 ) + 1 = 5 (เนื่องจากการหาค่าลิมิตทางซ้ายจะพิจารณาค่าที่อยู่รอบ ๆ จุดที่ x < 2 x < 2 x < 2 (2) lim x → 2 − g ( x ) = lim x → 3 − x 2 − 1 = ( 2 ) 2 − 1 = 4 − 1 = 3 \displaystyle \lim_{x \to 2^-} g(x) = \displaystyle \lim_{x \to 3^-} x^2 - 1 = (2)^2-1 = 4-1=3 x → 2 − lim g ( x ) = x → 3 − lim x 2 − 1 = ( 2 ) 2 − 1 = 4 − 1 = 3 (เนื่องจากการหาค่าลิมิตทางขวาจะพิจารณาค่าที่อยู่รอบ ๆ จุดที่ x > 2 x > 2 x > 2 จะเห็นว่า lim x → 2 − g ( x ) ≠ lim x → 2 + g ( x ) \displaystyle \lim_{x \to 2^-} g(x) \neq \displaystyle \lim_{x \to 2^+} g(x) x → 2 − lim g ( x ) = x → 2 + lim g ( x ) ดังนั้น lim x → 2 g ( x ) \displaystyle \lim_{x \to 2} g(x) x → 2 lim g ( x )
ดังนั้น ฟังก์ชัน g g g x = 2 x=2 x = 2
โดยกระบวนการหาอนุพันธ์จะเรียกว่า Differentiation ในที่นี้บางครั้ง พี่แม็คอาจจะขอพูดย่อ ๆ ว่าเป็น การดิฟ
Ex. จงหาอนุพันธ์ของฟังก์ชัน f ( x ) = 2 x 2 − 4 x + 1 \displaystyle f(x) = 2x^2 - 4x + 1 f ( x ) = 2 x 2 − 4 x + 1 x = 5 \displaystyle x = 5 x = 5 วิธีทำ
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 [ 2 ( x + h ) 2 − 4 ( x + h ) + 1 ] − [ 2 x 2 − 4 x + 1 ] h = lim h → 0 [ 2 ( x 2 + 2 x h + h 2 ) − 4 ( x + h ) + 1 ] − [ 2 x 2 − 4 x + 1 ] h = lim h → 0 2 x 2 + 4 x h + 2 h 2 − 4 x − 4 h + 1 − 2 x 2 + 4 x − 1 h = lim h → 0 4 x h + 2 h 2 − 4 h h = lim h → 0 h ( 4 x + 2 h − 4 ) h = lim h → 0 ( 4 x + 2 h − 4 ) = 4 x + 2 ( 0 ) − 4 = 4 x − 4 \begin{align*}\displaystyle f^\prime(x) &= \lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \\ &= \lim_{h \to 0} \frac{[2(x+h)^2 - 4(x+h) + 1] - [2x^2 - 4x + 1]}{h} \\ &= \lim_{h \to 0} \frac{[2(x^2 + 2xh + h^2) - 4(x+h) + 1] - [2x^2 - 4x + 1]}{h} \\ &= \lim_{h \to 0} \frac{2x^2 + 4xh + 2h^2 - 4x - 4h + 1 - 2x^2 + 4x - 1}{h} \\ &= \lim_{h \to 0} \frac{4xh + 2h^2 - 4h}{h} \\ &= \lim_{h \to 0} \frac{h(4x + 2h - 4)}{h} \\ &= \lim_{h \to 0} (4x + 2h - 4) \\ &= 4x + 2(0) - 4 \\ &= 4x - 4 \end{align*} f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h [ 2 ( x + h ) 2 − 4 ( x + h ) + 1 ] − [ 2 x 2 − 4 x + 1 ] = h → 0 lim h [ 2 ( x 2 + 2 x h + h 2 ) − 4 ( x + h ) + 1 ] − [ 2 x 2 − 4 x + 1 ] = h → 0 lim h 2 x 2 + 4 x h + 2 h 2 − 4 x − 4 h + 1 − 2 x 2 + 4 x − 1 = h → 0 lim h 4 x h + 2 h 2 − 4 h = h → 0 lim h h ( 4 x + 2 h − 4 ) = h → 0 lim ( 4 x + 2 h − 4 ) = 4 x + 2 ( 0 ) − 4 = 4 x − 4
ดังนั้น อนุพันธ์ของฟังก์ชัน f f f x = 5 x=5 x = 5 f ′ ( 5 ) = 4 ( 5 ) − 4 = 20 − 4 = 16 f^\prime(5) = 4(5)-4 = 20-4 = 16 f ′ ( 5 ) = 4 ( 5 ) − 4 = 20 − 4 = 16
กำหนดให้ c c c f f f g g g x x x
ถ้า f ( x ) = c f(x) = c f ( x ) = c f ′ ( x ) = 0 f'(x) = 0 f ′ ( x ) = 0 Ex. ถ้า f ( x ) = 15 f(x) = 15 f ( x ) = 15 f ′ ( x ) = 0 f'(x) = 0 f ′ ( x ) = 0 ถ้า f ( x ) = x c f(x) = x^c f ( x ) = x c f ′ ( x ) = c x c − 1 f'(x) = cx^{c-1} f ′ ( x ) = c x c − 1 Ex. ถ้า f ( x ) = x 7 f(x) = x^7 f ( x ) = x 7 f ′ ( x ) = 7 x 7 − 1 = 7 x 6 f'(x)= 7x^{7-1} = 7x^6 f ′ ( x ) = 7 x 7 − 1 = 7 x 6 ( f + g ) ′ ( x ) = f ′ ( x ) + g ′ ( x ) (f+g)'(x) = f'(x) + g'(x) ( f + g ) ′ ( x ) = f ′ ( x ) + g ′ ( x ) ( f − g ) ′ ( x ) = f ′ ( x ) − g ′ ( x ) \displaystyle (f-g)'(x) = f'(x) - g'(x) ( f − g ) ′ ( x ) = f ′ ( x ) − g ′ ( x ) Ex. ถ้า f ( x ) = x 4 + x 3 − x f(x) = x^4 + x^3 - x f ( x ) = x 4 + x 3 − x f ′ ( x ) = 4 x 3 + 3 x 2 − 1 f'(x) = 4x^3 + 3x^2 - 1 f ′ ( x ) = 4 x 3 + 3 x 2 − 1 ( c f ) ′ ( x ) = c ( f ′ ( x ) ) (cf)'(x) = c(f'(x)) ( c f ) ′ ( x ) = c ( f ′ ( x )) Ex. ถ้า f ( x ) = 3 x 2 − 1 3 x 3 f(x) = 3x^2 - \displaystyle\frac{1}{3}x^3 f ( x ) = 3 x 2 − 3 1 x 3 f ′ ( x ) = 3 ⋅ 2 x 1 − 1 3 ⋅ 3 x 2 = 6 x + x 2 f'(x) = 3 \cdot 2x^1 - \displaystyle\frac{1}{3} \cdot 3x^2 = 6x+x^2 f ′ ( x ) = 3 ⋅ 2 x 1 − 3 1 ⋅ 3 x 2 = 6 x + x 2 ( f g ) ′ ( x ) = f ( x ) g ′ ( x ) + g ( x ) f ′ ( x ) (fg)'(x) = f(x)g'(x) + g(x)f'(x) ( f g ) ′ ( x ) = f ( x ) g ′ ( x ) + g ( x ) f ′ ( x ) Ex. ถ้า y = ( x 2 ) ( 3 x + 1 ) y = (x^2) (3x+1) y = ( x 2 ) ( 3 x + 1 ) y ′ = ( x 2 ) ⋅ ( d d x ( 3 x + 1 ) ) + ( 3 x + 1 ) ⋅ ( d d x ( x 2 ) ) = x 2 ⋅ 3 + ( 3 x + 1 ) ⋅ 2 x = 3 x 2 + 6 x 2 + 2 x = 9 x 2 + 2 x \begin{align*} y' &= (x^2) \cdot \left(\displaystyle\frac{d}{dx}(3x+1)\right) + (3x+1) \cdot \left(\displaystyle\frac{d}{dx}(x^2)\right) \\ &= x^2 \cdot 3 + (3x+1) \cdot 2x \\ &= 3x^2 + 6x^2 + 2x \\ &= 9x^2 + 2x \end{align*} y ′ = ( x 2 ) ⋅ ( d x d ( 3 x + 1 ) ) + ( 3 x + 1 ) ⋅ ( d x d ( x 2 ) ) = x 2 ⋅ 3 + ( 3 x + 1 ) ⋅ 2 x = 3 x 2 + 6 x 2 + 2 x = 9 x 2 + 2 x ( f g ) ′ ( x ) = g ( x ) f ′ ( x ) − f ( x ) g ′ ( x ) ( g ( x ) ) 2 \left( \displaystyle\frac{f}{g} \right)'(x) = \displaystyle\frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2} ( g f ) ′ ( x ) = ( g ( x ) ) 2 g ( x ) f ′ ( x ) − f ( x ) g ′ ( x ) Ex. ถ้า y = x − 5 x 3 \displaystyle y = \displaystyle\frac{x-5}{x^3} y = x 3 x − 5 y ′ = x 3 ⋅ ( d d x ( x − 5 ) ) − ( x − 5 ) ⋅ ( d d x ( x 3 ) ) ( x 3 ) 2 = x 3 ⋅ 1 − ( x − 5 ) ⋅ 3 x 2 x 6 = x 3 − 3 x 3 + 15 x 2 x 6 = − 2 x 3 + 15 x 2 x 6 = x 2 ( − 2 x + 15 ) x 6 = − 2 x + 15 x 4 \begin{align*} y' &= \displaystyle\frac{x^3 \cdot \left(\displaystyle\frac{d}{dx}(x-5)\right) - (x-5) \cdot \left(\displaystyle\frac{d}{dx} (x^3)\right)}{(x^3)^2} \\ &= \displaystyle\frac{x^3 \cdot 1 - (x-5) \cdot 3x^2}{x^6} \\ &= \displaystyle\frac{x^3 - 3x^3 +15x^2}{x^6} \\ &= \displaystyle\frac{-2x^3 +15x^2}{x^6} \\ &= \displaystyle\frac{x^2(-2x+15)}{x^6} \\ &= \displaystyle\frac{-2x+15}{x^4} \end{align*} y ′ = ( x 3 ) 2 x 3 ⋅ ( d x d ( x − 5 ) ) − ( x − 5 ) ⋅ ( d x d ( x 3 ) ) = x 6 x 3 ⋅ 1 − ( x − 5 ) ⋅ 3 x 2 = x 6 x 3 − 3 x 3 + 15 x 2 = x 6 − 2 x 3 + 15 x 2 = x 6 x 2 ( − 2 x + 15 ) = x 4 − 2 x + 15 ( f ∘ g ) ′ ( x ) = f ′ ( g ( x ) ) ⋅ g ′ ( x ) \displaystyle (f \circ g)'(x) = f'(g(x)) \cdot g'(x) ( f ∘ g ) ′ ( x ) = f ′ ( g ( x )) ⋅ g ′ ( x ) Ex. กำหนดให้ y = ( 3 x + 2 ) 5 y = (3x+2)^5 y = ( 3 x + 2 ) 5 y ′ y' y ′ คือ 3 x + 2 = u 3x+2 = u 3 x + 2 = u y = u 5 y = u^5 y = u 5 y ′ = 5 u 4 y' = 5u^4 y ′ = 5 u 4 แต่น้องอย่าลืมดิฟไส้ด้วยนั่นก็คือ d d x ( 3 x + 2 ) = 3 \displaystyle\frac{d}{dx}(3x+2) = 3 d x d ( 3 x + 2 ) = 3 ซึ่งถ้าเขียนวิธีทำจริงๆ จะเขียนได้ตามนี้เลยครับ y ′ = d d x ( 3 x + 2 ) 5 = 5 ( 3 x + 2 ) 4 ⋅ d d x ( 3 x + 2 ) = 5 ( 3 x + 2 ) 4 ⋅ 3 = 15 ( 3 x + 2 ) 4 \begin{align*} y' &= \displaystyle\frac{d}{dx} (3x+2)^5 \\ &= 5(3x+2)^4 \cdot \displaystyle\frac{d}{dx} (3x+2) \\ &= 5(3x+2)^4 \cdot 3 \\ &= 15(3x+2)^4 \end{align*} y ′ = d x d ( 3 x + 2 ) 5 = 5 ( 3 x + 2 ) 4 ⋅ d x d ( 3 x + 2 ) = 5 ( 3 x + 2 ) 4 ⋅ 3 = 15 ( 3 x + 2 ) 4 กำหนดให้ u = 3 x + 2 u=3x+2 u = 3 x + 2 y ′ = d d x u 5 = 5 u 4 ⋅ d d x u = 5 u 4 ⋅ d d x ( 3 x + 2 ) = 5 u 4 ⋅ 3 = 5 ( 3 x + 2 ) 4 ⋅ 3 = 15 ( 3 x + 2 ) 4 \begin{align*} y' &= \displaystyle\frac{d}{dx} u^5 \\ &= 5u^4 \cdot \displaystyle\frac{d}{dx} u \\ &= 5u^4 \cdot \displaystyle\frac{d}{dx} (3x+2) \\ &= 5u^4 \cdot 3 \\ &= 5(3x+2)^4 \cdot 3 \\ &= 15(3x+2)^4 \end{align*} y ′ = d x d u 5 = 5 u 4 ⋅ d x d u = 5 u 4 ⋅ d x d ( 3 x + 2 ) = 5 u 4 ⋅ 3 = 5 ( 3 x + 2 ) 4 ⋅ 3 = 15 ( 3 x + 2 ) 4 แต่วิธีการแสดงในแบบที่ 2 น้อง ๆ จะต้องประกาศตัวแปรก่อนทุกครั้ง และที่สำคัญ ตอนจบน้อง ๆ จะต้องเปลี่ยนตัวแปรกลับมาเป็นตัวแปร x x x กำหนดเส้นโค้งซึ่งเป็นกราฟของฟังก์ชัน y = f ( x ) y = f(x) y = f ( x )
ให้ P ( a , f ( a ) ) P(a, f(a)) P ( a , f ( a )) Q ( a + h , f ( a + h ) ) Q(a+h, f(a+h)) Q ( a + h , f ( a + h )) h ≠ 0 h \neq 0 h = 0
ความชันของเส้นตรงที่ผ่านจุด P P P Q Q Q f ( a + h ) − f ( a ) ( a + h ) − a = f ( a + h ) − f ( a ) h \displaystyle \frac{f(a+h)-f(a)}{(a+h)-a} = \frac{f(a+h)-f(a)}{h} ( a + h ) − a f ( a + h ) − f ( a ) = h f ( a + h ) − f ( a )
ความชันของเส้นโค้งที่จุด P P P lim h → 0 f ( a + h ) − f ( a ) h = f ′ ( a ) \displaystyle \lim_{h\to 0} \frac{f(a+h)-f(a)}{h} = f'(a) h → 0 lim h f ( a + h ) − f ( a ) = f ′ ( a )
Ex. จงหาสมการเส้นสัมผัสเส้นโค้ง y = x 2 + 5 x y = x^2 + 5x y = x 2 + 5 x x = 2 x = 2 x = 2 วิธีทำ ขั้นตอนการหาสมการเส้นสัมผัสเส้นโค้ง y = x 2 + 5 x y = x^2 + 5x y = x 2 + 5 x x = 2 x = 2 x = 2
หาความชันของเส้นโค้งที่ x = 2 x=2 x = 2 เนื่องจาก y ′ = 2 x + 5 y' = 2x+5 y ′ = 2 x + 5 x = 2 x=2 x = 2 m = y ′ ∣ x = 2 = 2 ( 2 ) + 5 = 9 m=\left. y'\right|_{x=2} = 2(2)+5 = 9 m = y ′ ∣ x = 2 = 2 ( 2 ) + 5 = 9 และเมื่อ x = 2 x=2 x = 2 y = x 2 + 5 x = ( 2 ) 2 + 5 ( 2 ) = 4 + 10 = 14 y = x^2 + 5x = (2)^2 + 5(2) = 4+10 =14 y = x 2 + 5 x = ( 2 ) 2 + 5 ( 2 ) = 4 + 10 = 14 หาสมการเส้นสัมผัสเส้นโค้ง y = x 2 + 5 x y = x^2 + 5x y = x 2 + 5 x x = 2 x = 2 x = 2 จากสมการ y − y 1 = m ( x − x 1 ) y - y_1 = m(x-x_1) y − y 1 = m ( x − x 1 ) y − 14 = 9 ( x − 2 ) y - 14 = 9(x-2) y − 14 = 9 ( x − 2 ) y = 9 x − 18 + 14 y = 9x - 18 + 14 y = 9 x − 18 + 14 ดังนั้น สมการเส้นสัมผัสเส้นโค้ง y = x 2 + 5 x y = x^2 + 5x y = x 2 + 5 x x = 2 x = 2 x = 2 y = 9 x − 4 y = 9x - 4 y = 9 x − 4 กระบวนการหาปฏิยานุพันธ์ของฟังก์ชัน จะเรียกว่า ปริพันธ์ หรืออินทิกรัล (integral)และเรียก ∫ f ( x ) d x \displaystyle\int f(x)\ dx ∫ f ( x ) d x ปริพันธ์ไม่จำกัดเขต (indefinite integral)
กำหนดให้ a a a k k k a ≠ 1 a \neq 1 a = 1 f f f g g g
∫ k d x = k x + c \displaystyle\int k \ dx = kx + c ∫ k d x = k x + c c c c Ex. ∫ 7 d x = 7 x + c \displaystyle\int 7 \ dx = 7x + c ∫ 7 d x = 7 x + c c c c ∫ x a d x = x a + 1 a + 1 + c \displaystyle\int x^a \ dx = \displaystyle\frac{x^{a+1}}{a+1} + c ∫ x a d x = a + 1 x a + 1 + c c c c Ex. ∫ x 6 d x = x 6 + 1 6 + 1 + c = x 7 7 + c \displaystyle\int x^6 \ dx = \displaystyle\frac{x^{6+1}}{6+1} + c = \displaystyle\frac{x^7}{7} + c ∫ x 6 d x = 6 + 1 x 6 + 1 + c = 7 x 7 + c c c c ∫ k f ( x ) d x = k ∫ f ( x ) d x \displaystyle\int kf(x) \ dx = k\displaystyle\int f(x) \ dx ∫ k f ( x ) d x = k ∫ f ( x ) d x ∫ f ( x ) + g ( x ) d x = ∫ f ( x ) d x + ∫ g ( x ) d x \displaystyle\int f(x)+g(x) \ dx = \displaystyle\int f(x) \ dx + \displaystyle\int g(x) \ dx ∫ f ( x ) + g ( x ) d x = ∫ f ( x ) d x + ∫ g ( x ) d x ∫ f ( x ) − g ( x ) d x = ∫ f ( x ) d x − ∫ g ( x ) d x \displaystyle\int f(x)-g(x) \ dx = \displaystyle\int f(x) \ dx - \displaystyle\int g(x) \ dx ∫ f ( x ) − g ( x ) d x = ∫ f ( x ) d x − ∫ g ( x ) d x Ex. จงหาค่าของ ∫ 4 x + 1 3 x 2 d x \displaystyle\int 4x+ \frac{1}{3}x^2 \ dx ∫ 4 x + 3 1 x 2 d x วิธีทำ ∫ 4 x + 1 3 x 2 d x = ∫ 4 x d x + ∫ 1 3 x 2 d x = 4 ∫ x d x + 1 3 ∫ x 2 d x = 4 [ x 1 + 1 1 + 1 + c 1 ] + 4 [ x 2 + 1 2 + 1 + c 2 ] เมื่อ c 1 , c 2 เป็นจำนวนจริง = 4 [ x 2 2 + c 1 ] + 1 3 [ x 3 3 + c 2 ] เมื่อ c 1 , c 2 เป็นจำนวนจริง = 2 x 2 + x 3 9 + C เมื่อ C = 4 c 1 + 1 3 c 2 \begin{align*} \displaystyle\int 4x + \frac{1}{3}x^2 \ dx &= \displaystyle\int 4x \ dx+ \displaystyle\int\frac{1}{3}x^2 \ dx \\ &= \displaystyle 4 \int x \ dx+ \displaystyle\frac{1}{3}\int x^2 \ dx \\ &= \displaystyle 4 \left[ \displaystyle\frac{x^{1+1}}{1+1} + c_1 \right] + \displaystyle 4 \left[ \displaystyle\frac{x^{2+1}}{2+1} + c_2 \right] &\text{เมื่อ } c_1,c_2 \text{ เป็นจำนวนจริง} \\ &= \displaystyle 4 \left[ \displaystyle\frac{x^{2}}{2} + c_1 \right] + \displaystyle\frac{1}{3}\left[ \displaystyle\frac{x^{3}}{3} + c_2\right] &\text{เมื่อ } c_1,c_2 \text{ เป็นจำนวนจริง} \\ &= \displaystyle 2x^2 + \displaystyle\frac{x^3}{9} + C &\text{เมื่อ } C = 4c_1+ \frac{1}{3}c_2 \end{align*} ∫ 4 x + 3 1 x 2 d x = ∫ 4 x d x + ∫ 3 1 x 2 d x = 4 ∫ x d x + 3 1 ∫ x 2 d x = 4 [ 1 + 1 x 1 + 1 + c 1 ] + 4 [ 2 + 1 x 2 + 1 + c 2 ] = 4 [ 2 x 2 + c 1 ] + 3 1 [ 3 x 3 + c 2 ] = 2 x 2 + 9 x 3 + C เมื่อ c 1 , c 2 เป็นจำนวนจริง เมื่อ c 1 , c 2 เป็นจำนวนจริง เมื่อ C = 4 c 1 + 3 1 c 2 Ex. จงหาค่าของ ∫ 4 x − 6 x 2 3 d x \displaystyle\int 4\sqrt{x} - \frac{6}{\sqrt[3]{x^2}} dx ∫ 4 x − 3 x 2 6 d x วิธีทำ ∫ 4 x − 6 x 2 3 d x = ∫ ( 4 x 1 2 − 6 x − 2 3 ) d x = 4 x 1 2 + 1 1 2 + 1 − 6 x − 2 3 + 1 − 2 3 + 1 + C เมื่อ C เป็นจำนวนจริง = 4 x 3 2 3 2 − 6 x 1 3 1 3 + C เมื่อ C เป็นจำนวนจริง = 4 ⋅ 2 3 x 3 2 − 6 ⋅ 3 x 1 3 + C เมื่อ C เป็นจำนวนจริง = 8 3 x 3 2 − 18 x 1 3 + C เมื่อ C เป็นจำนวนจริง \begin{align*} \displaystyle \int 4\sqrt{x} - \frac{6}{\sqrt[3]{x^2}} dx &= \displaystyle \int (4x^{\frac{1}{2}} - 6x^{-\frac{2}{3}}) dx \\ &= 4 \displaystyle \frac{x^{\frac{1}{2} + 1}}{\frac{1}{2} + 1} - 6 \displaystyle \frac{x^{-\frac{2}{3} + 1}}{-\frac{2}{3} + 1} + C &\text{เมื่อ } C \text{ เป็นจำนวนจริง} \\ &= 4 \displaystyle \frac{x^{\frac{3}{2}}}{\frac{3}{2}} - 6 \displaystyle \frac{x^{\frac{1}{3}}}{\frac{1}{3}} + C &\text{เมื่อ } C \text{ เป็นจำนวนจริง} \\ &= 4 \cdot \frac{2}{3} x^{\frac{3}{2}} - 6 \cdot 3 x^{\frac{1}{3}} + C &\text{เมื่อ } C \text{ เป็นจำนวนจริง} \\ &= \displaystyle\frac{8}{3} x^{\frac{3}{2}} - 18 x^{\frac{1}{3}} + C &\text{เมื่อ } C \text{ เป็นจำนวนจริง} \end{align*} ∫ 4 x − 3 x 2 6 d x = ∫ ( 4 x 2 1 − 6 x − 3 2 ) d x = 4 2 1 + 1 x 2 1 + 1 − 6 − 3 2 + 1 x − 3 2 + 1 + C = 4 2 3 x 2 3 − 6 3 1 x 3 1 + C = 4 ⋅ 3 2 x 2 3 − 6 ⋅ 3 x 3 1 + C = 3 8 x 2 3 − 18 x 3 1 + C เมื่อ C เป็นจำนวนจริง เมื่อ C เป็นจำนวนจริง เมื่อ C เป็นจำนวนจริง เมื่อ C เป็นจำนวนจริง ปริพันธ์จำกัดเขต (definite integral) ของฟังก์ชัน f f f [ a , b ] [a,b] [ a , b ] ∫ a b f ( x ) d x \displaystyle\int\limits_a^b f(x)\ dx a ∫ b f ( x ) d x เรียก a a a ลิมิตล่าง (lower limit) ของปริพันธ์ และเรียก b b b ลิมิตบน (upper limit) ของปริพันธ์
การหาปริพันธ์จำกัดเขต ∫ a b f ( x ) d x \displaystyle\int\limits_a^b f(x)\ dx a ∫ b f ( x ) d x
หา ∫ f ( x ) d x \displaystyle\int f(x)\ dx ∫ f ( x ) d x หาค่าของ F ( b ) − F ( a ) F(b)-F(a) F ( b ) − F ( a ) F ( x ) ∣ a b \left. F(x)\right|_a^b F ( x ) ∣ a b จะได้ว่า ∫ a b f ( x ) d x = F ( x ) ∣ a b = F ( b ) − F ( a ) \displaystyle\int\limits_a^b f(x)\ dx = \left. F(x)\right|_a^b = F(b)-F(a) a ∫ b f ( x ) d x = F ( x ) ∣ a b = F ( b ) − F ( a ) Ex. จงหาค่าของ ∫ 1 3 ( 2 x + 1 ) d x \displaystyle \int\limits_{1}^{3} (2x + 1) dx 1 ∫ 3 ( 2 x + 1 ) d x วิธีทำ
∫ 1 3 ( 2 x + 1 ) d x = [ 2 ⋅ x 2 2 + x ] 1 3 = [ x 2 + x ] 1 3 = ( 3 2 + 3 ) − ( 1 2 + 1 ) = 12 − 2 = 10 \begin{align*} \displaystyle \int\limits_{1}^{3} (2x + 1) dx &= \left[ 2 \cdot \frac{x^2}{2} + x \right]_{1}^{3} \\ &= \left[ x^2 + x \right]_{1}^{3} \\ &= (3^2 + 3) - (1^2 + 1) \\ &= 12 - 2 \\ &= 10 \end{align*} 1 ∫ 3 ( 2 x + 1 ) d x = [ 2 ⋅ 2 x 2 + x ] 1 3 = [ x 2 + x ] 1 3 = ( 3 2 + 3 ) − ( 1 2 + 1 ) = 12 − 2 = 10
Ex. จงหาค่าของ ∫ 1 2 ( 3 x 2 − 4 x 2 ) d x \displaystyle \int\limits_{1}^{2} \left( 3x^2 - \frac{4}{x^2} \right) dx 1 ∫ 2 ( 3 x 2 − x 2 4 ) d x วิธีทำ
∫ 1 2 ( 3 x 2 − 4 x 2 ) d x = ∫ 1 2 ( 3 x 2 − 4 x − 2 ) d x = [ 3 ⋅ x 3 3 − 4 ⋅ x − 1 − 1 ] 1 2 = [ x 3 + 4 x − 1 ] 1 2 = [ x 3 + 4 x ] 1 2 = ( 2 3 + 4 2 ) − ( 1 3 + 4 1 ) = ( 8 + 2 ) − ( 1 + 4 ) = 10 − 5 = 5 \begin{align*} \displaystyle \int\limits_{1}^{2} \left( 3x^2 - \frac{4}{x^2} \right) dx &= \displaystyle \int\limits_{1}^{2} (3x^2 - 4x^{-2}) dx \\ &= \left[ 3 \cdot \frac{x^{3}}{3} - 4 \cdot \frac{x^{-1}}{-1} \right]_{1}^{2} \\ &= \left[ x^3 + 4x^{-1} \right]_{1}^{2} \\ &= \left[ x^3 + \frac{4}{x} \right]_{1}^{2} \\ &= \left( 2^3 + \frac{4}{2} \right) - \left( 1^3 + \frac{4}{1} \right) \\ &= (8 + 2) - (1 + 4) \\ &= 10 - 5 \\ &= 5 \end{align*} 1 ∫ 2 ( 3 x 2 − x 2 4 ) d x = 1 ∫ 2 ( 3 x 2 − 4 x − 2 ) d x = [ 3 ⋅ 3 x 3 − 4 ⋅ − 1 x − 1 ] 1 2 = [ x 3 + 4 x − 1 ] 1 2 = [ x 3 + x 4 ] 1 2 = ( 2 3 + 2 4 ) − ( 1 3 + 1 4 ) = ( 8 + 2 ) − ( 1 + 4 ) = 10 − 5 = 5
Ex. จงหาค่าของ ∫ 4 9 ( 1 x ) d x \displaystyle \int\limits_{4}^{9} \left( \frac{1}{\sqrt{x}} \right)\ dx 4 ∫ 9 ( x 1 ) d x วิธีทำ
∫ 4 9 ( 1 x ) d x = ∫ 4 9 x − 1 2 d x = [ x − 1 2 + 1 − 1 2 + 1 ] 4 9 = [ x 1 2 1 2 ] 4 9 = [ 2 x 1 2 ] 4 9 = [ 2 x ] 4 9 = 2 9 − 2 4 = 2 ( 3 ) − 2 ( 2 ) = 6 − 4 = 2 \begin{align*} \displaystyle \int\limits_{4}^{9} \left( \frac{1}{\sqrt{x}} \right)\ dx &= \displaystyle \int\limits_{4}^{9} x^{-\frac{1}{2}}\ dx \\ &= \left[ \frac{x^{-\frac{1}{2} + 1}}{-\frac{1}{2} + 1} \right]_{4}^{9} \\ &= \left[ \frac{x^{\frac{1}{2}}}{\frac{1}{2}} \right]_{4}^{9} \\ &= \left[ 2x^{\frac{1}{2}} \right]_{4}^{9} \\ &= \left[ 2\sqrt{x} \right]_{4}^{9} \\ &= 2\sqrt{9} - 2\sqrt{4} \\ &= 2(3) - 2(2) \\ &= 6 - 4 \\ &= 2 \end{align*} 4 ∫ 9 ( x 1 ) d x = 4 ∫ 9 x − 2 1 d x = [ − 2 1 + 1 x − 2 1 + 1 ] 4 9 = [ 2 1 x 2 1 ] 4 9 = [ 2 x 2 1 ] 4 9 = [ 2 x ] 4 9 = 2 9 − 2 4 = 2 ( 3 ) − 2 ( 2 ) = 6 − 4 = 2
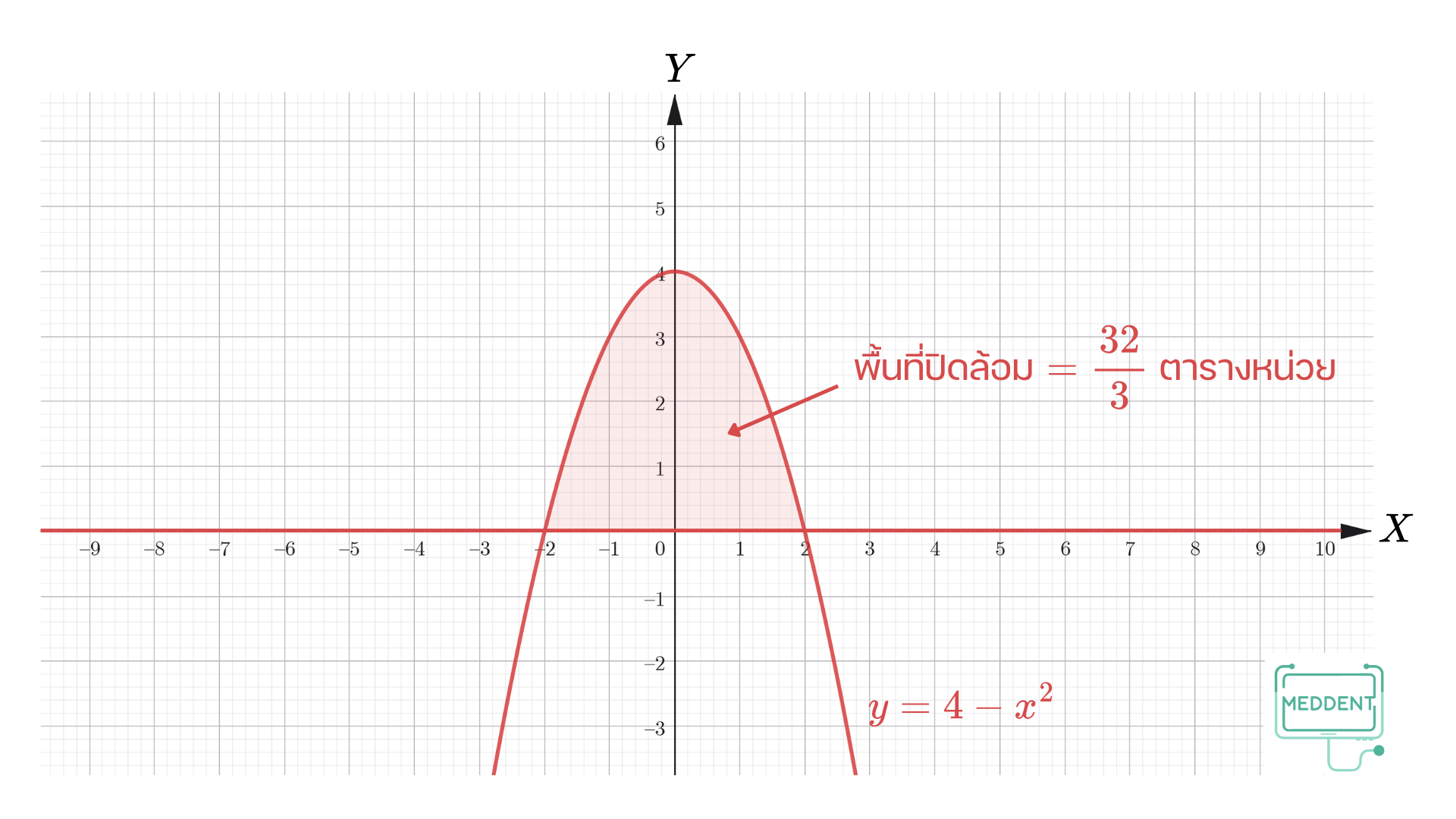
Ex. จงหาพื้นที่ปิดล้อมด้วยเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X วิธีทำ พิจารณาจุดตัดของเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X ให้ y = 0 y=0 y = 0
0 = 4 − x 2 0 = ( 2 − x ) ( 2 + x ) x = 2 , − 2 \begin{align*} 0 &= 4 - x^2\\ 0 &= (2-x)(2+x)\\ x &= 2, -2 \end{align*} 0 0 x = 4 − x 2 = ( 2 − x ) ( 2 + x ) = 2 , − 2
ดังนั้น จุดตัดของเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X ( 2 , 0 ) (2,0) ( 2 , 0 ) ( − 2 , 0 ) (-2,0) ( − 2 , 0 )
ต่อไปจะหาพื้นที่ปิดล้อมด้วยเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X เนื่องจากเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 ( 0 , 4 ) (0,4) ( 0 , 4 ) y ≥ 0 y \geq 0 y ≥ 0 x ∈ [ − 2 , 2 ] x\in [-2,2] x ∈ [ − 2 , 2 ] จะได้ว่า พื้นที่ปิดล้อมด้วยเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X
∫ − 2 2 ( 4 − x 2 ) d x = [ 4 x − x 3 3 ] − 2 2 = ( 4 ( 2 ) − 2 3 3 ) − ( 4 ( − 2 ) − ( − 2 ) 3 3 ) = ( 8 − 8 3 ) − ( − 8 + 8 3 ) = 8 − 8 3 + 8 − 8 3 = 16 − 16 3 = 48 − 16 3 = 32 3 \begin{align*}\displaystyle \int_{-2}^{2} (4 - x^2) dx &= \left[ 4x - \frac{x^3}{3} \right]_{-2}^{2} \\ &= \left( 4(2) - \frac{2^3}{3} \right) - \left( 4(-2) - \frac{(-2)^3}{3} \right) \\ &= \left( 8 - \frac{8}{3} \right) - \left( -8 + \frac{8}{3} \right) \\ &= 8 - \frac{8}{3} + 8 - \frac{8}{3} \\ &= 16 - \frac{16}{3} \\ &= \frac{48 - 16}{3} \\ &= \frac{32}{3} \end{align*} ∫ − 2 2 ( 4 − x 2 ) d x = [ 4 x − 3 x 3 ] − 2 2 = ( 4 ( 2 ) − 3 2 3 ) − ( 4 ( − 2 ) − 3 ( − 2 ) 3 ) = ( 8 − 3 8 ) − ( − 8 + 3 8 ) = 8 − 3 8 + 8 − 3 8 = 16 − 3 16 = 3 48 − 16 = 3 32
ดังนั้น พื้นที่ปิดล้อมด้วยเส้นโค้ง y = 4 − x 2 y = 4 - x^2 y = 4 − x 2 X X X 32 3 \displaystyle\frac{32}{3} 3 32
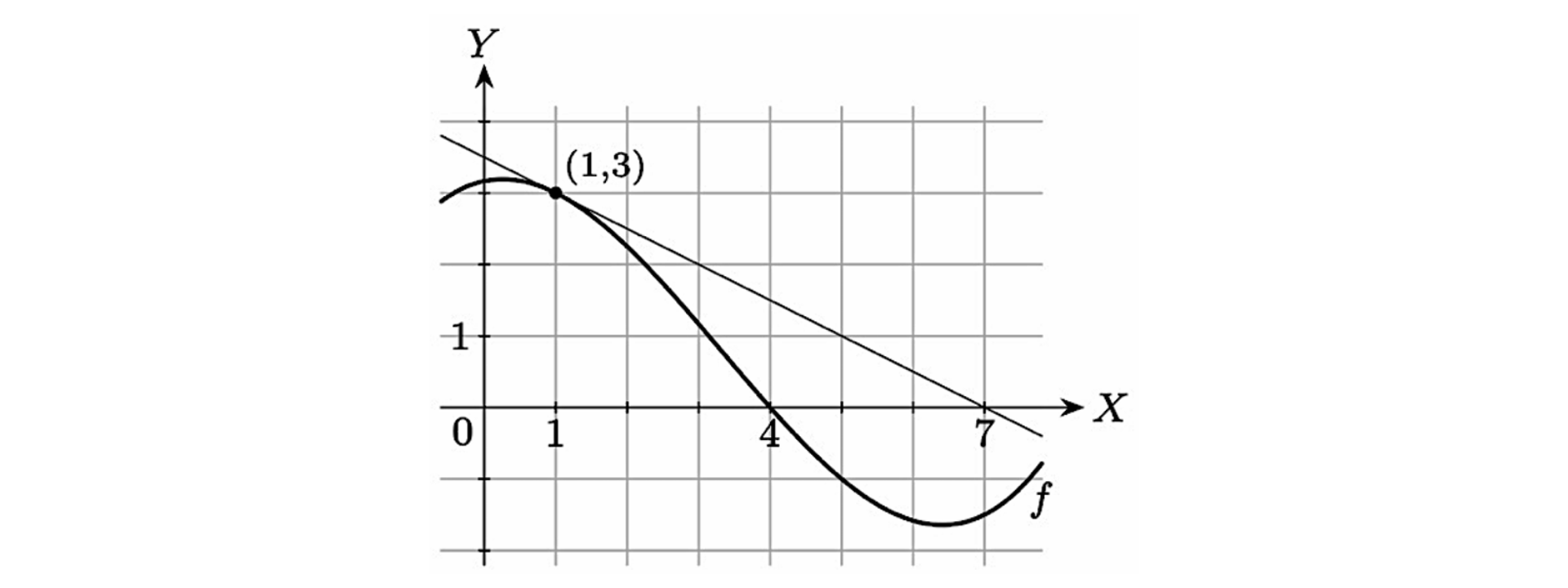
ให้ f f f x = 1 x = 1 x = 1
ค่าของ f ′ ( 1 ) f'(1) f ′ ( 1 )
− 3 -3 − 3 − 2 -2 − 2 − 1 2 -\displaystyle\frac{1}{2} − 2 1 1 2 \displaystyle\frac{1}{2} 2 1 3 3 3 วิธีทำ กำหนดให้ ℓ \ell ℓ ( 1 , 3 ) (1,3) ( 1 , 3 ) f f f x = 1 x = 1 x = 1 ซึ่งทำให้สามารถหาค่าของ f ′ ( 1 ) f'(1) f ′ ( 1 ) ℓ \ell ℓ
m = y 2 − y 1 x 2 − x 1 = 0 − 3 7 − 1 = − 3 6 = − 1 2 \begin{align*} m&=\displaystyle\frac{y_2-y_1}{x_2-x_1} \\ &=\displaystyle\frac{0-3}{7-1}\\ &= -\displaystyle\frac{3}{6}\\ &= -\displaystyle\frac{1}{2}\\ \end{align*} m = x 2 − x 1 y 2 − y 1 = 7 − 1 0 − 3 = − 6 3 = − 2 1
ตอบ ข้อ 3. − 1 2 -\displaystyle\frac{1}{2} − 2 1